Endlich so denken wie Einstein! Die erfolgreiche Messung von Gravitationswellen öffnet ein neues Fenster zum Universum

„Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden gewachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund an sollen ,Raum an sich’ und ,Zeit für sich’ völlig zu Schatten herabsinken, und nur noch eine Union der beiden soll Selbständigkeit bewahren.”¹

Pünktlich zum Untergang des bankrotten Finanzsystems tut sich der Menschheit ein neues Paradigma auf – weg vom „Jeder-gegen-Jeden”-Denken und „Koste-es-was-es-wolle”-Jagen nach immer größerem Profit, hin zu einer weisen Politik des allgemeinen Nutzens für die Menschheit und des wiedererwachten Staunens über die eigene Fähigkeit, dieses unfaßbare unendlich paradoxe Universum immer besser begreifen zu können.

Dieses neue Paradigma hat sich schon lange angekündigt, z. B. mit Entdeckungen des Gravitationsfeldes der Erde durch Gravity Probe 2011, entscheidenden Durchbrüchen in Fusionsforschung und Plasmaphysik, dem Gelingen des XFel-Lasers oder dem Projekt der Chinesen, die Rückseite des Mondes zu erforschen. Und nun die große Sensation: Die erfolgreiche Messung der Gravitationswellen, die am 14. September 2015 um 5:51 Uhr US-Ostküstenzeit von beiden identischen Laser Interferometer Gravitational-wave Observatory (LIGO)-Detektoren in Livingston (Louisiana) und Hanford (Washington) in den USA registriert wurden. Sie bestätigen aufs Neue die von Albert Einstein in seiner Allgemeinen Relativitätstheorie 1915 vorhergesagte Krümmung der Raum-Zeit.

Die Entdeckung gibt den Wahrheitssuchern aus Astronomie und Weltraumfahrt ungeahnten Auftrieb und kann uns wieder zu Renaissance-Menschen machen, denn so paradox es vielleicht klingen mag: das Universum hilft uns, wenn wir uns aufmachen, es wahrhaft zu erforschen, wie es Friedrich Schiller in seinem Gedicht „Kolumbus” treffend beschrieb:

„… Dort muß die Küste sich zeigen,
Liegt sie doch deutlich und liegt schimmernd vor deinem Verstand.
Traue dem leitenden Gott und folge dem schweigenden Weltmeer,
Wär sie noch nicht, sie stieg‘ jetzt aus den Fluten empor.
Mit dem Genius steht die Natur in ewigem Bunde,
Was der eine verspricht, leistet die andre gewiß.”

Vor über 100 Jahren hatte Albert Einstein in einer Sitzung der Akademie der Wissenschaften zu Berlin seine bahnbrechenden Postulate zur Allgemeinen Relativitätstheorie vorgestellt und damit die ganze Newtonsche Physik über den Haufen geworfen. Nach seiner Theorie werden die Bahnen der Himmelskörper nicht durch „Kräfte” bestimmt, sondern ihre Massen verändern die Geometrie des Raumes. Man könnte auch sagen, die Gravitation ist eine geometrische Kraft. Das Gravitationsfeld ist durch die Konfiguration von Massen bestimmt und wechselt mit diesen beständig, daher ist die geometrische Struktur des Raumes von diesen physikalischen Faktoren abhängig. Einstein sagte:

„Die Geometrie des Raumes wird durch die Massen bestimmt… Der Raum ist also gemäß dieser Theorie – genau wie es Riemann geahnt hat – kein absoluter mehr, sondern seine Struktur hängt von physikalischen Einflüssen ab. Die (physikalische) Geometrie ist keine isolierte, in sich geschlossene Wissenschaft mehr wie die Geometrie Euklids.”²

War die Welt bereit für ein völliges Umdenken bezüglich des Raumes und der Zeit? Einstein wurde bejubelt, bewundert und bestaunt, aber hatte man die ganze Tragweite seiner Entdeckung verstanden?

Herausragend ist, daß Einstein nicht irgendwelche Formeln präsentierte und sagte: Hier, so funktioniert das Universum. Nein, Einstein machte viele und bedeutende astronomische Voraussagen, denn wie sein großes Vorbild Kepler stand er mitten im realen physikalischen Geschehen. Für ihn stand die physikalische Welt an erster Stelle, die Mathematik war ein notwendiges Hilfswerkzeug, das – wenn nötig – geändert werden muß.

So überlegte er bei der Erklärung seiner Allgemeinen Relativitätstheorie, daß durch die Massen der Himmelskörper auch notwendigerweise die Geschwindigkeit der Lichtstrahlen verändert wird. Denn wenn man von zwei Bezugssystemen aus – einem ruhenden K und einem beschleunigten K’ – einen Lichtstrahl beobachtet, so pflanzt sich dieser für den ruhenden Beobachter in gerader Linie (luftleerer Weltraum) fort; für den Beobachter im beschleunigten System aber ist die Bahn desselben Lichtstrahles keine Gerade mehr:

„Hieraus ist zu schließen, daß sich Lichtstrahlen in Gravitationsfeldern im allgemeinen krummlinig fortpflanzen.”³

Diese Beschleunigung, die sich auf alle vom ruhenden System aus geradlinig erscheinende Bewegungen auswirkt, so daß sie krummlinig aussehen, entspricht dem Einfluß des relativ zu K’ herrschenden Gravitationsfeldes auf den bewegten Körper, also die Teile des Lichtstrahls.

Während diese Krümmung der Lichtstrahlen für die uns betreffenden Gravitationsfelder gering ist, berechnete Einstein, daß sie für Lichtstrahlen, die in der Nähe der Sonne vorbeigehen, doch 1,7 Bogensekunden betragen muß:

„Dies müßte sich dadurch äußern, daß die in der Nähe der Sonne erscheinenden Fixsterne, welche bei totalen Sonnenfinsternissen der Beobachtung zugänglich sind, um diesen Betrag von der Sonne weggerückt erscheinen müssen gegenüber der Lage, die sie für uns am Himmel annehmen, wenn die Sonne an einer anderen Stelle am Himmel steht. Die Prüfung des Zutreffens oder Nichtzutreffens dieser Konsequenz ist eine Aufgabe von höchster Wichtigkeit, deren baldige Lösung wir von den Astronomen erhoffen dürfen.”⁴

Diese Hypothese machte Einstein im Jahre 1913. Und tatsächlich wurde die Existenz der von der Theorie geforderten Lichtablenkung von dem englischen Astronomen Eddington bei der Sonnenfinsternis vom 30. Mai 1919 photographisch festgestellt. Für das Jahr 1919 erwartete man eine Sonnenfinsternis, die für das Experiment sehr geeignet war, da sich die Sonne zur Zeit der Verfinsterung inmitten einer Anzahl besonders heller Fixsterne, der Hyoden, befand, die als Lichtquellen genutzt werden konnten. Die wissenschaftliche Welt wartete mit Spannung auf die Messung, die natürlich Einsteins Vorhersage voll und ganz bestätigte. Die Ablenkung war sogar doppelt so groß, wie sie nach dem Newtonschen Gesetz zu erwarten gewesen wäre. Das war der Beweis für die Raumkrümmung.

Als Einstein die Mitteilung erhielt, bemerkte er: „Ich wußte, daß die Theorie richtig ist. Haben Sie daran gezweifelt?” Die Besucherin erwiderte: „Nein, natürlich nicht. Doch was hätten Sie gesagt, wenn die Bestätigung nicht so ausgefallen wäre?”, worauf Einstein antwortete: „Da könnt’ mir halt der liebe Gott leid tun, die Theorie stimmt doch.”⁵

Tatsächlich hatte niemand an diese Sensation wirklich geglaubt. Man hatte sich geistig mit dem Newtonschen Gesetz gemütlich zur Ruhe gesetzt. Doch damit war es jetzt vorbei!

Zuerst einmal überschlug sich die sensationshungrige Welt; überall erschienen Artikel über Einstein und die „Relativität”, man riß sich um Termine mit dem berühmten Mann. Seine zweite Frau Elsa berichtete in einem Brief an einen gemeinsamen Freund über die Aufnahme in Japan:

„Es wurde ihnen eine Flucht von Zimmern im ersten Hotel Tokios zugewiesen, mit einem großen Balkon, der den Blick auf einen öffentlichen Platz freigab. Dort saßen die Leute schon in der Nacht auf mitgebrachten Stühlen, um den großen Mann bald zu Gesicht zu bekommen. Endlich erschien er auf dem Balkon; einen Schritt hinter ihm stand seine Frau Elsa. Es gab orkanartiges Gebrüll zur Begrüßung, und Einstein verbeugte sich lächelnd. Er war überwältigt und flüsterte: ,Elsa, ich glaube kaum, daß einem lebenden Menschen so viel Ehre zukommen kann.‘ Dann aber sagte er, immer noch lächelnd und sich verbeugend: ,Elsa, ich fürchte, daß wir noch im Zuchthaus enden.‘”⁶

Doch Einstein ging es im Gegensatz zu Newton überhaupt nicht um persönlichen Ruhm. Die Tatsache, daß er mit seiner Allgemeinen Relativitätstheorie nicht nur Newtons Mechanik überflüssig machte, sondern auch seine eigene spezielle Relativitätstheorie zu einem Grenzfall degradierte, beweist seine herausragende Geistesgröße und Charakterstärke, die ihn mit einigen Ausnahmen vor allen Wissenschaftlern auszeichnet. Es ging ihm einfach um das bessere Verständnis der Naturprinzipien:

„Da die Gegner der Relativitätstheorie öfters behauptet haben, die spezielle Relativitätstheorie werde durch die allgemeine Relativitätstheorie über den Haufen geworfen, will ich den wirklichen Sachverhalt durch einen Vergleich deutlich machen… Es ist das schönste Los einer physikalischen Theorie, wenn sie selbst zur Aufstellung einer umfassenderen Theorie den Weg weist, in welcher sie als Grenzfall weiterlebt.”⁷

Wenn man sich dagegen das Lamentieren der Newton-Anhänger bis auf den heutigen Tag anhört, so sieht man, wie bemitleidenswert klein sie doch sind. Hundert Jahre sind nun vergangen, in denen man in den Schulen immer noch von „Anziehungs- und Abstoßungskräften” der Massen hört, die durch die Aufstellung des Newtonschen Bewegungsgesetzes erfunden werden mußten.

Deshalb ist die Messung von Gravitationswellen im September 2015 von großer Bedeutung für die Wissenschaft und auch für unser allgemeines Verständnis von der Welt. Jetzt, 100 Jahre nach Einsteins Entdeckung, sind wir vielleicht endlich bereit für seine großen Ideen, denn wir wollen ja nicht, daß man heute noch wie damals Charlie Chaplin bei einer gemeinsamen Autofahrt, wo beide von den Menschen bejubelt wurden, erklären kann: „Die Leute feiern Sie, weil keiner Sie verstanden hat – und mich, weil jeder mich versteht.”⁸

Das Geoid wackelt!

Was ist eigentlich der Raum? Wie kann man sich die Geometrie eines Gravitationsraumes vorstellen? Tatsächlich war es erst mit der Entwicklung besserer Teleskope möglich, genauere Einblicke in den Weltraum zu erlangen. Eine ganz besondere Bedeutung hatte hierbei die Installation des Weltraumteleskops Hubble, wie es der damalige Direktor des Space Telescope Science Institute in Baltimore, Maryland, Robert Williams, ausdrückte:

„In den letzten Jahren zeigte sich, daß die irdische Atmosphäre den begrenzenden Faktor in unserem Bemühen darstellt, die allerfeinsten Strukturen in astronomischen Objekten zu kennen. Dies ist der Grund, warum die Astronomen darauf drängten, Teleskope in eine Erdumlaufbahn zu bringen, wo sie von der irdischen Atmosphäre ungestört die Tiefen des Weltraums erforschen können… Der Beginn des bemannten Raumfahrtprogramms der NASA mit seinen regelmäßigen Shuttle-Flügen war für das Projekt des Weltraumteleskops Voraussetzung und Startschuß zugleich… Die einzigartigen Möglichkeiten eines erdumkreisenden Weltraumteleskops mit seinen Zusatzgeräten stellen einen technologischen Fortschritt gegenüber den früheren Teleskopen dar, und dies hat schon zu bedeutenden Entdeckungen geführt: Hubble beobachtete den dramatischen Einschlag eines großen Kometen auf Jupiter, die seltsamen Explosionen sterbender Sterne und die geheimnisvollen Bewohner der Zentren großer Galaxien, die massereichen Schwarzen Löcher…”⁹

Aber auch die Entwicklung der Lasertechnologie in den 1960er Jahren – deren Prinzip übrigens von Einstein in seinem 1916 erschienenen Papier „Zur Quantentheorie der Strahlung” ebenfalls vorausgesagt worden ist – machte es rein technisch überhaupt erst möglich, internationale Großprojekte wie LIGO oder das GEO in Hannover durchzuführen. Dabei geht das Verständnis oft Hand in Hand mit den technologischen Entwicklungen. So wußte man zwar schon seit 1919, daß große Massen das Licht tatsächlich ablenken, doch erst viel später machte man die Entdeckung, daß diese dann auch wie riesige Linsen wirken. So entdeckte man im Jahre 1985 das sog. „Einsteinkreuz”, ein Gravitationslinsensystem im Sternbild Pegasus (Abbildung 1).

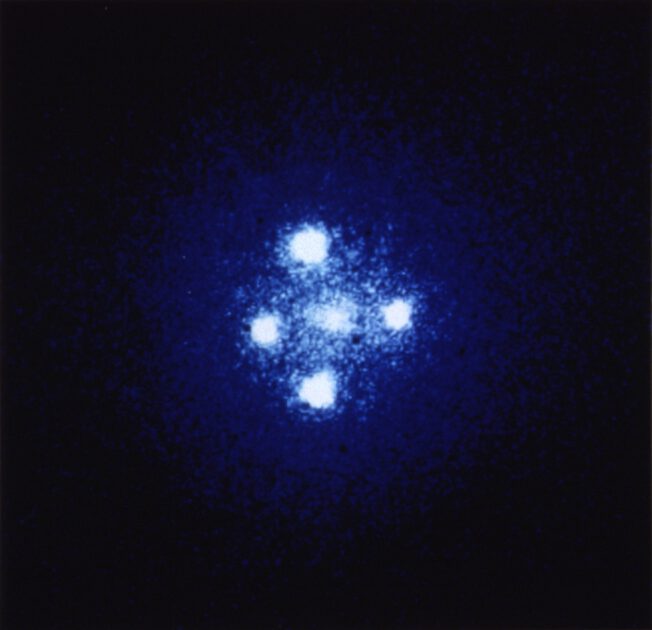
Es wurden außerdem Phänomene entdeckt, die man sich nur durch die Konzentration riesiger Punktmassen, wie sie Schwarzfield aus Einsteins Allgemeiner Relativitätstheorie geschlossen hatte, erklären konnte: riesige Massezentren, die Raum und Zeit extrem krümmen und um die mehrere Planeten wie um eine große Sonne kreisen – nur daß da keine Sonne ist. Der amerikanische Physiker John Wheeler bezeichnete 1969 als erster diese Kollapsare oder sogenannten „Gefrorenen Sterne”, die auf einen winzigen, aber enorm großen Massepunkt zusammengeschrumpft sind, als

„Schwarze Löcher”.

Mit dem Nachweis der Gravitationswellen versprechen sich die Forscher nun eine Entwicklung noch genauerer Meßmethoden, die solche Phänomene untersuchen und vielleicht bestätigen, ob sie einen echten physikalischen Hintergrund haben. Auf jeden Fall ergibt sich dadurch ein ganz neuer Zugang zum Universum! Prof. Karsten Danzmann, Leiter der Abteilung für Gravitationswellen-Astronomie am Albert-Einstein-Institut (AEI) in Hannover, der am Detektor GEO600 die Suche nach den Gravitationswellen anführt, erklärte das so:

„Man kann das Universum so nicht nur sehen, sondern auch hören…” und: „Jetzt fängt es erst an. Wir werden noch viele solche Signale sehen; wir haben ein ganz neues Fenster ins Universum, wir können viel über die Dunkle Energie und die Entstehung von Galaxien lernen. Die Kollision dieser beiden Schwarzen Löcher war das gewaltigste Ereignis, das je beobachtet wurde; in Sekundenbruchteilen wurden mehrere Sonnenmassen verbrannt und in Strahlung umgewandelt. Und trotzdem hat nach meiner Kenntnis kein elektromagnetisches Teleskop etwas gemessen, es blieb völlig dunkel. Zu dieser Schattenwelt haben wir jetzt Zugang. Denn über 99 Prozent des Universums sind dunkel und strahlen keine elektromagnetischen Wellen aus, aber alles unterliegt der Schwerkraft.”¹⁰

Es geht hier nicht um eine neue Art von Strahlung, die jetzt entdeckt wurde, oder Wellen, die sich nur beim Verschmelzen von schwarzen Löchern oder gewaltigen Sternexplosionen im Weltraum ausbreiten. Hier geht es um eine geometrische Charakteristik unseres Universums, in welchem sich die Himmelskörper wie in einem ständig und überall vielfältig gekrümmten Feld bewegen. Und das ist immer so, Einstein hat es herausgefunden, und diese geometrischen Schwingungen haben wir jetzt mit Hilfe unserer weiterentwickelten technischen Möglichkeiten gemessen.

Man muß sich das so vorstellen: durch das ständige Geruckel und Gezerre aufgrund des Einflusses großer Massen in der Milchstraße – in ihrem Zentrum befindet sich ein Schwarzes Loch von allein 4,31 Millionen Sonnenmassen – wackelt unser Geoid unregelmäßig in jedem kleinsten Punkt seiner Bahn in einer Delle des Schwerefeldes der Sonnen (Abbildung 2).

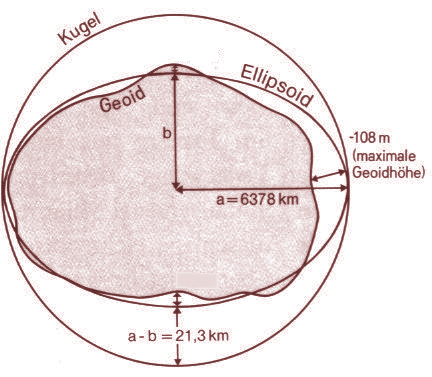
Es geht also um eine geometrische Eigenschaft des Raumes, die genau genommen vierdimensional ist, und das kann man nur begreifen, wenn man seine Vorstellungskraft vergrößert, so wie wir Menschen es ganz natürlich immer machen, wenn wir physikalische Phänomene begreifen und bildhaft machen wollen.

Einstein selber hat bewußt die reale physikalische Welt vor die Mathematik gestellt, und nur deshalb konnte er seine Entdeckungen machten. Sein Geist war frei von festgelegten „Annahmen” über die Naturvorgänge – im Gegensatz zu fast allen Wissenschaftlern bis heute.

Die Möglichkeit, sich das ganze geometrisch vorzustellen, hat eine lange Geschichte, die mit Johannes Kepler anfing, durch Gauß und Riemann weitergeführt und von Einstein vollendet wurde: die Betrachtung aller möglichen Funktionen, die durch Kegelschnitte erzeugt werden, die höhere projektive Geometrie, mit der Gauß bereits im Alter von 19 Jahren mit nur drei Bahndaten die Bahn des Asteroiden Ceres fand, sowie die komplexen Funktionen und die Riemannsche Geometrie.

War Einstein ein Zauberer?

Wie kam Einstein eigentlich auf all diese umwerfenden Ideen und Vorhersagen? War er ein Zauberer? Konnte er die Zukunft vorhersagen? Wenn man sich näher mit dieser Frage befaßt, so sieht man, daß Einstein im Gegensatz zu Newton, der mit mystischen, willkürlichen Annahmen seine Gravitationstheorie akzeptabel machen wollte, mit seiner Theorie endlich Klarheit in die ganze Sache brachte. Seine Voraussagen waren einfach die Schlußfolgerungen aus seiner Theorie.

Einstein war schon als 16jähriger stutzig geworden über die Tatsache, daß alles, ganz gleich, was man fallen läßt – eine Stahlkugel oder einen Radiergummi – mit der gleichen Schnelligkeit zu Boden fällt, wenn man von der Reibung absieht. Das Phänomen beschäftigte ihn stark, und er kam zu dem Schluß, daß demnach bei fallenden Gegenständen auf der Erde etwas anderes wirken müßte als das, was man normalerweise mit Newton als „Erdanziehung” bezeichnete:

„Das Gravitationsfeld weist im Gegensatz zum elektrischen und magnetischen Felde eine höchst merkwürdige Eigenschaft auf, welche für das Folgende von fundamentaler Bedeutung ist. Körper, die sich unter ausschließlicher Wirkung des Schwerefeldes bewegen, erfahren eine Beschleunigung, welche weder vom Material, noch vom physikalischen Zustande des Körpers im geringsten abhängt.”¹¹

Das bedeutete, daß die träge und die schwere Masse eines Körpers gleich waren.

„Die bisherige Mechanik hat diesen wichtigen Satz zwar registriert, aber nicht interpretiert. Eine befriedigende Interpretation kann nur so zustande kommen, daß man einsieht: Dieselbe Qualität des Körpers äußert sich je nach Umständen als ,Trägheit‘ oder als ,Schwere‘.”⁴

Kein Physiker hatte bis dahin darüber nachgedacht, daß ein Bewegungsgesetz doch alle Phänomene erklären, d. h. einen Grund haben müßte. Daraufhin begann sich Einstein eingehend mit der bisherigen „anerkannten Mechanik” zu beschäftigen, und er erkannte, daß in dieser „Newtonschen Mechanik” die „Realität” auf zwei völlig willkürlichen Annahmen über den absoluten Raum und die absolute Zeit basierte:

„Die relative, scheinbare und gewöhnliche Zeit ist ein fühlbares und äußerliches, entweder genaues oder ungleiches Maß der Dauer, dessen man sich gewöhnlich statt der wahren Zeit bedient, wie Stunde, Tag, Monat und Jahr.”

Und:

„Der absolute Raum bleibt vermöge seiner Natur und ohne Beziehung auf einen äußeren Gegenstand stets gleich und unbeweglich.”

Dieser fast mystische Glaube blieb lange in der Physik erhalten:

„Und doch blieb der Raum im Bewußtsein der Physiker bis in die jüngste Zeit ausschließlich das passive Gefäß allen Geschehens, das am physikalischen Geschehen selbst keinen Anteil hatte… Da es den Physikern des 19. Jahrhunderts völlig absurd erschienen wäre, dem Raum selbst physikalische Funktionen bzw. Zustände zuzuschreiben, so konstruierte man sich ein den ganzen Raum durchdringendes Medium, den Äther, nach dem Modell der ponderablen Materie, das Träger der elektromagnetischen und damit auch der Lichtvorgänge sein sollte…”

und:

„In der Physik herrschte bei aller Fruchtbarkeit im Einzelnen in prinzipiellen Dingen dogmatische Starrheit: Am Anfang – wenn es einen solchen gab – schuf Gott Newtons Bewegungsgesetze samt den notwendigen Maßen und Kräften. Das ist alles; das Weitere ergibt die Ausbildung geeigneter mathematischer Methoden durch Deduktion… Wir dürfen uns daher nicht wundern, daß sozusagen alle Physiker des letzten Jahrhunderts in der klassischen Mechanik eine feste und endgültige Grundlage der ganzen Physik, ja, der ganzen Naturwissenschaft sahen, und daß sie nicht müde wurden, zu versuchen, auch die indessen langsam sich durchsetzende Maxwellsche Theorie des Elektromagnetismus auf die Mechanik zu gründen.”¹²

Einstein war ein großer Verehrer von Johannes Kepler und wußte von diesem, daß es immer erst darum gehen müßte, sich eine Vorstellung vom Raum zu machen. Und ähnlich wie Kepler dachte er vollkommen vorurteilslos, oder besser gesagt, er wußte wie jener, daß man sich ständig hinterfragen mußte, welche Vorstellungen man voraussetzen dürfte und welche nicht.

„Wenn ich ohne schwere Bedenken und eingehende Erläuterungen die Aufgabe der Mechanik so formuliere ,Die Mechanik hat zu beschreiben, wie die Körper mit der Zeit ihren Ort im Raume ändern‘, so nehme ich einige Todsünden gegen den heiligen Geist der Klarheit auf mein Gewissen; diese Sünden sollen zunächst aufgedeckt werden… Es ist unklar, was hier unter ,Ort‘ und ,Raum‘ zu verstehen ist…”¹¹

Einstein beschäftigte sich außerdem eingehend mit Gauß und Riemann, und genau wie diesen war ihm bewußt, daß es höchst naiv sei, alle Vorgänge in unserem Universum in einer dreidimensionalen Geometrie erklären zu wollen. Obwohl Gauß selber an der Aufstellung einer antieuklidischen Geometrie arbeitete, hatte erst Bernhard Riemann als erster gewagt, die umwälzenden Gedanken einer anderen Geometrie 1854 in seiner Antrittsvorlesung öffentlich vorzutragen:

„Bekanntlich setzt die Geometrie sowohl den Begriff des Raumes, als die ersten Grundbegriffe für die Konstruktionen im Raume als etwas Gegebenes voraus. Sie gibt von ihnen nur Nominaldefinitionen, während die wesentlichen Bestimmungen in Form von Axiomen auftreten. Das Verhältnis dieser Voraussetzungen bleibt dabei im Dunkeln; man sieht weder ein, ob und in wie weit ihre Verbindung notwendig, noch a priori, ob sie möglich ist. Diese Dunkelheit wurde auch von Euklid bis auf Legendre, um den berühmtesten neueren Bearbeiter der Geometrie zu nennen, weder von den Mathematikern, noch von den Philosophen, welche sich damit beschäftigten, gehoben…”¹³

Riemann hatte als erster deutlich ausgesprochen, daß die Frage nach der Geometrie die Basis für das Verständnis aller Naturbeschreibung ist. Damit stellte sich auch die Frage: Was ist eigentlich der Raum? Wenn unser Universum kein dreidimensionaler Kasten ist, wie sollen wir ihn uns vorstellen?

Was ist der Raum?

Schon durch die Pythagoräer und danach durch Nikolaus von Kues und durch Keplers Entdeckung der gesetzmäßigen Verhältnisse der Bewegungen in unserem Sonnensystem hatte sich ein tiefes Verständnis über die Geometrie des Raumes entwickelt. Keplers Untersuchung der Unregelmäßigkeiten der Planetenbahnen, seine Überlegungen über die Kegelschnitte, Leibniz’ und Bernoullis Untersuchung der Kettenlinie, Gauß’ und Riemanns Entwicklung der projektiven Geometrie und ihre Gedanken über eine „antieuklidische Geometrie” hatten eine Revolution in Gang gesetzt, die Einsteins Entdeckungen den Weg ebneten. Allerdings erreichte diese geometrische Revolution nie die allgemeinen Lehrbücher.

Die entscheidende Frage: Was ist der Raum? Was bestimmt seine Geometrie?, ist uralt. Pythagoras wußte schon vor ca. 2500 Jahren, daß eine direkte Wechselwirkung des menschlichen Geistes mit dem physischen Universum durch die Erschaffung von Zahlen entsteht. Der menschliche Geist drückt dadurch seine Konzepte aus, die er über die Prinzipien der Natur herausfindet. Diese benutzt er, um weitere Untersuchungen über die Beziehungen untereinander zu machen. Dabei haben die Zahlen selber zwar keine eigene physikalische Kraft, doch sie sind Abbilder der im Universum wirkenden Prinzipien. Hinter den Zahlen stecken also echte physikalische Prinzipien, und Pythagoras sagt, daß alle Dinge kraft der Zahlen durch den menschlichen Geist erkannt und verstanden werden können.

Mit Hilfe der ganzen Zahlen drücken wir die meisten einfachen Zusammenhänge und Verhältnisse aus, sie entsprechen unserer dreidimensionalen Vorstellung des Raumes.

Damit kennen wir aber auch die „irrationalen” Zahlen, die uns schon mehr in Verwunderung versetzen. Dieser Begriff wurde eingeführt, um davon abzulenken, daß hinter diesen Zahlen ein Erzeugungsprinzip des Kreises steckt, das schon Pythagoras als „Inkommensurabilität” beschrieben hatte. Nikolaus von Kues zeigte dann in seiner Schrift De circuli quadratura, daß unser Geist diese Zahl als Ausdruck eines physikalischen Prozesses zwar klar vor Augen hat, doch der rechnerische Verstand hinter dem Erkennen des Geistes zurückbleibt:

„Dies überschreitet aber alle unsere Vernunft, die in ihrem Ursprung die Widersprüche nicht auf dem Wege des Denkens vereinigen kann, da wir nur durch das, was uns von Natur einsichtig ist, voranschreiten. Unsere Vernunft aber bleibt weit hinter diesem unendlichen Vermögen zurück und kann daher die unendlich weit voneinander abstehenden Glieder des Widerspruchs nicht verbinden…”¹⁴

Am besten läßt sich dies an der Frage der Verdoppelung des Quadrates veranschaulichen. Betrachten wir uns das Verhältnis 1 : 2, das bei diesem Prozeß entsteht. Wenn man aus einem Kreis ein Quadrat erzeugt, indem man ihn zweimal im Mittelpunkt so faltet, daß die zweite Falte genau senkrecht auf der ersten steht, und dann die Schnittpunkte der Falten mit dem Umfang untereinander verbindet, so erhält man das Quadrat (Abbildung 3 a).

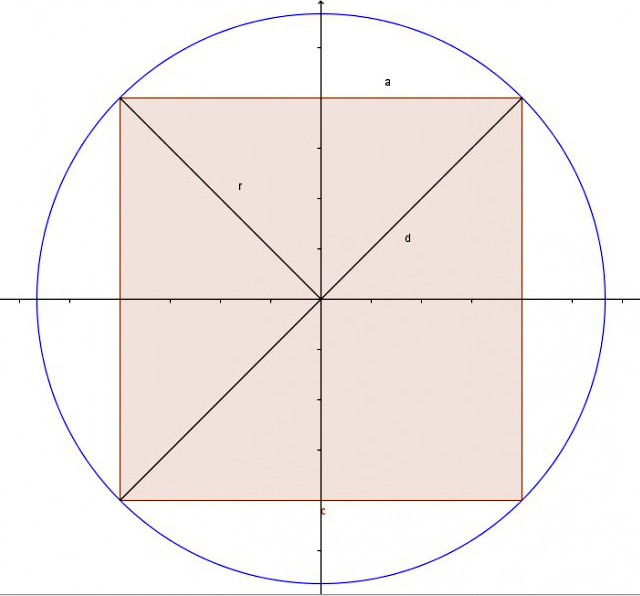
Im Menon-Dialog beschreibt Platon nun den Vorgang der Verdoppelung dieses Quadrates, dessen Seiten a wir einfach als 1 annehmen. Er vergleicht dabei die Diagonale des erzeugten Quadrates mit einer seiner Seiten und zeigt, daß es ein ganz einfach scheinendes Verhältnis besitzt: nämlich 1 : 2 (Abbildung 3 b):

Nach dem Satz des Pythagoras ist

1. a² + b² = c² , wobei wir hier die Diagonale c nennen. Da hier b genauso wie a gleich 1 ist, haben wir:
2. 12 + 12 = c² , also:
3. 2 = c²

c ist also die Quadratwurzel aus zwei! Das bedeutet aber, daß, wenn man c als Seite eines neuen Quadrates nimmt, dieses genau doppelt so groß ist wie das erste. Die Seiten beider Quadrate stehen aber in einem inkommensurablen Verhältnis zueinander.

Auf diese Weise versuchen wir uns eine immer klarere Vorstellung von der Gestalt der physischen Vorgänge zu machen. Ein Beispiel, wie man dies üben kann bzw. seinen Geist daran gewöhnen kann, sich den Raum vorzustellen, zeigt eine Anekdote von einem Schüler des Berner Mathematikers Jacob Steiner, den Alexander von Humboldt zusammen mit Dirichlet an die Berliner Akademie holte. Jacob Steiner wurde bedeutend in der projektiven Geometrie im Sinne von Carl Friedrich Gauß:

„Er hatte die Frage aufgeworfen, wieviel Kugeln um ein vollständiges Tetraeder umschrieben werden könnten, und als wir zu überlegen, vielleicht auch zu raten anfingen, da erging er sich erst in einigen Anzüglichkeiten und fuhr dann in seinem Schweizerdeutsch fort: ,Als ich so ein kleines Hirtenbüble war und so vor mich hinschaute, da sah ich so eine Ebene, so eine Ebene (und damit fuhr er mit der Hand durch den Raum), und die teilte den ganzen Raum so in zwei Teile, daß ich von dem einen nicht in den anderen hinein konnte, ich mußte durch die Ebene hindurch. Und dann nahm ich eine zweite Ebene hinzu, eine zweite Ebene (wieder die entsprechende Handbewegung), und da hatte ich vier solche Teile des Raumes‘ usw. So fuhr er fort, erst eine dritte und dann eine vierte Ebene hinzuzunehmen, immer mit der Hand und mit den Augen die einzelnen Teilungen begleitend, bis wir das abgeschlossene Tetraeder vor uns sahen und die daran anstoßenden, an drei oder vier Ebenen angrenzenden Räume und die sie berührenden Kugeln. ,So‘, sagte er, ,sehe ich alle geometrischen Sätze, das Beweisen kommt nachher‘.”¹⁵

Gibt es denn auch Zahlen, die uns Zugang zu der von Einstein postulierten vierdimensionalen Raum-Zeit geben können? Erreichen wir hier nicht die Grenzen unserer Vorstellungskraft? Man braucht nur etwas Mut, um sich ins Vierdimensionale zu begeben – unsere menschliche Vorstellungskraft wird uns sicher nicht im Stich lassen, denn wie schon Nikolaus von Kues in Über den Beryll (De Beryllo) sagt:

„Ferner mußt Du Dir den Satz des Protagoras merken, daß der Mensch das Maß aller Dinge ist. Denn mit den Sinnen mißt der Mensch das sinnlich Wahrnehmbare, mit der Vernunft das Vernunftgemäße, und was über das Vernunftgemäße hinausgeht, erreicht er durch Überschreiten seiner Erkenntniskraft.”

Der „mystische Schauer” des Vierdimensionalen

„Ein mystischer Schauer ergreift den Nichtmathematiker, wenn er von ,vierdimensional’ hört, ein Gefühl, das dem vom Theatergespenst erzeugten nicht unähnlich ist. Und doch ist keine Aussage banaler als die, daß unsere gewohnte Welt ein vierdimensionales zeiträumliches Kontinuum ist.”¹⁶

So beschrieb Einstein selber seine Entdeckung der Existenz des durch Massen in Raum und Zeit gekrümmten Universums. Er führte für diese vierdimensionale Raum-Zeit die Gaußschen Koordinaten ein, bei denen jeder Punkt des Raum-Zeit-Kontinuums durch drei Koordinaten x, y, z und zusätzlich durch eine vierte, die Zeit t, dargestellt wird. Vielleicht kann man sich vorstellen, daß die uns umgebende reale Welt aus den Schnittpunkten der raum-zeitlichen Lebens- oder Existenzlinien der Dinge besteht. Der Begriff „Zeit an sich” wird dann zu einem ganz neuen Ausdruck, in dem Vergangenheit und Zukunft zusammenfallen, wenn wir uns vergegenwärtigen, daß ja die von den Wissenschaftlern gerade gemessenen Gravitationswellen von Geschehnissen stammen, welche in unserem üblichen Denken schon viele Millionen Jahre zurückliegen, doch in der Raumzeit trotzdem einen Schnittpunkt mit uns besitzen! Man könnte auch sagen, in der Raum-Zeit messen wir ein Ereignis „gleichzeitig”, obwohl es in unserem „Dreidimensionalen-plus-absoluter-Zeit”-Universum längst vorbei ist.

Dank Carl Friedrich Gauß können wir uns heute eine geometrische Vorstellung von komplexen Zahlen machen. Diese lange nur „unmöglich”, „eingebildet” oder „imaginär” genannten Zahlen wurden bereits im 16. Jahrhundert von Cardano und Bombelli in mathematischen Berechnungen benutzt. Beide hatten bereits erkannt, daß man durch Einführung einer Zahl, die mit sich selbst quadriert – 1 ergibt, Lösungen von algebraischen Gleichungen dritten Grades, also kubischen Gleichungen, finden kann.

Tatsächlich zeigte aber erst Gauß in seinem vierten Beweis des „Fundamentalsatzes der Algebra”, daß diesen mathematischen „Unmöglichkeiten” eine echte Geometrie des Raumes zugrunde liegt. Von nun an nannte er sie „komplexe Zahlen” und zeigte, daß man diese vierdimensionalen Zahlen mit Hilfe der Kreisfunktionen in einer Ebene darstellen kann. Er eröffnete uns dadurch schon lange vor Einstein eine ganz neue Welt. Gemeinsam mit Riemann entwickelte er das Gebiet der komplexen Funktionen, und heute – mit der Entdeckung Einsteins – können wir an diesen komplizierten Gebilden echte physikalische Prozesse unserer Raum-Zeit erahnen.

In seinem vierten Beweis des Fundamentalsatzes beschreibt Gauß, daß er sich mit dieser Idee der Darstellung der komplexen Zahlen einen weitreichenden Eingriff in die bisherige Euklidische Geometrie vorstellt:

„Ich werde die Beweisführung in einer der Geometrie der Lage entnommenen Einkleidung darstellen, weil jene dadurch die größte Anschaulichkeit und Einfachheit gewinnt. Im Grunde gehört aber der eigentliche Inhalt der ganzen Argumentation einem höheren, von Räumlichem unabhängigen Gebiete der allgemeinen abstrakten Größenlehre an, dessen Gegenstand die nach der Stetigkeit zusammenhängenden Größenkombinationen sind, einem Gebiete, welches zur Zeit noch wenig angebaut ist, und in welchem man sich auch nicht bewegen kann ohne eine von räumlichen Bildern entlehnte Sprache.”¹⁷

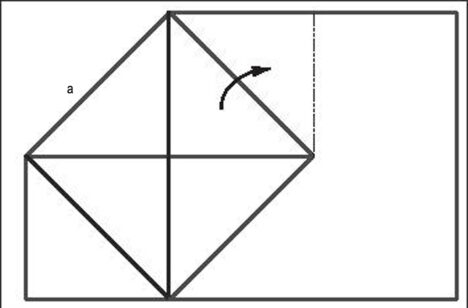
Tatsächlich kann man durch die Beschäftigung mit diesen abstrakten Gebilden unsere Raum-Zeit zu begreifen beginnen. Betrachten wir folgendes Beispiel, wie sich in einer vierdimensionalen Geometrie die Rahmenbedingungen für die Bewegung eines Körpers völlig ändern. Es handelt sich um die Konstruktion des „Doppelringes”, die der Astronom und Mathematiker A. F. Möbius (1790–1868) als Schüler von Gauß nach dessen Äußerungen überliefert hat. Möbius hatte seit dem Herbst 1813 ein Semester lang unter Leitung von Gauß auf der Göttinger Sternwarte gearbeitet. In seinen Aufzeichnungen über die krummen Flächen bezieht sich Möbius ausdrücklich auf eine mündliche Mitteilung von Gauß über die Eigenschaften eines sogenannten Doppelringes, der ihn zu dem Paradox des nach ihm benannten „Möbius-Bandes” führte:

„Man kann sich so einen Doppelring leicht zur Anschauung bringen, wenn man ein Blatt Papier in Form eines Kreuzes ausschneidet und hierauf die Enden FH und F’H’ (siehe Abbildung 4 a) des einen Paares gegenüberliegender Arme etwa oberhalb der anfänglichen Ebene des Kreuzes und die Enden BD und B’D’ des anderen Paares unterhalb dieser Ebene mit einander vereinigt. Es besitzt diese nur von einer Linie ABB’ IHH’ GD’D EF’FA begrenzte Fläche noch die merkwürdige Eigenschaft (nach einer mündlichen Mitteilung von Gauß; wodurch Gauß zur Betrachtung der Fläche geführt worden ist, ist mir unbekannt), daß man von irgend vier auf ihrem Perimeter auf einander folgenden Punkten P, Q, R, S den ersten mit dem dritten und den zweiten mit dem vierten durch zwei Linien PTT’R und QUU’S verbinden kann, welche in der Fläche selbst liegen und dennoch einander nicht schneiden – wie dies doch immer geschehen würde, wenn die Fläche eine Grundform der ersten Klasse (zum Beispiel ein Zylinder, C. H.) wäre.”¹⁸

Man kann beim Doppelring die Ähnlichkeit zum Möbius-Band (Abbildung 4 b) erkennen, denn wenn man die Streifen durch eine Linie halbiert und auf der einen Seite an einem Punkt P beginnt und vermeiden will, daß man den eigenen Weg nicht schneidet, so bewegt man sich auf dem einen Kreis außen, auf dem anderen innen, d. h. man wechselt ständig die Richtung, weshalb solche Flächen auch „nichtorientierbar” genannt werden.

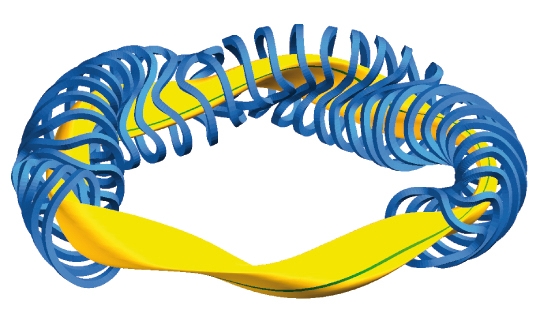
Dieses Möbiusband ist ein gutes Beispiel dafür, daß komplexe Funktionen in der Realität oft ganz einfach zu begreifen sind, weswegen sie in einigen technischen Bereichen zum Einsatz kommen. So wird zum Beispiel beim Stellarator das Plasma durch entsprechend geformte Feldspulen auf eine Möbiusband-förmige Bahn gebracht (Abbildung 5), und auch z. B. bei Riemengetrieben wird die Form des Möbiusbandes benutzt, da es für gleichmäßige Abnutzung sorgt.

Einsteins Hausaufgaben

Können wir uns jetzt nach der Messung von Gravitationswellen beruhigt zurücklehnen und sagen: „Ah, jetzt haben wir Einstein endlich begriffen!”? Vielleicht sollte man lieber sagen: Einstein zeigt uns Keplers Weg, die physikalische Realität vorurteilslos zu betrachten, d. h. wir müssen von ihm lernen, Annahmen immer wieder zu prüfen und zu hinterfragen. Dafür sind die Vorhersagen aus seiner Gravitationstheorie bedeutsam:

„Die so aus dem allgemeinen Relativitätspostulat abgeleitete Gravitationstheorie zeichnet sich nicht nur durch ihre Schönheit aus, sie beseitigt nicht nur den in § 21 beleuchteten Mangel, welcher der klassischen Mechanik anhaftet, sie interpretiert nicht nur das Erfahrungsgesetz von der Gleichheit der trägen und schweren Masse, sondern sie hat auch schon zwei wesensverschiedene Beobachtungsergebnisse der Astronomie erklärt, denen gegenüber die klassische Mechanik versagt. Das zweite dieser Ergebnisse, nämlich die Krümmung der Lichtstrahlen durch das Gravitationsfeld der Sonne, haben wir schon erwähnt; das erste betrifft die Bahn des Planeten Merkur.”¹¹

Benjamin Knispel vom Albert-Einstein-Institut für Gravitationsphysik in Hannover beschreibt Einsteins Erklärung des Paradoxes der Merkurbahn:

„Die Merkurbahn ist eine Ellipse. Normalerweise, wenn ich jetzt annehme, die Gravitation wäre so einfach wie bei Newton, wie man es in der Schule lernt, sollte diese Ellipse raumfest stehen. Das tut sie aber nicht: Sie dreht sich ein bißchen. Das liegt zum einen daran, daß die anderen Planeten mit ihrer Schwerkraft da herum ziehen. Aber wenn ich das alles weg rechne, dann bleibt immer noch so ein kleiner Rest, ganz wenig, 43 Bogensekunden pro Jahrhundert, aber man konnte das messen, auch schon Ende des 19. Jahrhunderts, und hatte keine Ahnung woran es liegt.”¹⁹

Wenn wir an Keplers Beschäftigung mit den Kegelschnitten denken und die Bedeutung, die er in ihrer Erforschung sah, begreifen wir, daß es für die Erklärung der Planetenbahnen nur eine Lösung in Einsteins vierdimensionaler Raum-Zeit geben kann. Bei genauerer Messung erkennt man, daß die Newtonsche Theorie rein willkürliche Annahmen macht, und Einstein stellt uns heute die Aufgabe, genauso wie die Merkurbahn auch die anderen Planetenbahnen genau zu prüfen:

„Spezialisiert man nämlich die Gleichungen der allgemeinen Relativitätstheorie auf den Fall, daß die Gravitationsfelder als schwach anzusehen sind, und daß alle Massen sich mit Geschwindigkeiten gegen das Koordinatensystem bewegen, welche gegen die Lichtgeschwindigkeit klein sind, so erhält man zunächst die Newtonsche Theorie als erste Näherung; letztere ergibt sich also hier ohne besondere Annahme, während Newton die dem Quadrat der Distanz aufeinander wirkender Massenpunkte indirekt proportionale Anziehungskraft als Hypothese einführen mußte.

Vergrößert man die Genauigkeit der Rechnung, so treten Abweichungen von der Newtonschen Theorie auf, die sich allerdings wegen ihrer Kleinheit fast alle noch der Beobachtung entziehen müssen. Eine dieser Abweichungen müssen wir hier speziell ins Auge fassen. Nach der Newtonschen Theorie bewegt sich ein Planet um die Sonne in einer Ellipse, welche gegenüber den Fixsternen ihre Lage ewig beibehalten würde, wenn von der Einwirkung der anderen Planeten auf den betrachteten Planeten und von der Eigenbewegung der Fixsterne abgesehen werden könnte. Korrigiert man daher die beobachtete Bewegung der Planeten auf diese beiden Einflüsse, so soll als Bahn des Planeten eine gegen die Fixsterne feste Ellipse resultieren, wenn Newtons Theorie genau richtig ist. Bei allen Planeten, bis auf den der Sonne nächsten Planeten Merkur, hat sich diese mit eminenter Genauigkeit prüfbare Konsequenz mit der Genauigkeit bestätigt, welche die heute erreichbare Beobachtungsschärfe zu erzielen gestattet. Vom Planeten Merkur aber wissen wir seit Leverrier, daß die Ellipse seiner im obigen Sinne korrigierten Bahn gegenüber den Fixsternen nicht feststeht, sondern, wenn auch ungeheuer langsam, in der Ebene der Bahn im Sinne der Umlaufbewegung rotiert.

Für diese Rotationsbewegung der Bahnellipse ergab sich ein Betrag von 43 Bogen-Sekunden pro Jahrhundert, welcher Betrag bis auf wenige Bogen-Sekunden sichergestellt ist. Die Erklärung dieser Erscheinung nach der klassischen Mechanik gelingt nur unter Zugrundelegung von ausschließlich ihrethalben ersonnenen, wenig wahrscheinlichen Hypothesen.

Nach der allgemeinen Relativitätstheorie ergibt sich, daß jede Planetenellipse um die Sonne in der oben angegebenen Weise notwendig rotieren muß, daß diese Rotation bei allen Planeten außer Merkur zu klein ist, um bei der heute erzielbaren Beobachtungsgenauigkeit festgestellt zu werden, daß sie aber bei Merkur 43 Bogen-Sekunden pro Jahrhundert betragen muß, genau wie es die Beobachtung ergeben hatte.”²⁰

Die Messung der Perihelbewegungen der Planeten stellt der heutigen Forschung eine weitere Aufgabe. Meist sind es nämlich genau diese winzigen Ungenauigkeiten, die neue Paradoxe aufzeigen und uns so dem Verständnis des Universums näherbringen. Der Kosmologe Michael Turner, Universität von Chicago, beschrieb staunend, wie Einstein uns mit diesem Suchen nach Paradoxen eine ganz neue Denkwelt eröffnet hat:

„Die Theorie, die die Bewegung Merkurs erklärt, war nicht einfach Newton und etwas mehr. Es war etwas völlig Neues: die Einsteinsche Relativitätstheorie! Diese Lehre der Wissenschaftsgeschichte sollten wir immer im Kopf haben, wenn wir uns heute mit großen Theorien über Dunkle Materie oder den Urknall beschäftigen.

Auch wenn diese nur bei kleinen, vermeintlich unwichtigen Aspekten nicht stimmig sind, so könnte das stets ein Menetekel sein. Vielleicht erwartet uns bald wieder eine viel größere Revolution, als wir uns heute vorstellen.”²¹

Deshalb ist die erfolgreiche Messung der Gravitationswellen für uns alle ein Startschuß auf dem Weg zu einer neuen Welt. Unzählige Probleme und Aufgaben liegen vor uns! Einstein hat nicht sein Leben lang gegen Newton gewettert, sondern einen neuen, besseren Weg gezeigt. Jetzt ist die Zeit, sich mit den Lösungen zu befassen. Beteiligen wir uns alle an diesem spannenden Paradigmenwandel!

1. Einsteins ehemaliger Mathematikprofessor in Zürich, Hermann Minkowski, bei der Vorstellung der Relativitätstheorie vor der Deutschen Mathematiker-Vereinigung. Veröffentlicht unter dem Titel Raum und Zeit in: Jahresberichte der Deutschen Mathematiker-Vereinigung, Leipzig, 1908 (veröffentlicht 1909).[↩]
2. Albert Einstein, Mein Weltbild, herausgegeben von Carl Seelig, Ullstein-Taschenbücher-Verlag, Frankfurt/Main, 1959, S. 146 f.[↩]
3. Einstein, Über die spezielle und allgemeine Relativitätstheorie (gemeinverständlich), Vierte Auflage, Friedrich Vieweg & Sohn, Braunschweig 1919. Alle Beiträge Einsteins in den Annalen der Physik sind im Internet zugänglich unter http://www.physik.uni-augsburg.de/annalen/history/Einstein-in-AdP.htm.[↩]
4. Ebenda[↩][↩]
5. Ilse Rosenthal-Schneider, „Begegnungen mit Einstein, von Laue und Planck – Realität und wissenschaftliche Wahrheit”, Friedrich Vieweg & Sohn, Braunschweig 1988, übersetzt aus dem amerikanischen, Reality and Scientific Truth, Wayne State University Press, Detroit/Michigan 1981.[↩]
6. Herbert Meschkowski, Von Humboldt bis Einstein. Berlin als Weltzentrum der exakten Wissenschaften, 1989, S. 240.[↩]
7. Einstein, Über die Spezielle und Allgemeine Relativitätstheorie (gemeinverständlich), a. a. O., Seite 52.[↩]
8. Herbert Meschkowski, a. a. O.[↩]
9. Fischer/Duerbeck, Hubble – Ein neues Fenster zum All, Geleitwort von Robert Williams, Birkhäuser Verlag 1995.[↩]
10. Welt der Physik, 11.2.2016, Artikel von Nora Kusche (http://www.weltderphysik.de/gebiet/astro/gravitationswellen/detektoren-undmessungen/ ) und Süddeutsche Zeitung, 11.2.2016, Interview mit Prof. Karsten Danzmann (http://www.sueddeutsche.de/wissen/physik-gravitationswellen-entdeckt-und-jetzt-1.2859488).[↩]
11. Einstein, Über die Spezielle und Allgemeine Relativitätstheorie (gemeinverständlich), a. a. O.[↩][↩][↩]
12. Einsteins Autobiographie, in: Paul Arthur Schilpp, Albert Einstein als Philosoph und Naturforscher, Kohlhammer-Verlag, Stuttgart 1955.[↩]
13. Bernhard Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen, siehe http://www.maths.tcd.ie/pub/HistMath/People/ Riemann/Geom/Geom.html[↩]
14. Nikolaus von Kues, De Quadratura Circuli.[↩]
15. Herbert Meschkowski, a. a. O., S. 41/42.[↩]
16. Einstein, Über die Spezielle und Allgemeine Relativitätstheorie (gemeinverständlich), a. a. O., S. 44.[↩]
17. Gauß, Die vier Gauß´schen Beweise für die Zerlegung ganzer algebraischer Funktionen in reelle Factoren ersten oder zweiten Grades, S. 74.[↩]
18. Siehe Caroline Hartmann, „Carl Friedrich Gauß und die Geometria Situs des Universums”, Ibykus, Nr. 58 (1/1997).[↩]
19. Dirk Lorenzen, „Einstein auf dem Prüfstand; Die Periheldrehung des Merkur”, Deutschlandfunk, 9.6.2015.[↩]
20. Einstein, Über die Spezielle und Allgemeine Relativitätstheorie (gemeinverständlich), Zweiter Teil: „Über die allgemeine Relativitätstheorie”, Seite 69 ff.[↩]
21. Dirk Lorenzen, „Einstein auf dem Prüfstand; Die Periheldrehung des Merkur”, a. a. O.[↩]