Nicht-Newtonische Mathematik für Ökonomen

Dieser Artikel von Lyndon LaRouche erschien ursprünglich auf englisch in Executive Intelligence Review, Vol. 22, Nr. 32, vom 11. August 1995 als Fortsetzung seines Artikels „Why Most Nobel Prize Economists Are Quacks“ (Executive Intelligence Review, Vol. 22, Nr. 30, 28. Juli 1995), worin LaRouche seine Überlegungen zu Fragen der mathematischen Darstellung der für realwirtschaftliche Prozesse charakteristischen Ursache-Wirkungs-Beziehungen darstellte. In der vorliegenden Arbeit schildert er die Methode, die dabei zur Anwendung kommen muß.

---

Der voranschreitende Zusammenbruchsprozeß des vom Internationalen Währungsfonds dominierten globalen Währungs- und Finanzsystems verdeutlicht unter anderem, daß alle allgemein akzeptierten mathematischen Darstellungen von Wirtschaftsprozessen verheerend inkompetent sind. Die kompetente Alternative dazu wird als LaRouche-Riemann-Methode bezeichnet. Allerdings sollte von einer Welt, die so sehr unter der Politik amerikanischer Nobelpreisträger gelitten hat, nicht verlangt werden, eine alternative Wirtschaftslehre in blindem Vertrauen zu akzeptieren. Deshalb reicht es nicht aus, zu wissen, daß die LaRouche-Riemann-Methode funktioniert; es ist notwendig, nachvollziehbar zu machen, wie und warum sie funktioniert.

Bei der Auswahl einer Meßmethode zur Darstellung realer ökonomischer Prozesse müssen zwei Probleme behandelt werden. Die Hauptaufgabe besteht darin, eine Methode zur Darstellung des realwirtschaftlichen Prozesses als solchem zu definieren: Dieser Prozeß ist charakteristisch „nicht-entropisch“.((Zur Verwendung des Begriffs „Nicht-Entropie“ durch den Autor: Seit mehr als einem Jahrhundert ist es eine weithin akzeptierte Lehrmeinung, daß alle anorganischen Prozesse dazu neigen, abzulaufen; diese Aussage wurde von Lord Kelvin in der Mitte des letzten Jahrhunderts gemacht. Auf Kelvins Geheiß wurde seine Lehre von zwei deutschen Wissenschaftlern, Rudolf Clausius und Hermann Grassmann, in eine mathematische Form gebracht, wobei sie ihr eigenes kinematisches Modell des Wärmeaustauschs in einem imaginären, abgeschlossenen, besonderen Gassystem verwendeten, um so angeblich die kalorische Wärmetheorie des französischen Wissenschaftlers Sadi Carnot zu erklären. Kelvin und seine Kollegen definierten den „Reibungsverlust“ in einem solchen mechanischen Modell eines thermodynamischen Systems als „Entropie“. Dies war Kelvins zweiter Hauptsatz der Thermodynamik. In den 1940er Jahren verwendete Prof. Norbert Wiener vom Massachusetts Institute of Technology den Begriff „negative Entropie“ (verkürzt auf den Neologismus „Negentropie“), um die statistische Form „umgekehrter Entropie“ im Sinne einer berühmten Rekonstruktion des Clausius-Grassmann-Modells durch Ludwig Boltzmann zu bezeichnen: Boltzmanns sogenanntes H-Theorem. Wieners Argument diente dann dazu, das später als „Informationstheorie“ bekannt gewordene Konzept zu begründen. In diesem Zusammenhang behauptete Wiener, daß das H-Theorem ein statistisches Mittel zur Messung des „Informationsgehalts“ nicht nur von verschlüsselten elektronischen Übertragungen, sondern auch von der Ideen-Kommunikation des Menschen darstelle. Zuvor diente der Begriff „negative Entropie“ als Merkmal der offenbaren Verletzung von Kelvins sogenanntem „Zweiten Hauptsatz“ durch lebende Prozesse im allgemeinen – im Unterschied zu den scheinbar entropischen Merkmalen gewöhnlicher nicht-lebender Phänomene. Mehrere Jahrzehnte lang, beginnend 1948, bestand der Verfasser darauf, daß nur die erste Bedeutung von „Negentropie“ im Sinne der allgemein charakteristischen Unterscheidung lebender Prozesse zum Gebrauch akzeptiert werden sollte. Vor kurzem hat er dafür aus praktischen Gründen den Begriff „Nicht-Entropie“ verwendet.)) Die zweite, aber genauso entscheidende Aufgabe besteht darin, die Wechselwirkung zwischen diesem wirtschaftlichen Prozeß und dem überlagerten, charakteristisch linearen (und daher entropischen) Geld- und Finanzsystem darzustellen.

Die zur Darstellung der Realwirtschaft erforderliche Methode, der physikalisch-ökonomische Prozeß, wird im folgenden Schritt für Schritt beschrieben.

LaRouches Entdeckung

Die Entdeckung, auf der die LaRouche-Riemann-Methode beruht, wurde ursprünglich im Zeitraum 1948–52 entwickelt. Sie entstand in Hinblick auf einen engeren Zweck, nämlich die Absurdität der Behauptung von Prof. Norbert Wiener aufzuzeigen, daß die Kommunikation menschlicher Konzepte mit Hilfe seiner statistischen „Informationstheorie“((Norbert Wiener, Cybernetics (John Wiley, New York, 1948). Schon vor 1948 hatte sich der Autor zwei wesentliche Voraussetzungen angeeignet, um Wieners Thesen kompetent angreifen zu können. Bereits Ende der 1930er Jahre hatte der Autor als überzeugter Anhänger von Gottfried Wilhelm Leibniz intensiv daran gearbeitet, einen Beweis für die Absurdität der gegen Leibniz gerichteten Argumente aufzustellen, die in Immanuel Kants Kritik der reinen Vernunft eine zentrale Bedeutung einnahmen. 1948 erkannte er in den entscheidenden Trugschlüssen von Wieners „statistischer Informationstheorie“ eine grobe Kopie des zentralen wissenstheoretischen Arguments in Kants drei berühmten Kritiken. Zweitens hatte der Autor 1946–47 eine eigene, etwas kritische Sicht über die Verwendung des Begriffs „negative Entropie“ in der Biologie, wie z. B. bei Lecomte du Nouÿ, entwickelt.)) gemessen werden könne. Die Entscheidung, realwirtschaftliche Fakten für die Widerlegung Wieners zu verwenden, führte zu der Entdeckung.

Das ursprüngliche Argument gegen Wieners Behauptung lautete, daß sich die menschliche „Ökologie“ von der Ökologie niederer Arten generell genauso unterscheidet, wie sich lebende Prozesse herkömmlich von sogenannten nichtlebenden Prozessen unterscheiden. Diese Auffassung ging von der Tatsache aus, daß die Erhöhung der potentiellen relativen Bevölkerungsdichte((Lyndon H. LaRouche jr., Was Sie schon immer über Wirtschaft wissen wollten, Böttiger-Verlag, Wiesbaden, 1985, passim. „Relativ“ in „potentielle relative Bevölkerungsdichte“ bedeutet schlicht und einfach die Qualitätsunterschiede in den unterschiedlichen vom Menschen entwickelten und vom Menschen erschöpften Lebensumfeldern.)) der menschlichen Gattung, etwa durch technischen Fortschritt, eine Folge klar unterscheidbarer Phasensprünge darstellt: daß diese charakteristischen Phasensprünge in der gesellschaftlichen Entwicklung die menschliche Gattung absolut von allen niederen Gattungen unterscheiden.

Die anfängliche Darstellung dieser Unterscheidung zwischen dem Menschen und untergeordneten Gattungen war vom Standpunkt der Geometrie elementar. Jede logisch konsistente mathematische Darstellung eines bestehenden Spektrums von Technologien läßt sich in realer Annäherung als ein deduktives Theoremgitter beschreiben. Jede gültige Entdeckung eines höheren Prinzips wirkt sich auf die mathematische Physik aus, indem sie zum Beispiel eine entsprechende Änderung in den formalen und ontologischen Axiomen erfordert, die der bisherigen, allgemein akzeptierten Form der mathematischen Physik zugrunde liegen. Es ist die kumulative Abfolge solcher effizient fortschreitender, axiomatischer Veränderungen des menschlichen Wissens für die Praxis, die der Abfolge von Phasensprüngen im Bereich der potentiellen relativen Bevölkerungsdichte der Gesellschaft entspricht.

Diese Sichtweise definierte ein implizites, funktionales Ordnungsprinzip, das der Erhöhung der potentiellen relativen Bevölkerungsdichte zugrunde liegt. Die ursprüngliche These aus der Zeit von 1948–54 lautete zusammenfassend wie folgt. Man betrachte den physischen und verwandten Konsum durch die Haushalte und den Produktionszyklus als analog zur Verwendung des Begriffs „Systemenergie“ in der gewöhnlichen Thermodynamik. Gesellschaften steigen oder fallen in dem Maße, wie sie nicht nur den Bedarf an „Systemenergie“ decken, sondern auch eine bestimmte höhere Outputmenge jener Qualitätsanforderungen erzeugen, die der „freien Energie“ entsprechen. Daraus ergibt sich implizit ein Verhältnis von „freier Energie“ zu „Systemenergie“.

Eine zusätzliche Überlegung ist entscheidend. Soll sich die Gesellschaft entwickeln, muß ein bedeutender Teil dieser „freien Energie“ in Form von „Systemenergie“ „reinvestiert“ werden. Dadurch soll nicht nur der Umfang der Gesellschaft erweitert werden; auch die relative „Kapitalintensität“ und „Energieintensität“ der gesellschaftlichen Produktion pro Kopf und pro Flächeneinheit müssen sich erhöhen. Deswegen muß ein gewisser Mindestwert des Verhältnisses zwischen „freier Energie“ und „Systemenergie“ aufrechterhalten werden, trotz steigender „Kapitalintensität“ und „Energieintensität“ des für den Produktionszyklus verwendeten Modus. Diese Randbedingung (oder Reihe von Ungleichheiten) diente dazu, um die korrekte Verwendung des Begriffs „Negentropie“ als Gegenposition zu Wieners Verwendung des Begriffs zu definieren. Seit kurzem verwende ich den Begriff „Nicht-Entropie“, da er diesem Zweck besser dient (siehe die Darstellung über die Maßverhältnisse in der Realwirtschaft am Ende dieses Artikels).

Um 1949–50 nahm das Argument gegen Wiener diese Form an. Denn das charakteristische Unterscheidungsmerkmal der menschlichen Gattung ist die Reihe von Phasensprüngen in der potentiellen relativen Bevölkerungsdichte, die so beschreibbar sind: Die Ideen, die für das erfolgreiche Denken der Kulturen charakteristisch sind, sind Ideen, die effizient solche Veränderungen in der Praxis bewirken, die tendenziell die potentielle relative Bevölkerungsdichte der menschlichen Gattung erhöhen. Der implizite soziale Inhalt jeder gültigen axiomatisch-revolutionären Entdeckung in Wissenschaft oder Kunst definiert das menschliche Wissen: nicht Wieners mechanistische Statistikmethode.

Es war bereits zu diesem Zeitpunkt der Untersuchung offensichtlich, daß keine herkömmliche Lehrbuchmathematik geeignet war, diese Art von „nicht-entropischem“ Wirtschaftsprozeß abzubilden. Die zentrale Funktion gültiger axiomatisch-revolutionärer Ideen lokalisiert die Funktion des Wirtschaftswachstums in den revolutionären Veränderungen der Axiome als solchen. Das so dargestellte mathematische Problem besteht darin, daß Veränderungen in den Axiomenreihen, die den deduktiven Theoremgittern zugrunde liegen, die Form absoluter mathematischer Unstetigkeiten haben. Das heißt: Es gibt keine formale Methode, um das neue Gitter deduktiv aus dem alten Gitter abzuleiten. Eine solche mathematische Unstetigkeit hat eine Größenordnung von unbegrenzter Kleinheit, die niemals den tatsächlichen Nullpunkt erreicht. Das impliziert die Existenz sehr wirkungsvoller, extrem nützlicher mathematischer Funktionen, aber keine gewöhnliche Mathematik kann mit Funktionen umgehen, die in Form solcher Unstetigkeiten ausgedrückt sind. Um die ursprüngliche Entdeckung des Autors anwenden zu können, mußte dieses Problem der mathematischen Darstellung als nächstes angegangen werden. Eine mathematische Lösung wäre wünschenswert, aber ein konzeptioneller Überblick war unerläßlich.

Der nächste Schritt war somit Anfang 1952 eine Untersuchung von Georg Cantors Studien über diese Art von mathematischen Unstetigkeiten.((Georg Cantor, „Beiträge zur Begründung der transfiniten Mengenlehre“, Georg Cantors Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, hrsg. von Ernst Zermelo, 1932, Verlag Julius Springer, Berlin, 1990, S. 282–356 [im folgenden „Abhandlungen“].)) Cantors Arbeiten über das mathematisch Transfinite, insbesondere seiner sogenannten Aleph-Reihe, wiesen den Weg zu einer tieferen Würdigung der Habilitationsschrift von Bernhard Riemann aus dem Jahr 1854. Umgekehrt zeigte Riemanns fundamentale Entdeckung von der Verallgemeinerung „nicht-euklidischer“ Geometrien, wie wir uns Cantors funktionalen Begriff der implizit abzählbaren Dichte mathematischer Unstetigkeiten pro willkürlich gewähltem Wirkintervall vorstellen müssen.

Dieser Begriff der relativen Dichte von Unstetigkeiten ist die richtige Beschreibung der Kultur, die die Gesellschaft ihren Jugendlichen vermitteln sollte.((Oder, man könnte sagen, relative Kardinalität oder Mächtigkeit.)) Der Begriff „Dichte“ bezieht sich auf die Menge jener gültigen wissenschaftlichen und künstlerischen Entdeckungen (z. B. gültige axiomatisch-revolutionäre Veränderungen), die die Menschheit bis heute angesammelt hat, um sie auf die Bildungserfahrung junger Menschen zu übertragen.

Sobald man erkennt, daß Cantor in seinem Werk die frühere Entdeckung Riemanns wieder aufnimmt, ist es von offensichtlichem Vorteil, Riemanns geometrischen Ansatz gegenüber dem relativ formalistischen Weg, den Cantor beschreitet, zu wählen.((Infolge der Kontrolle der Berliner Akademie der Wissenschaften durch den Newton-Verehrer Friedrich II. von Preußen und der anschließenden Übernahme der französischen École Polytechnique durch die Newtonianer Laplace und Cauchy nach 1814 wurde die geometrische Methode von Platon, Cusa, Leonardo da Vinci, Kepler und Leibniz immer mehr durch die Methode der unendlichen algebraischen Reihen verdrängt. Am bedeutsamsten dabei war Leonhard Eulers Angriff auf Leibniz in der Frage der unendlichen algebraischen Reihen: Euler leugnete die Existenz absoluter mathematischer Unstetigkeiten. Der politische Erfolg der Newtonianer, die im Laufe des 19. Jahrhunderts Eulers unendliche Reihen für natürliche Logarithmen als Standard für mathematische Beweise etablierten, führte zum Positivismus von Russell-Whitehead in der Principia Mathematica und dem damit verbundenen wilden Extremismus der heutigen „Chaostheorie“. So griffen Karl Weierstraß und sein früherer Schüler Georg Cantor zwar dasselbe allgemeine Problem der Mathematik an wie Riemann, nämlich die Existenz von Unstetigkeiten, und engagierten den Newtonschen Gegner auf seinem eigenen Terrain, den unendlichen Reihen, während Riemann das Problem vom Standpunkt der Geometrie aus angriff: daher Riemanns deutlich größerer Erfolg für die Physik.)) Bei produktiven und verwandten Prozessen in der modernen Wirtschaft sind die Konzepte, die dem Entwurf wissenschaftlicher Experimente und abgeleiteter Werkzeugmaschinenkonzepte zugrunde liegen, von Natur aus geometrischer Natur. Wenn man über Produktion und Wirtschaft nachdenkt, muß man geometrisch und nicht algebraisch denken.

Daher hat der Verfasser, der mit Hilfe von Riemanns Werk die mathematischen Implikationen seiner eigenen früheren Entdeckung in der Ökonomie behandelte, die scheinbar anomale, aber sehr treffende Bezeichnung „LaRouche-Riemann-Methode“((Der Verfasser hatte zwar bereits in seinem einsemestrigen Kurses, den er in den Jahren 1966–73 an verschiedenen amerikanischen Universitäten abgehalten hat, beständig seinen Dank gegenüber Riemann ausgedrückt, doch erstmals öffentlich wurde der Begriff „LaRouche-Riemann-Methode“ im November 1978 im Rahmen eines gemeinsamen Wirtschaftsprognose-Projekts von Executive Intelligence Review und der Fusion Energy Foundation verwendet. Auslöser dafür war damals die Überlegung, daß die isentropische Kompression bei der Kernfusion, wie sie 1859 in Riemanns Aufsatz „Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite“ mathematisch vordefiniert wurde, mathematische Analogien zur Ausbreitung „Stoßwellen“-ähnlicher Phasensprünge hat, die durch technologische Revolutionen erzeugt werden. (Siehe Riemann, Werke, zitiert in Fußnote 8 unten, S. 145 ff.) Als Nebenprodukt dieses gleichen, sehr erfolgreichen Prognoseprojekts wurde von derselben Arbeitsgruppe eine englische Übersetzung des Riemann-Papiers angefertigt; sie erschien in The International Journal of Fusion Energy, Band 2, Nr. 3, 1980, S. 1–23, unter dem Titel „On the Propagation of Plane Airwaves of Finite Amplitude“. Die Betonung von Riemanns „Stoßwellen“-Artikel spiegelte einen damaligen freundschaftlichen Streit zwischen der Organisation des Autors und den Lawrence Livermore Laboratories über die Mathematik der thermonuklearen Zündung beim Trägheitseinschluß wider. Bemerkenswert ist, daß bei diesem Konflikt der Einfluß von Theodore von Karman, eines anglophilen Wissenschaftsberaters des U.S. Army Air Corps, eine Rolle spielte, der Lord Rayleighs inkompetenten Fanatismus gegen Riemanns Methode unterstützte. Zum Erfolg der vierteljährlichen EIR-Wirtschaftsprognosen von 1979–83 siehe David P. Goldman, „Volcker Caught in Mammoth Fraud“, Executive Intelligence Review, Bd. 10, Nr. 42, 1. November 1983.)) gewählt. Untersuchen wir die elementarsten Aspekte von Riemanns Habilitationsschrift.((Bernhard Riemann, „Über die Hypothesen, welche der Geometrie zu Grunde liegen“, Gesammelte mathematische Werke und wissenschaftlicher Nachlass [im folgenden als Riemanns Werke bezeichnet], hrsg. von Heinrich Weber, S. 254 ff. Wer sich mit den formal-mathematischen Implikationen der Dissertation als solcher beschäftigen will, wird auf die spätere (1858) Pariser Darstellung verwiesen: „Commentatio mathematica, qua respondere tentatur quaestioni ab Illma Academia Parisiensi propositae“, Werke, S. 370–383 (lateinisch), mit angehängten Anmerkungen von Weber, S. 384–399 (deutsch).)) Der Klarheit halber wiederholen wir in den folgenden Passagen mehrere der oben genannten Punkte.

Am Ende seiner berühmten Habilitationsschrift von 1854 „Über die Hypothesen, welche der Geometrie zu Grunde liegen“ faßt Riemann seine Argumentation zusammen: „Es führt dies hinüber in das Gebiet einer andern Wissenschaft, in das Gebiet der Physik, welches wohl die Natur der heutigen Veranlassung [d. h. der Mathematik – LHL] nicht zu betreten erlaubt.“((Bernhard Riemann, ebenda, S. 268.)) In der heutigen Wissenschaftssprache hat diese Aussage Riemanns die folgende wichtige Bedeutung für die Konstruktion einer mathematischen Konzeption, die in der Lage ist, realwirtschaftliche Prozesse adäquat darzustellen.

Jedes deduktive mathematische System kann als ein formales Theoremgitter beschrieben werden. Ein Theorem in einem solchen Gitter ist jede Aussage, die nachweislich nicht im Widerspruch zu einer zugrundeliegenden Reihe miteinander verbundener Axiome und Postulate steht.((Platons Begriff für die Reihe von Axiomen und Postulaten, die einem Theoremgitter zugrunde liegen, ist Hypothese.)) Das maßgebliche Bezugsmodell für ein solches Theoremgitter ist entweder eine Euklidische Geometrie oder, vorzugsweise, jene konstruktive Geometrie, die mit berühmten Namen wie Gaspard Monge, Adrien M. Legendre und Bernhard Riemanns Geometrielehrer Jacob Steiner verbunden ist.

Daraus ergibt sich die Schwierigkeit, daß jede Änderung innerhalb dieser Reihe von Axiomen und Postulaten ein neues Theoremgitter erzeugt, das mit dem ersten durchgehend inkonsistent ist. Diese Inkonsistenz zwischen beiden drückt sich anderweitig als mathematische Unstetigkeit oder Singularität aus. Wenn man die Existenz einer solchen Unstetigkeit auf diese Weise definiert, bedeutet das, daß kein Theorem des zweiten Theoremgitters direkt vom Ausgangspunkt des ersten zugänglich ist, es sei denn, man führt in die Axiomenreihe eine Operation ein, die für die relevante Änderung verantwortlich ist.

Mit anderen Worten, man muß die bereits vorhandene Mathematik verlassen und einen Umweg über die Physik als solche nehmen, um zum zweiten der beiden mathematischen Theoremgitter zu gelangen. Die entscheidende Bezugsgröße, die wir an dieser Stelle einführen müssen, wie sie von Nikolaus von Kues in seinem Werk, das die moderne Wissenschaft begründete,((Nikolaus von Kues, De Docta Ignorantia, 1440, (deutsch Über die belehrte Unwissenheit), Meiner-Verlag, 1994, passim.)) genauso wie auch von Riemann festlegt wurde, ist „Messung“.((Bernhard Riemann, „II. Maßverhaeltnisse, deren eine Mannigfaltigkeit von n Dimensionen fähig ist …“, in Werke, a. a. O., S. 258 ff.)) Betrachten wir die vom Verfasser bevorzugte und häufig verwendete Illustration des betreffenden Prinzips: Die von Eratosthenes, dem berühmten Mitglied von Platons Athener Akademie, berechnete Größe des durch die Erdpole verlaufenden Längenkreises – eine Messung der Erdkrümmung während des 3. Jahrhunderts v. Chr., 22 Jahrhunderte bevor irgendein Mensch die Erdkrümmung überhaupt gesehen hat.((Siehe Greek Mathematical Works, Bd. II, trans. by Ivor Thomas (Harvard University Press, Loeb Classical Library, Cambridge, Massachussets, 1980), S. 266–273. Vgl., Lyndon H. LaRouche jr., „What is God, That Man Is In His Image“, Fidelio, Vol. IV, No. 1, Spring 1995, S. 28–29.)) Eine doppelte Feststellung soll hier kurz angesprochen werden.

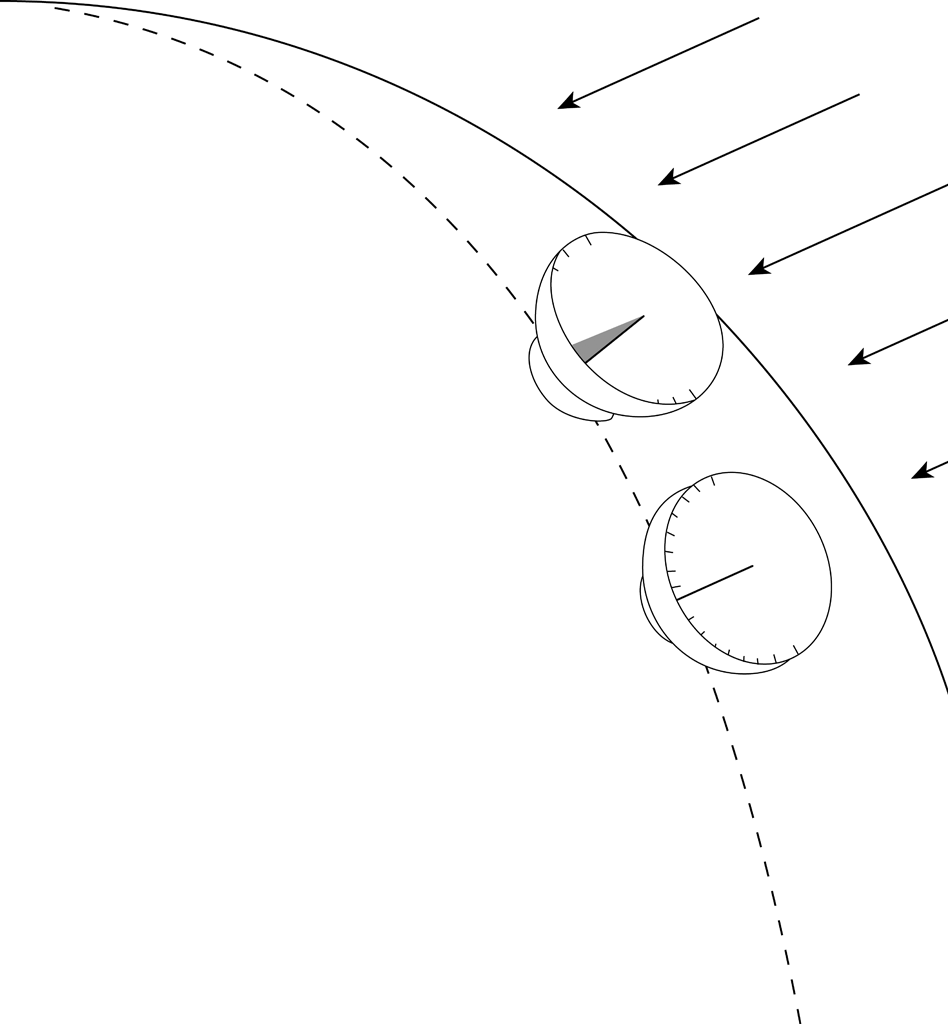
Um mit Hilfe der Astronomie eine Nord-Süd-Linie (einen Längenkreis) zu bestimmen, wählt man zwei Punkte von beträchtlicher, aber meßbarer Entfernung auf dieser Linie. Diese Entfernung wird gemessen. An jedem der beiden Punkte werden identische Sonnenuhren aufgestellt. Man mißt den Schatten, den ein vertikaler Stab zur Mittagszeit desselben Tages wirft, und vergleicht die Winkel der jeweiligen Schatten. Der Unterschied zwischen beiden Winkeln läßt darauf schließen, daß die Erde nicht flach ist, sondern eine bestimmte Krümmung hat (siehe Abbildung 1). Mit Hilfe des geometrischen Prinzips von Ähnlichkeit und Proportion berechnet man auf Grundlage der gemessenen Länge des Bogenabstands zwischen den beiden Punkten die Größe des durch die beiden Pole der Erde verlaufenden Kreises. Eratosthenes irrte sich bei seiner Berechnung des Poldurchmessers der Erde um etwa 85 Kilometer.((ebenda))

Zwei Aspekte werden an diesem Beispiel deutlich.

Zunächst veranschaulicht dieses Beispiel, was Platon unter einer Idee versteht. Da diese Messung vor 22 Jahrhunderten stattfand, als noch niemand die Erdkrümmung gesehen hatte, war das, was gemessen wurde, kein durch Sinneswahrnehmung definiertes Objekt. Natürlich bediente man sich der Sinne; aber die Idee der Erdkrümmung entstand aus dem Wissen, daß sich die Eindrücke der Sinne selbst widersprechen: Die unterschiedlichen Winkel des Schattens an den beiden Orten war der empirische Ausdruck dieser sich selbst widersprechenden Qualität. Man mußte somit Vorstellungen entwickeln, die außerhalb des Bereichs der Sinneswahrnehmungen lagen – in dem Bereich, den Platon als Ideen definiert.((Unterteilen wir den Bereich der Wissenschaft als Ganzes in drei thematische Bereiche, die sich durch die Grenzen der menschlichen Sinneswahrnehmungsfähigkeit voneinander unterscheiden. Das, was durch den Sinnesapparat als Phänomen erkannt werden kann, nennen wir die Domäne der Makrophysik. Was im sehr Großen nicht zugänglich ist (wie etwa das Phänomen, die Entfernung zwischen Erde und Mond direkt zu sehen), gehört zur Domäne der Astrophysik. Phänomene, die in einem zu kleinen Maßstab auftreten, um direkt von unseren Sinnen unterschieden werden zu können, befinden sich in der Domäne der Mikrophysik. Somit gehören die grundlegendsten physikalischen Ideen der Astro- und Mikrophysik vollständig in den Bereich platonischer Ideen. Rigorose Bemühungen des Schülers, die Entdeckungen von Platons Athener Akademie und von Archimedes aus dem 4. und 3. Jahrhundert v. Chr. nachzuvollziehen, sind die Voraussetzung dafür, sein Urteilsvermögens auszubilden, um sich mit Fragen der Astrophysik und Mikrophysik beschäftigen zu können. Von noch grundlegenderer Bedeutung ist das, was man im Unterricht als vierte Abteilung wissenschaftlicher Ereignisse zurückhalten könnte: Kausalität. Die Sinne könnten uns niemals die Ursache selbst solcher Ereignisse zeigen, die durch Sinneswahrnehmung schlüssig erkannt werden könnten: Ursächlichkeit existiert für die Erkenntnis nur im Bereich platonischer Ideen.))

Zweitens führt dies – wie auch verwandte altgriechische Entdeckungen – in die moderne Geodäsie, die von Riemanns wichtigstem Lehrer, Carl F. Gauß, entwickelt wurde: die Messung von Entfernungen auf der Erdoberfläche unter der Kontrolle entsprechender astronomischer Messungen.((Siehe Carl Friedrich Gauß, Werke, Band IX, Georg Olms Verlag, Hildesheim, New York, 1981, passim.))

Mancher Leser könnte versucht sein, einzuwenden: „Warum nicht einfach ,Trigonometrie‘ sagen? Warum den für den Laien wahrscheinlich fremden Begriff ,Geodäsie‘ verwenden?“ Der Kritiker würde damit einen schwerwiegenden Fehler begehen, eine Art Fehler, der von direkter Relevanz für die vorliegende Frage ist. Als Anleitung ausgedrückt, läßt sich die Kritik so widerlegen: Wir sollten das, was wir zu wissen behaupten, immer in Hinblick auf die Art angeben, wie wir es in Erfahrung gebracht haben. Indem wir sokratisch erkennen, daß entweder wir oder diejenigen, die uns unterwiesen haben, bei der Bildung einer Konzeption einen wichtigen Urteilsschritt übersehen oder ausgelassen haben könnten, werden entscheidende Beurteilungsfehler aufgedeckt und korrigiert. Weiter gefaßt entwickelt sich eine echte wissenschaftliche Strenge dadurch, daß man die Art und Weise, wie wir uns Vorstellungen angeeignet haben, überdenkt und diesen Prozeß als Gegenstand erkenntnistheoretischer Untersuchungen betrachtet. Laienhaft ausgedrückt: daß wir gegebenenfalls herausfinden, worüber wir überhaupt sprechen.

Wir sollten Eratosthenes‘ Entdeckungsakt in einer Weise definieren, wir wir diesen kompetent replizieren können. Es war die Astronomie, mit deren Hilfe Eratosthenes den Erdumfang berechnete. Er benutzte dabei Methoden, die mit dem früheren Beweis des Aristarchos in Zusammenhang stehen, daß die Erde die Sonne umkreist, und auch Methoden, mit denen Eratosthenes die Entfernung des Mondes von der Erde abschätzte, letztere eine Entfernung, die Menschen erst 2200 Jahre später gesehen haben. Nur das ist es, was wir in dieser Angelegenheit wissen; es sollte niemals auf andere Art und Weise ausgedrückt werden.

Verstöße gegen unsere hier dargestellte methodologische Vorschrift waren ausschlaggebend dafür, daß zum Beispiel Isaac Newton zu seiner abwegigen Behauptung et hypotheses non fingo („Ich erfinde keine Hypothesen“) gekommen ist, und daß Newton und seine Anhänger zahlreiche weitere Betrügereien verübten, die von späteren Studentengenerationen leichtgläubig übernommen wurden. Wie Riemann betonte, hatte Newton im Gegensatz zu seiner etwas hysterischen Behauptung, er mache keine Hypothesen, durchaus eine sehr offensichtliche hypothetische Annahme aufgestellt, auf der seine mathematische Physik vollständig beruht. Riemann erkannte einen Aspekt dieses Fehlers;((Riemann, Werke, S. 493.)) man kann aber mit Hilfe der gleichen Methode, die Riemann dort anwendet, zeigen, daß die Gesamtheit des Newtonschen Systems im heutigen Unterrichtssystem auf der gleichen irrtümlichen Hypothese beruht. Hätten Newton oder seine Anhänger genauer auf die Methode geachtet, mit der die Newtonianer tatsächlich zu den Auffassungen kamen, die sie als ihr Wissen ausgeben, hätten sie es wahrscheinlich nicht gewagt, weiter solche Fehler zu begehen oder ihr rituelles hypotheses non fingo zu skandieren.

Alle, die behaupten, die Antwort zu kennen, weil sie sie im hinteren Teil des Lehrbuchs nachgeschlagen haben oder weil jemand sie ihnen gesagt hat, haben diese Antwort lediglich „gelernt“, so wie ein Hund gelernt haben könnte, einen Stock zu apportieren. Diejenigen, die die Antwort nicht nur gelernt haben, sondern sie kennen, wissen sie nur, weil sie entweder die ursprüngliche Entdeckung gemacht oder sie Schritt für Schritt nacherlebt haben. Was wir wissen – Erkenntnis – ist nicht die Frucht von Sinnesgewißheit, sondern vielmehr das, was wir uns durch die rigorose Demonstration von Ideen angeeignet haben, welche nicht nur die Auslegung von Augenzeugenberichten sein konnten. Dieser Aspekt, die Frage der methodischen Transparenz, ist der offensichtlichste und entscheidendste Fehler praktisch aller allgemein anerkannter Ökonomen, die vorgeben, sich mit einem in Wirklichkeit so ontologisch komplexen Thema wie der mathematischen Sichtweise realer wirtschaftlicher Prozesse befaßt zu haben.

Für den kompetenten Ökonomen, wie für den bedachten Physiker, ist der Grundfehler aller Empirie: Ähnlich wie der traditionelle Aristoteleanismus, von dem er abgeleitet ist, behauptet der Empirismus, sich nur mit der Messung beobachteter Phänomene zu befassen, frei von der Annahme irgendeiner leitenden Hypothese. Für diesen Betrug steht Newtons et hypotheses non fingo. Im Gegensatz dazu besteht die unverzichtbare Rolle einer kontinuierlich verbesserten formalen Mathematik darin, leistungsfähigere Analyseinstrumente zu schaffen, mit denen die Konsistenz jedes beliebigen formalen Theoremgitters geprüft werden kann. Eine effektive Wissenschaft erfordert es, daß wir in der Lage sind, direkter und schneller die Eigenart von Inkonsistenzen zwischen der einem Theoremgitter zugrunde liegenden axiomatischen Basis und einer gegebenen, empirischen oder anderen Hypothese über ein mögliches Meßverfahren aufzudecken.((Solche Inkonsistenzen beweisen an sich weder, daß das Theorem noch die Mathematik falsch wären. Sie zwingen uns, die Idee der Existenz solcher Inkonsistenzen zu hinterfragen.)) Eratosthenes‘ erwähnte Messung des Meridians ist eine einfache Illustration dieses wissenschaftlichen Prinzips: das Prinzip wissenschaftlicher, d. h. platonischer Ideen.

In der Mathematik oder mathematischen Physik lassen sich solche platonischen Ideen in Form einer Axiomenreihe veranschaulichen, die jedem formalen System zugrunde liegen, als das, was Platon und Riemann als Hypothese bezeichnen. Wenn man von formalen Theoremgitter-Systemen spricht, wie z. B. einer formalen Mathematik, bedeutet „Hypothese“ die Menge der axiomatischen Annahmen, die allen beweisbaren Theoremen eines bestimmten Typs von Theoremgitter zugrunde liegen (wie z. B. einer Euklidischen Geometrie, einer linearen Algebra usw.).((Kurz gesagt, wenn jemand den Begriff „Hypothese“ als Synonym für die „vermutete“ oder „intuitive“ Lösung eines Rätsels verwendet, erweist er sich als wissenschaftlicher Analphabet. Diese Art von Analphabetismus entspricht jedoch nicht genau der Art, wie Isaac Newton denselben Begriff mißbraucht; Newtons Argument ist das eines radikalen philosophischen Empirikers in der Tradition von Sarpi, Galileo, Hobbes, Descartes und anderen. Newton behauptet, er verlasse sich ausschließlich auf Sinnesgewißheit. Newton behauptet – wenn auch zu Unrecht –, daß es in seinem System nur „natürliche Bestandteile“ von Sinnesphänomenen gebe.))

Ein Gymnasialschüler mit einer guten klassisch-humanistischen Bildung würde bereits einige Präzedenzfälle hierfür beherrschen:

1. Aus der Arbeit von Platons Athener Akademie und von Archimedes wäre er vertraut mit der Unterscheidung zwischen mathematischen Systemen, die sich auf „Kommensurable“ beschränken, und den sogenannten „Inkommensurablen“.
2. Er würde den schlüssigen Beweis von Nikolaus von Kues für die Aufteilung des Bereichs der „Inkommensurablen“ in „irrational“ und „transzendental“ kennen.
3. In seinem Einführungsunterricht in der Analysis hätte dieser Schüler auch verstanden, wie Leibniz und Jean Bernoulli die Inkompetenz der „algebraischen Methoden“ (z. B. der „unendlichen Reihen“) von Descartes und Newton aufgezeigt haben und warum aus Sicht der Physik der Lichtbrechung „algebraische“ Methoden durch „nicht-algebraische“ oder „transzendente“ Funktionsbegriffe der Mathematik ersetzt werden müssen.
4. Er könnte auch wissen, daß sich die Riemannschen Oberflächenfunktionen und Cantors Aleph-Reihe auf das Verständnis mathematischer Unstetigkeiten zurückführen lassen, die für Cusas mathematische Arbeit und für Leibniz‘ Formulierung der Differentialrechnung von zentraler Bedeutung waren, wohingegen der Newton-Anhänger Leonhard Euler diesen Unstetigkeitsbegriff hysterisch verneint hat.

Wie historisch zum Beispiel bei der Unterordnung aller Größenbegriffe unter die Verallgemeinerung der „Inkommensurablen“ erfährt die Mathematik jedes Mal eine axiomatische Veränderung innerhalb ihrer zugrundeliegenden Annahmen, ihrer Hypothese. Aufbauend auf Ole Rømers Messung der Lichtgeschwindigkeit haben Leibniz und Bernoulli so durch den Beweis für die im Experiment nachweisbare Natur der Lichtbrechung den Bereich des Transzendentalen etabliert, wie ihn schon Nikolaus von Kues gefordert hatte, der das isoperimetrische Prinzip((Nikolaus von Kues, a. a. O., passim. Cusa überarbeitete Archimedes‘ Lehrsätze über die Quadratur des Kreises, wodurch ein überlegener Ansatz für Archimedes‘ Bestimmung von π entstand. Diese Entdeckung wurde in De Docta Ignorantia (1440) aufgenommen: eine formale Ausarbeitung lieferte Cusa dann in seinem „Über die Quadratur des Kreises“ (1450). Das neue Hypothesenprinzip, das Cusa auf der Grundlage seines Nachweises der Transzendenz von π entwickelt, ist als isoperimetrisches Prinzip bekannt: Die Euklidschen Axiome, daß Punkt und Gerade selbstevident seien, werden verworfen und durch jenes isoperimetrische Prinzip ersetzt, das in erster Näherung die Kreisbewegung als primär (d. h. „selbstevident“) behandelt.)) einführte, das die axiomatische Grundlage für die Mathematik des transzendentalen Bereichs darstellt. Die lineare Hypothese der euklidischen Raumzeit (axiomatische Selbstevidenz von Punkten und Linien) wurde durch das Prinzip der Zykloide abgelöst: eine Raumzeit, in der (Cusas) Isoperimetrie, geringste Zeit und geringste Aktion auf einheitliche Weise vorherrschen.((Siehe „20. John and Jacob Bernoulli, The Brachystochrone“, A Source Book in Mathematics, 1200–1800, hrsg. von D. J. Struik (Princeton University Press, Princeton, N. J., 1986), S. 391–399.)) Die Riemannsche Oberflächenfunktion und Cantors Aleph-Reihe definieren implizit ein physikalisches Universum, in dem die Existenz nicht-entropischer (d. h. lebender und kognitiver) Prozesse nicht nur erlaubt, sondern notwendig ist. Riemanns Habilitationsschrift, seine Arbeit über Riemannsche Oberflächen, über „ebene Luftwellen“ usw. befassen sich alle mit dieser historischen Entwicklung geometrischer Begriffe unter dem Einfluß von Ideen, die vom Bereich der Physik ausgehen.

Für den Ökonomen ist der entscheidende Punkt, daß wirtschaftliche Prozesse nur innerhalb der letzten der eben genannten Geometriearten ablaufen: der nicht-entropischen Prozesse, des Prozesses der zunehmenden Beherrschung des Universums durch den Menschen pro Kopf, pro Familienhaushalt und pro fraglicher Einheit der Erdoberfläche. Diese Beherrschung bedeutet, daß das Universum, von dem wir hier sprechen, selbst ein nicht-entropischer Prozeß ist. Jede Mathematik, die nicht für derartige nicht-entropische Prozesse geeignet ist, ist von Natur aus inkompetent für wirtschaftliche Analysen.

Die erwähnte Entdeckung des Eratosthenes ebenso wie verwandte Entdeckungen erfordern eine qualitative Änderung der Art und Weise, wie Messungen von Unterschieden auf der Erdoberfläche und auch astronomische Beobachtungen verstanden werden sollten. Die bekräftigenden Meßunterschiede, zu denen wir durch diese so aufgeworfenen Ideen axiomatisch geführt werden, spiegeln die Effizienz einer solchen Entdeckung wider: Der Beweis für jede axiomatisch-revolutionäre oder verwandte Entdeckung ist nicht ihre scheinbare formale Übereinstimmung mit einer bestehenden Mathematik, sondern vielmehr, daß sie die Macht der menschlichen Gattung im Universum erhöht.

Die angeführten Beispiele von Veränderungen in der Mathematik veranschaulichen diesen Punkt. Wie das Beispiel Eratosthenes zeigt, müssen wir, sobald der Beweis für eine Idee erbracht ist, die Axiome der Geometrie so verändern, daß eine neue Mathematik, ein neues Theoremgitter entsteht. Dieser Schritt führt uns in die Mitte der Entdeckung, die Riemann in seiner Habilitationsschrift gemacht hat.

Riemanns Entdeckung

An dieser Stelle muß betont werden, daß die beiden einleitenden Absätze von Riemanns Habilitationsschrift mit dem Untertitel „Plan der Untersuchung“ Äußerungen darstellen, die in ihrer Schärfe, Wucht und Ausrichtung ganz oben unter allen je getroffenen wissenschaftlichen Aussagen stehen.((„Plan der Untersuchung“, in Riemann, Werke, a. a. O., S. 254 f.)) Diese Schärfe spiegelt die Tatsache wider, daß es sich hier um eine der grundlegendsten Entdeckungen der gesamten Wissenschaftsgeschichte handelt. Die sich durch die gesamte Habilitationsschrift ziehende Qualität verlangt, daß das Werk mit klarem Kopf gelesen und studiert werden muß, wie es bis heute nur wenige getan zu haben scheinen: selbst Albert Einstein eingeschlossen, der Riemanns Arbeit lobte.((Trotz des frühen Einflusses von Ernst Machs Positivismus zeigte sich Einstein immer wieder als moralischer und zugleich fähigster Wissenschaftler. Seine Aussage, daß er Bernhard Riemanns Habilitationsschrift wie auch Johannes Kepler Dank schulde, und auch seine spätere Zusammenarbeit mit Kurt Gödel sind dafür bezeichnend. Dieser Ausdruck seiner moralischen Einstellung zur Wissenschaft ist eine beständige Qualität; Einsteins empörte Äußerung („Gott würfelt nicht“) gegenüber der betrügerischen Physik, wie sie sich die Solvay-Konferenzen der 1920er Jahre zu eigen machte, veranschaulicht dies. Seine Moral beruhte auf einem durchgehenden Bekenntnis, daß das Universum einem effizienten Vernunftprinzip folgt, in dem Sinne, wie Platon, Nikolaus von Kues, Kepler, Leibniz, Gauß und Riemann diesem Wissenschaftsprinzip verpflichtet sind. Wie auch in seiner kompetenten Verteidigung von Max Planck gegen die fanatischen positivistischen Anhänger Machs hält er jedoch an dem Punkt inne, wo eine gründliche Widerlegung der Grundannahmen des Empirismus erforderlich wäre.)) Wir wollen nun die entscheidende Bedeutung von Riemanns Entdeckung für die Wirtschaftswissenschaft zusammenfassen und diese anhand der eigenen These des Verfassers darstellen.

Die Mathematik, die gesamte Geometrie eingeschlossen, ist kein Produkt der Sinne, sondern der Vorstellungskraft. In ihrem Hauptbestandteil ist unsere Mathematik in den Ideen der Geometrie verwurzelt; was die meisten, eingeschlossen die professionellen Anhänger der Galileo-Newton-Tradition, für Mathematik halten, leitet sich von einer naiven Vorstellung der einfachen euklidischen Festkörpergeometrie ab. Konzentrieren wir uns nun auf einen enger gefaßten Aspekt des so aufgeworfenen allgemeinen Problems: die Trugschlüsse, die in dem Versuch stecken, mathematische Wirtschaftsmodelle auf Grundlage einer Newtonschen Form der heute allgemein akzeptierten Universitätsmathematik zu entwerfen.

Diese Mathematik leitet sich aus einer speziellen Sicht eines mutmaßlichen euklidischen Raumzeit-Modells ab. Es wird angenommen, daß dies ein ontologisch leerer Raum sei, der durch drei vollkommen kontinuierliche, unendliche Ausdehnungen definiert ist: von oben nach unten, von Seite zu Seite und von vorne nach hinten. In diesem Raum herrscht ein Zeitbegriff, der ebenfalls vollkommen kontinuierlich nur in eine Richtung ausgedehnt ist: rückwärts-vorwärts. Dies läßt sich sinnvollerweise als eine Geometrie verstehen, die aus der naiven Vorstellungskraft stammt. Die vier vollkommen kontinuierlichen unendlichen Ausdehnungen (vierfach ausgedehnte Raumzeit) bilden die charakteristische Hypothese dieser Geometrie als Theoremgitter.

Hinzu kommt eine simplistische Vorstellung von imaginärer physikalischer Raumzeit, die man ansonsten am besten mit „Dinge scheppern herum, wenn man sie in einen ansonsten leeren Eimer füllt“, beschreiben könnte. Gegeben sei ein Objekt, das einer tatsächlichen oder möglichen Sinneswahrnehmung entsprechen soll. Gemäß der Hypothese für einfache Raumzeit läßt sich ein Punkt, dessen wahre Raumzeitgröße absolut Null ist, als Teil dieses Objekts und auch als Ort in einer vierfach ausgedehnten Raumzeit lokalisieren. In Erweiterung dieses Begriffs kann jedes Objekt so abgebildet werden, daß es eine relevante Region der Raumzeit einnimmt; diese Abbildung erfolgt in Form einer großen Dichte solcher Punkte, die dem Objekt und der Raumzeit als Orte gemeinsam sind.

Als nächstes wird angenommen, daß die Bewegung von Objekten auf diese Weise verfolgt werden kann (in vierfach ausgedehnter Raumzeit). Die physikalische Erfahrung zeigt jedoch, daß die Raumzeit allein die Bewegung von Objekten nicht bestimmen kann. Man nimmt an, daß die Variabilität der wahrgenommenen Bewegung dem entspricht, was man als physikalische Attribute bezeichnen könnte, wie Masse, Ladung, Geruch und so weiter. Der Ausdehnungsbegriff kann auf jedes dieser Attribute angewandt werden. Dies führt dazu, daß wir uns die physikalische Raumzeit als mehrfach ausgedehnte Größen vorstellen müssen, und zwar in einer Weise, die allgemeiner ist als die intuitive Vorstellung von einfacher Raumzeit.

Wenn als Teil der Hypothese für das System angenommen wird, daß offenbare Ursache-Wirkungs-Beziehungen mit Einfluß auf die Bewegung in Form einer Vielzahl solcher physikalischen Ausdehnungsfaktoren adäquat ausgedrückt werden können, läßt sich ein solcher Versuch, eine physikalische Raumzeit zu konstruieren, als eine physikalische Raumzeit-Mannigfaltigkeit beschreiben. Diese Geometrie der naiven Vorstellung ist die Übersichtskarte für die empiristische mathematische Physik von Paolo Sarpi und seinen Anhängern wie Galileo Galilei, Francis Bacon, Thomas Hobbes, René Descartes, Isaac Newton, Leonhard Euler, Lord Rayleigh und so weiter.((Siehe Diskussion über Sarpi und seine Anhänger, in Lyndon H. LaRouche jr., „Why Most Nobel Prize Economists Are Quacks“, Executive Intelligence Review, Vol. 22, Nr. 30, 28. Juli 1995, passim.))

Dieser simplistische Ansatz an die mathematische Physik ist die eigentliche Grundlage für die derzeit allgemein akzeptierten Vorstellungen über Ökonomie sowohl innerhalb des Berufsstandes als auch unter Laien. Diese mechanistische Newtonsche Sicht ist ansonsten das verbreitete Mißverständnis des Begriffs „Wissenschaft“ selbst. Hierauf geht auch der Kantsche Ausdruck von „wissenschaftlicher Objektivität“ zurück.

Riemann greift diese Überlegung in den beiden einleitenden Absätzen seiner Habilitationsschrift auf und attackiert damit die Probleme dieser naiven Geometrie selbst:

„Bekanntlich setzt die Geometrie sowohl den Begriff des Raumes, als die ersten Grundbegriffe für die Constructionen im Raume als etwas Gegebenes voraus. Sie giebt von ihnen nur Nominaldefinitionen, während die wesentlichen Bestimmungen in Form von Axiomen auftreten. Das Verhältniss dieser Voraussetzungen bleibt dabei im Dunkeln; man sieht weder ein, ob und wie weit ihre Verbindung nothwendig, noch a priori, ob sie möglich ist.

Diese Dunkelheit wurde auch von Euklid bis Legendre, um den berühmtesten neueren Bearbeiter der Geometrie zu nennen, weder von Mathematikern, noch von den Philosophen, welche sich damit beschäftigten, gehoben.… Hiervon aber ist eine notwendige Folge, daß die Sätze der Geometrie sich nicht aus allgemeinen Grössenbegriffen ableiten lassen, sondern daß diejenigen Eigenschaften, durch welche sich der Raum von anderen denkbaren dreifach ausgedehnten Größen unterscheidet, nur aus der Erfahrung entnommen werden können.“((Riemann, Werke, a. a. O., S. 254 f.))

Oder, wie Riemann sich am Ende seiner Habilitationsschrift ausdrückt: innerhalb „des Gebiets der Physik“ und nicht der Mathematik an sich.((ebenda, S. 268.))

Die erste mathematische Herausforderung, die sich aus der allgemeinen Idee einer physikalischen Raumzeit-Mannigfaltigkeit ergibt, besteht darin, daß eine solche Idee alle Vorstellungen einer statischen Geometrie ausschließt. Seit Ende des letzten Jahrhunderts wurde häufig darauf verwiesen, daß, wenn man die Tatsache berücksichtigt, daß sich die Variabilität der Bewegungsgeschwindigkeiten selbst einfacher Objekte nicht auf einige bloße Raumzeit-Prinzipien reduzieren läßt, die bloße Vorstellung von Raum und Zeit aus der mathematischen Physik ausgeschlossen werden müßten.((Diese Frage wurde bereits in den 1690er Jahren von Leibniz und Jean Bernoulli auf eigene Weise formuliert. Als Christiaan Huyghens 1677 erfuhr, daß sein ehemaliger Schüler Ole Rømer im Jahr zuvor für die „Lichtgeschwindigkeit“ einen Wert von etwa 3 · 10⁸ Metern pro Sekunde angegeben hatte, erkannte Huyghens sofort, welche Auswirkungen eine konstante Geschwindigkeit retardierter Lichtausbreitung auf Reflexion und Brechung hätte. Siehe Poul Rasmussen, „Ole Rømer and the Discovery of the Speed of Light“, 21st Century Science & Technology, Bd. 6, Nr. 1, Frühjahr 1993. Siehe auch Christiaan Huyghens, Abhandlung über das Licht, 1678, Verlag von Wilhelm Engelmann, Leipzig, 1890. Leibniz‘ Angriffe auf die Untauglichkeit der von Newton verwendeten algebraischen Methode für die Physik und sein Verständnis für die Notwendigkeit einer „nicht-algebraischen“ (d. h. transzendentalen) Methode spiegelten somit am deutlichsten den erwiesenen Grundsatz von Lichtreflexion und -brechung in Einklang mit einer konstanten Rate der retardierten Ausbreitung wider – unabhängig von den Vorstellungen, die im Hinblick auf eine naive physikalische Raumzeit möglich sind.)) Da sich unsere Mathematik aus dem dreifachen Raum unserer Vorstellung ableitet, wie soll die Physik mathematisch die Verzerrung erklären, die die nachweisliche physikalische Raumzeit-Mannigfaltigkeit für die Möglichkeit bedeutet, Bewegung in der Raumzeit darzustellen?

Unterbrechen wir kurz die Beschreibung von Riemanns Habilitationsschrift, um dem Leser mitzuteilen, daß wir uns in den nächsten Absätzen nicht mit allen entscheidenden Punkten der Habilitationsschrift befassen werden, aber mit einigen, die sich alle implizit auf die Probleme der „Wirtschaftsmodellierung“ beziehen; mit einem davon am ausdrücklichsten.

Bei der Behandlung der ersten Fragestellung, dem Begriff einer nfach ausgedehnten Größe,((Riemann, „I. Begriff einer nfach ausgedehnten Größe“, a. a. O., Werke, S. 255 ff.)) stellt Riemann fest, daß er nur zwei Literaturquellen gefunden habe, die ihm dabei geholfen hätten: Gauß‘ zweite Abhandlung über biquadratische Reste((C. F. Gauß, „Zur Theorie der biquadratischen Reste, zweite Abhandlung“, Werke, a.a.O., Band II, S. 93–148.)) und eine philosophische Untersuchung von Johann Friedrich Herbart.((J. F. Herbart war ein bekannter Gegner der Philosophie Immanuel Kants. Er geriet unter den Einfluß des Geschichtsprofessors Friedrich Schiller an der Universität Jena und später von Wilhelm von Humboldt an der Universität Königsberg, wo er auf Kants ehemaligen Lehrstuhl berufen wurde. Mitte der 1830er Jahre wurde Herbart auf Betreiben von C. F. Gauß an die Göttinger Universität berufen, wo er eine berühmte Vorlesungsreihe hielt. In diesem Zusammenhang kam Riemann erstmals mit ihm in Kontakt. Riemanns kritische Anmerkungen auf einige von Herbarts Argumenten enthalten das Material, auf das an dieser Stelle in seinen „Hypothesen“ Bezug genommen wird; siehe Riemann, „I. Zur Psychologie und Metaphysik“, Werke, S. 480–488.))

Im einleitenden Absatz des nächsten Unterkapitels über die Maßverhältnisse((Riemann, „Massverhältnisse, deren …“, a. a. O., Werke, S. 258.)) stellt er dann einen entscheidenden Punkt fest, auf den sich unsere Aufmerksamkeit konzentrieren wird:

„Es wird daher, um festen Boden zu gewinnen, zwar eine abstrakte Untersuchung in Formeln nicht zu vermeiden sein, die Resultate derselben aber werden sich im geometrischen Gewande darstellen lassen… [S]ind die Grundlagen enthalten in der berühmten Abhandlung des Herrn Geheimen Hofraths Gauß über die krummen Flächen.“((ebd. Riemann bezieht sich auf eine der berühmtesten und einflußreichsten Entdeckungen von C. F. Gauß, die durch die Probleme der Speziellen Relativitätstheorie doppelt berühmt wurde. Gauß‘ zusammenfassende Arbeit zu diesem Thema wurde ursprünglich 1828 in lateinischer Sprache unter dem Titel „Disquisitiones Generales Circa Superficies Curvas“ (in C. F. Gauß, Werke, a. a. O., Band 4, S. 217–258 veröffentlicht (auf deutsch herausgegeben unter dem Titel „Allgemeine Flächentheorie“ von A. Wangerin, Verlag von Wilhelm Engelmann, Leipzig, 1889). Es wäre jedoch nützlich, auch Gauß‘ „Theorie der krummen Flächen“ (ebd., Band 8, S. 368–452) zu lesen.))

Möge der Ausdruck, daß sich die Resultate „im geometrischen Gewand darstellen lassen“, in unseren folgenden Überlegungen seine Resonanz finden.

Als der Verfasser 1952 Riemanns Habilitationsschrift im Lichte von Cantors Aleph-Transfiniten erneut las, bestanden seine eigenen relevanten „Maßverhältnisse“ bereits in dem gleichen Maßprinzip, das in der gleichen allgemeinen Konzeption der hier beschriebenen physikalisch-ökonomischen „Nicht-Entropie“ subsumiert ist. Definieren wir die „Nicht-Entropie“ eines physikalischen (makro-)ökonomischen Prozesses in den oben verwendeten allgemeinen Begriffen. Befassen wir uns mit den folgenden vorbereitenden Schritten, die erforderlich sind, um die Bedeutung der auf einen solchen wirtschaftlichen Prozeß anwendbaren „Maßverhältnisse“ breit zu definieren.

Bestimmen wir einen kleinen, aber bedeutsamen Quotienten der „freien Energie“, etwa einen Wert von 5 %. In diesem Quotienten sind die folgenden Ungleichheiten enthalten:

• Die potentielle relative Bevölkerungsdichte muß steigen;
• die demographischen Eigenschaften der Familienhaushalte und der Bevölkerung insgesamt müssen sich verbessern;
• die Kapital- und Energieintensität, gemessen in physischen Größen, muß pro Kopf, pro Haushalt und pro Einheit der relevanten Landfläche zunehmen;
• ein Teil der „freien Energie“, der ausreicht, um einen Anteil von konstant nicht weniger als 5 % freie Energie aufrechtzuerhalten, muß in den Produktionszyklus reinvestiert werden, um die Kapitalintensität, die Energieintensität und den Umfang des Produktionsprozesses zu erhöhen [siehe die Darstellung der auf die Realwirtschaft anwendbaren Maßverhältnisse am Ende dieses Artikels].

Die Forderung nach einem konstanten Wachstumsfaktor von 5 % dient als Faustregel, um sicherzustellen, daß die Wachstumsspanne ausreicht, um zu verhindern, daß der Prozeß als Ganzes in eine entropische Phase übergeht.

Das sind die für erfolgreiche Volkswirtschaften charakteristischen effektiven Maßverhältnisse. Wenn man diese Maßverhältnisse übernimmt, auf welche Art physikalische Raumzeit beziehen wir uns dann implizit? Schauen wir zurück in die Frühgeschichte der modernen Wissenschaft; dort stößt man auf einige nützliche Anregungen.

In dem Gründungswerk der modernen Wissenschaft, der De docta ignorantia, führte Nikolaus von Kues den Begriff in Form eines sich selbst erhaltenden Prozesses, des isoperimetrischen Prinzips, ein, um die Axiome von Punkt und Gerade zu ersetzen. Dieses isoperimetrische Prinzip, in Gestalt der Zykloide der verallgemeinerten Lichtbrechung, wurde mit den Begriffen „geringste Wirkung“, „geringste Zeit“ und „geringste Einschränkung“ assoziiert. Von den erwähnten Arbeiten von Rømer und Huyghens bis zu Jean Bernoulli und Leibniz und darüber hinaus diente das Prinzip der retardierten Lichtausbreitung in Verbindung mit dem isoperimetrischen Prinzip usw. als Maßstab, als „Uhr“ des relativen Werts für die Naturwissenschaft im allgemeinen. Dies angemerkt, definiere man nun die Bewegung eines nicht-entropischen wirtschaftlichen Prozesses relativ zu dem von der „Uhr“ gelieferten Maß.

Entsprechend dieser „Uhr“ messen wir in erster Näherung die Verhältnisse von Produktion und Konsum in Gesellschaften, die als integrierte Ganzheiten betrachtet werden. Dies ist ein statistischer Anfang, aber noch nicht der erforderliche Maßstandard. Diese ersten Schätzungen müssen in einer zweiten Näherung in Form von Änderungsraten der Produktions- und Konsumverhältnisse ausgedrückt werden, die wiederum als Wachstumsraten der potentiellen relativen Bevölkerungsdichte ausgedrückt werden müssen.

Dies wiederum erfordert eine erneute Überprüfung des Begriffs der wirtschaftlichen Nicht-Entropie. Der Inhalt der Nicht-Entropie wird nicht anhand des zahlenmäßigen Anstiegs der Warenkorbobjekte und des Verhältnisses von Produktion und Konsum gemessen. Vielmehr hängt die Aussagekraft von Versuchen, die Wertentwicklung der Warenkörbe zu messen, davon ab, ob diese Berechnungen mit der Zunahme der potentiellen relativen Bevölkerungsdichte einhergehen. Mit anderen Worten, die wirtschaftliche Nicht-Entropie, wie wir ihre statistische Annäherung oben beschrieben haben, muß mit der Zunahme der potentiellen relativen Bevölkerungsdichte parallel gehen. Es ist die Zunahme der potentiellen relativen Bevölkerungsdichte als solcher, die den ontologischen Gehalt der veranschlagten Nicht-Entropie ausmacht.

Anstatt also Entfernung in der realwirtschaftlichen Raumzeit in Zentimeter-Gramm-Sekunde oder analogen Einheiten zu messen, messen wir den nicht-entropischen Effekt als Zunahme der potentiellen relativen Bevölkerungsdichte. Der Wert des Vorgangs wird implizit in letzterer Maßeinheit ausgedrückt. Wie wir bereits eingangs geschrieben haben: Es ist der implizite soziale Inhalt jeder gültigen axiomatischen revolutionären Entdeckung in Wissenschaft oder Kunst, der das menschliche Wissen definiert – nicht Norbert Wieners mechanistischer, statistischer Ansatz. Dieser implizite soziale Inhalt drückt die Wirksamkeit der praktizierten Ideen aus, mit dem Effekt, daß die Zuwachsrate der potentiellen relativen Bevölkerungsdichte der Gesellschaft beibehalten und auch erhöht wird.

Betrachten wir, wie sich die soeben zusammengefaßten Punkte auf die Mathematik auswirken.

Der erste Schritt bei der Konstruktion einer „realwirtschaftlichen Raumzeit-Mannigfaltigkeit“ besteht darin, die zählbaren Warenkategorien zu verwenden, die für solche statistischen Studien angezeigt sind. Der zweite Schritt besteht darin, mit Hilfe dieser Datenbank ein Mittel zur Messung der Beziehungen innerhalb des Systems in bezug auf die veranschlagte relative Nicht-Entropie des laufenden Wirtschaftsprozesses als ein integriertes Ganzes zu erhalten. Der dritte Schritt besteht darin, die Rate der Nicht-Entropie zu veranschlagen, die durch einen Vergleich mit der Rate der Nicht-Entropie, ausgedrückt als potentielle relative Bevölkerungsdichte, überprüft und korrigiert wird. Die Ergebnisse des dritten Schritts müssen als Korrektur für die zuvor im zweiten Schritt veranschlagten Standards verwendet werden; diese letztere Korrektur muß wiederum auf die Bewertung der im ersten Schritt verwendeten statistischen Kategorien zurückwirken. Riemanns Arbeit bietet einen konzeptionellen Leitfaden für dieses vielschichtige Unterfangen.

Indem wir festlegen, daß die Maßverhältnisse in der realwirtschaftlichen Raumzeit durch die Zuwachsrate der potentiellen relativen Bevölkerungsdichte bestimmt werden, haben wir die mathematische Darstellung wirtschaftlicher Prozesse in den Bereich der nicht-euklidischen Geometrie übertragen, wie der Begriff einer solchen Geometrie in Riemanns Habilitationsschrift definiert ist. Das heißt, wir haben in die Graphiken, die wir unter Verwendung geeigneter Marktkorbdaten anfertigen können, unseren Meßstandard eingebracht.

Zu Eratosthenes‘ Zeiten war die Erde für das Auge des Beobachters flach, und deshalb mußte sie nach den damaligen Prinzipien der ebenen Geometrie gemessen werden. Indem Eratosthenes zeigte, daß diese Meßmethode zu verheerenden Widersprüchen führte, wenn man sie auf bestimmte Weise betrachtete, wurde es erforderlich, daß er Prinzipien verwendete, die später als Gesetze der Geodäsie bekannt wurden – Prinzipien, die für das Messen auf gekrümmten Oberflächen galten und nicht mehr den Grundsätzen der ebenen Geometrie entsprachen.

Wie oben bereits bemerkt: Später, im letzten Viertel des 17. Jahrhunderts, als durch die astronomischen Forschungen Ole Rømers eine bestimmte Geschwindigkeit für die retardierte Ausbreitung des Lichtes festgelegt war, stellte sich durch die Arbeiten von Huyghens, Leibniz und Jean Bernoulli die Notwendigkeit heraus, die naive Form der perfekt kontinuierlichen euklidischen Raumzeit von Sarpi und Galileo durch eine physikalische Raumzeit mit fünffacher Ausdehnung zu ersetzen, eine Raumzeit, die nach Leibniz nicht perfekt kontinuierlich war.((Darum drehte sich der berüchtigte Angriff des Newton-Anhängers Leonhard Euler auf Leibniz‘ Monadologie im Jahre 1761. Siehe Lyndon H. LaRouche jr., „Appendix XI: Euler’s Fallacies on the Subjects of Infinite Divisibility and Leibniz’s Monads“, The Science of Christian Economy, Schiller Institute, Washington, D.C., 1991, S. 407–425.)) Neben der vierfachen Ausdehnung von Raum und Zeit muß die Geschwindigkeit der verzögerten Lichtausbreitung als weitere Ausdehnung hinzugefügt werden. Um dem gerecht zu werden, mußte Cusas Vorstellung übernommen werden, daß die Idee des dreifach ausgedehnten Raumes dem untergeordnet ist, was später als transzendentaler Bereich bezeichnet wurde, worin das isoperimetrische Prinzip und nicht axiomatische Punkte und Linien die zugrunde liegende Hypothese definiert.

Und so weiter, in der Geschichte seit damals.

In dieser Tradition sind wir mit Hilfe von Riemanns Arbeit in der Lage, den geometrischen Schatten der entsprechenden nfachen physikalischen Raumzeit-Mannigfaltigkeit der physikalischen Ökonomie als Abbild in einem dreifach ausgedehnten Bereich darzustellen. Das ist, als wollte man mit dem damals 27jährigen Riemann sagen,((Riemann wurde am 17. September 1826 geboren, Werke, S. 509; die Verlesung seiner Habilitationsschrift erfolgte am 10. Juni 1854, ebenda, S. 254).)) daß „eine abstrakte Untersuchung in Formeln nicht zu vermeiden sein wird, die Resultate derselben aber werden sich im geometrischen Gewande darstellen lassen“. Als wesentliche Bedingung sollten wir nie vergessen, daß wir genau das getan haben.((Würde man diesen Umstand Studenten und anderen „Konsumenten“ von ökonomischen Arbeitsergebnissen nicht verdeutlichen, so würde das Ergebnis tendenziell zu dem Aberglauben führen, der für die meisten mit dem Nobelpreis ausgezeichneten Ökonomen und ihre Nacheiferer typisch ist. Was wir wissen, ist das, wofür wir in der Art und Weise, wie wir es in Erfahrung gebracht haben, Rechenschaft ablegen können.))

Um den wichtigen Beitrag Riemanns in dem für unsere Zwecke erforderlichen Umfang zu verstehen, müssen wir in der ganz besonderen Art und Weise zu Riemann zurückkehren, wie der Autor Riemanns Habilitationsschrift im Jahre 1952 erneut gelesen hat. Wir müssen unser Augenmerk auf die Besonderheit jener tieferen Erkenntnis über Riemanns Entdeckung richten, die durch das Studium von Cantors Werk durch den Autor ausgelöst wurde.

Dichte von Unstetigkeiten

Seine Beiträge …((Georg Cantor, „Beiträge zur Begründung der transfiniten Mengenlehre“, a. a. O.)) enthalten Georg Cantors wichtigsten formalen Beitrag zur Mathematik. Seine wichtigsten Darstellungen über die Philosophie der Mathematik entstanden in Schriften Mitte der 1880er Jahre, vom Erscheinen seiner Grundlagen …((Georg Cantor, „Grundlagen einer allgemeinen Mannigfaltigkeitslehre“, Leipzig: 1883. Ursprünglich veröffentlicht als „Über unendliche lineare Punktmannigfaltigkeiten“, Abhandlungen, a. a. O., S. 139–246.)) (1883) bis fast ein Jahrzehnt vor seinen Beiträgen …((Siehe Anmerkung 4.)) (1897). Dazu gehört eine Reihe von Mitteilungen über die historischen, philosophischen und methodischen Implikationen des Begriffs transfinit. Von den Grundlagen an beschäftigte sich Cantor in dieser Zeit vor allem mit formalen Fragen des mathematischen Transfiniten, aber auch, wenn nur beiläufig, mit dem ontologischen Transfiniten.((Z. B. „Mitteilungen zur Lehre vom Transfiniten“, Abhandlungen, a. a. O., S. 378–440.))

Kurz gesagt, im Zusammenhang mit seinen historisch-philosophischen Betrachtungen deckt sich Cantors Begriff des Transfiniten ganz mit Platons ontologischem Begriff des Werdens, und sein Begriff des mathematischen Absoluten stimmt mit Platons ontologischer Konzeption des Guten überein. Wendet man dies auf Riemanns Entdeckung an, sind die relevanten Fragen insgesamt in Platons Parmenides-Dialog enthalten. Dabei geht es um folgendes.

Im Parmenides-Dialog wird Parmenides, der Hauptvertreter der reduktionistischen Eleaten-Schule, von Platons Sokrates geschickt dazu gebracht, die unvermeidlichen und axiomatisch eindeutigen Paradoxe des eleatischen Dogmas selbst offen zu legen. Das Paradox ist formal wie auch ontologisch, vor allem aber ontologisch. Im Dialog selbst liefert Platon nur einen ironischen, beiläufigen Hinweis auf die Lösung des Paradoxes: Parmenides hat das Prinzip der Veränderung außer Acht gelassen. Es gibt aber eine direkte funktionale Beziehung von Platons implizitem Argument zu Riemanns Entdeckung; Cantors Verweise auf Platons Werden und das Gute sind für beide unmittelbar relevant. Einen wichtigen Hinweis auf diese Zusammenhänge liefert Riemann selbst in einem posthum veröffentlichten, gegen Kant gerichteten Dokument mit dem Titel „Zur Psychologie und Metaphysik“.((Riemann, Werke, S. 477–488. Mein Kollege, Dr. Jonathan Tennenbaum, hat sich zu C. F. Gauß‘ vernichtendem Hohn über Kants Werk geäußert. Cantor drückt in den Mitteilungen eine ähnliche Verachtung für Kant aus.))

Die gemeinsamen Verbindungen haben im wesentlichen die folgenden bedeutsamen Aspekte.

Beziehen wir uns auf den erwähnten allgemeinen Fall einer Reihe von Theoremgittern, betrachtet im Rahmen einer Abfolge, die der Zunahme der potentiellen relativen Bevölkerungsdichte einer Kultur entspricht. Wir haben es also mit einem Gitter von Theoremgittern zu tun, die jeweils durch eine oder mehrere absolute, logisch-axiomatische Unstetigkeiten (z. B. mathematische Unstetigkeiten) voneinander getrennt sind. Frage: Was ist die Ordnungsbeziehung zwischen den Gliedern eines solchen Gitters von Theoremgittern? Man betrachte dies als ein potentielles ontologisches Paradox, wie es in Platons Parmenides behandelt wird.

Einige Entdeckungen können in der Realität entweder vor oder nach bestimmten anderen Entdeckungen auftreten; sie müssen jedoch immer nach einigen Entdeckungen und vor einigen anderen auftreten. Dies gilt sowohl für Entdeckungen in den klassischen Kunstformen und verwandten Bereichen als auch für naturwissenschaftliche Entdeckungen. Mit anderen Worten, jede gültige axiomatisch-revolutionäre Entdeckung im menschlichen Wissen läßt sich als ein Glied des Gitters von Theoremgittern identifizieren; es existiert nur durch einen notwendigen Vorgänger und ist selbst ein notwendiger Vorgänger anderer Glieder. Dies ist die historische Realität des bisher angehäuften gültigen Wissensfortschritts der menschlichen Gattung als Ganzer. Dies ist, aus den oben umfassend genannten Gründen, die Funktion, mit der sich die Ursache der sukzessiven Zunahme der potentiellen relativen Bevölkerungsdichte der Menschheit aufsuchen läßt. Frage: Welches ist das Ordnungsprinzip, das alle denkbaren Glieder dieses Gitters von Theoremgittern in sich fassen könnte?

Auf der relativ einfacheren Ebene ist die Lösung des im Parmenides dargestellten Paradoxes voraussagbar, wenn die untersuchte Gliederabfolge von einer bestimmten Qualität ist. Wenn sich der Bestand an Gliedern als geordnete Reihe oder geordnetes Gitter ausdrücken läßt, können entweder alle Glieder oder zumindest einige von ihnen beschrieben werden, als wenn sie durch ein konstantes Ordnungsprinzip, einen konstanten Differenz-(Änderungs-)Begriff zwischen den Gliedern, erzeugt wurden. In diesem Fall kann der einzelne Differenz-(Änderungs-)Begriff durch einen Begriff für jedes einzelne Glied des Bestandes ersetzt werden. Im Sinne des Platon-Dialogs kann also das Viele durch das Eine dargestellt werden.

In seinem Hauptwerk konzentriert sich Cantor darauf, das Viele einer unendlich ausgedehnten mathematischen Reihe durch das Eine darzustellen. Seine Behandlung mathematischer Mächtigkeiten (Kardinalitäten) in diesem Bezugssystem führt zum Begriff der höheren transfiniten Zahlen, den Alephs, und zum allgemeinen Begriff des Zählens in bezug auf Mächtigkeiten als solchen. Letzteres entspricht am deutlichsten der Dichte formaler Unstetigkeiten im Vergleich von gültigen axiomatisch-revolutionären Entdeckungen. Frage: Wie soll letzteres Vieles durch ein konstruierbares oder anderweitig erkennbares Eines dargestellt werden?

Der Begriff, der mit der Lösung dieser Aufgabe verbunden ist, findet sich bereits im Werk Platons: der Begriff der höheren Hypothese. Verwendet man jedoch die Formulierung aus Riemanns Dissertation, der Konzeptualisierung dieser Lösung, wird die tatsächliche Kenntnis des Begriffs der höheren Hypothese als ontologischer Aktualität „nur aus der Erfahrung entnommen werden können“.

Nehmen wir als Beispiel einen Studenten, der eine klassisch-humanistische Erziehung durchlaufen hat, in der das Nacherleben eines ursprünglichen axiomatisch-revolutionären Entdeckungsaktes der einzige akzeptierte Standard für Wissen ist. Dieser Student hat die wiederholte Erfahrung gemacht, ein Entdeckungsprinzip anzuwenden, das regelmäßig zu gültigen axiomatisch-revolutionären Entdeckungen führt. Diese wiederholte Erfahrung, dieser rekonstruierte mentale Entdeckungsakt, ist zu einem der bewußten Reflexion zugänglichen Objekt geworden – einer Idee, einem Denkobjekt. Wie jedes solche Denkobjekt läßt sich dieser Geisteszustand abrufen und auch bewußt einsetzen. Wie sollte man diese Qualität – diesen Typ((„Typ“ im Sinne Cantors.)) – von Gedankenobjekten nennen?

So wie Platon eine gültige neue Reihe voneinander abhängiger Axiome, die einem entsprechenden Theoremgitter zugrunde liegen, als Hypothese bezeichnet, so verweist er auf den Typ des Gedankenobjekts, auf den wir gerade Bezug genommen haben, als höhere Hypothese. Der Umstand, daß die Art und Weise, wie man zu gültigen axiomatisch-revolutionären Hypothesen gelangt, selbst verbessert werden kann, bedeutet eine mögliche Reihe von Übergängen zu sukzessiv besseren (leistungsfähigeren) Qualitäten der höheren Hypothese, ein Zustand geistiger Aktivität, den Platons Methode als Hypothese der höheren Hypothese kennt. Letztere deckt sich mit Cantors allgemeiner Vorstellung des Transfiniten: mit anderen Worten, Platons ontologischer Zustand des Werdens.((Es ist nicht erforderlich, im vorliegenden Zusammenhang über das Gute zu sprechen. Vgl. dazu Lyndon H. LaRouche jr., „The Truth About Temporal Eternity“, Fidelio, Sommer 1994, passim.))

In seiner posthum veröffentlichten Schrift „Zur Psychologie und Metaphysik“ faßt Riemann „Hypothese“ wie auch „höhere Hypothesen“ zu einer Gattung zusammen, die er Geistesmassen nennt. Dieser Begriff ist gleichbedeutend mit der Leibnizschen „Monade“ und dem vom Verfasser bevorzugten Begriff „Gedankenobjekt“: Ideen, die den hier betrachteten formalen Unstetigkeiten entsprechen. Jeder Mensch, der wiederholt gültige axiomatisch-revolutionäre Entdeckungen in der genannten klassisch-humanistischen Art und Weise nacherlebt hat, ist mit der Existenz solcher Ideen vertraut.

Damit zurück zu Platons Parmenides. Betrachten wir den Fall, daß das Prinzip der Veränderung, das Eine, das die Erzeugung der Glieder des Bestandes, das Viele, ordnet, die Form einer höheren Hypothese hat. Dies ist der Fall, wenn die als Vieles bezeichneten Glieder des Bestandes jeweils gültige axiomatisch-revolutionäre Entdeckungen darstellen. Im Gegensatz zu Kants Kritiken((Kritik der reinen Vernunft (1781), Prolegomena zu einer jeder zukünftigen Metaphysik (1783), Kritik der praktischen Vernunft (1788) und Kritik des Urteils (1790).)) ist das Prinzip gültiger axiomatisch-revolutionärer Entdeckungen wißbar, und zwar aus der hier bereits identifizierten Sichtweise.

Ebenfalls im Gegensatz zu Kants notorischen Kritik des Urteils gilt für die klassischen Formen künstlerischen Schaffens dasselbe Prinzip, ebenso wie in der Entwicklungsgeschichte der Methode der Motivführung. Entdeckungen, die sich in dieser Form der Kreativität ausdrücken, sind vor allem mit Mozart (1782–86) und mit Beethovens Revolution in der Motivführung verbunden, vor allem mit seinen späten Streichquartetten.((Siehe Lyndon H. LaRouche jr., „Mozart’s 1782–1786 Revolution in Music“, Fidelio, Winter 1992, und Bruce Director, „What Mathematics Can Learn From Classical Music“, Fidelio, Winter 1994. Die späten Beethoven-Streichquartette, auf die verwiesen wird, sind: Es-Dur, Opus 127; B-Dur, Opus 130; a-Moll, Opus 132; B-Dur („Große Fuge“), Opus 133; und F-Dur, Opus 135.)) Johannes Brahms ist ebenfalls ein Meister dieser Methode kohärenter musikalischer Kreativität.

Die unmittelbar vorhergehenden Beobachtungen dienen dazu, den Begriff einer nachvollziehbaren Ordnung eines Gitters von Theoremgittern verständlich zu machen. In Hinsicht auf die wirtschaftstheoretischen Implikationen von Riemanns Habilitationsschrift sei hier hinzugefügt, daß dieser Begriff nicht nur immanent wißbar ist. Er ist ein physikalisch wirksamer Begriff, der in diesem Sinne ontologisch ist. Er ist auch ontologisch in dem Sinne, wie er bereits von Heraklit und Platon benutzt wurde.

Die Frage ist somit mindestens so alt wie diese beiden Griechen der Antike.

Sobald die ontologische Frage von Platons Parmenides berücksichtigt wird, stellt sich implizit die folgende Frage. Das subsumierende Eine ist ein perfekter Ausdruck für den Bereich, der durch das subsumierte Viele dargestellt wird. Bedeutet folglich die ontologisch inhärente, relative Unvollkommenheit des Vielen, daß die ontologische Aktualität im Einen liegt und nicht in den besonderen Phänomenen oder Ideen des Vielen? Im Verhältnis zu den Besonderheiten im Bereich des Vielen birgt das Eine immer Veränderung in sich. Bedeutet dies, daß Veränderung ontologisch primär ist, relativ zum Inhalt sämtlicher Bereiche des Vielen? Mit anderen Worten, läßt sich hier die ontologische Bedeutung von Heraklits Satz: „Nichts ist beständig, nur der Wandel“, anwenden?

Diese Bedeutung nimmt der Begriff „ontologisch transfinit“ an, wenn man ihn auf die formal oder geometrisch transfiniten Ordnungen anwendet, die von Cantor und in Riemanns Habilitationsschrift dargestellt wurden.

Stellen wir die gleiche Aussage in den Kontext realwirtschaftlicher Prozesse.

Möge der Begriff „Gitter von Theoremgittern“ für eine Reihe von Theoremgittern stehen, die durch ein konstantes Prinzip axiomatisch-revolutionärer Entdeckungen erzeugt wird: eine höhere Hypothese. Dann ist diese höhere Hypothese das Eine, die das Viele der Theoremgitter in sich faßt. Bezogen auf jedes einzelne Glied all dieser Theoremgitter ist diese höhere Hypothese anscheinend die effiziente Ursache für die in der Praxis erzeugte Nicht-Entropie. Es ist diese höhere Hypothese, die (wieder: anscheinend) die relativ primäre, effiziente Ursache der Nicht-Entropie ist. Es ist diese höhere Hypothese, die relativ primär ontologisch ist.

Wie Leonhard Euler und später auch Felix Klein((Felix Klein, Vorträge über ausgewählte Fragen der Elementargeometrie, Leipzig: Teubner 1895, passim. Klein ist sich wahrscheinlich bewußt, daß der Beweis, daß π transzendental ist, vom Standpunkt der Geometrie aus betrachtet zuerst von Nikolaus von Kues erbracht wurde; er weiß ohne Frage, daß der transzendentale Charakter von π von Leibniz et al. in den 1690er Jahren schlüssig nachgewiesen wurde. Dennoch besteht er darauf, daß die Transzendenz von π erstmals 1882 von F. Lindemann nachgewiesen wurde! Der Grund für Kleins dezenten Betrug ist, daß er Eulers Angriff auf Leibniz in der Frage der „unendlichen Reihen“ verteidigt. Kleins Beweggrund ist somit sein Beharren auf einem auf Euler basierenden algebraischen „Beweis“ (und keinem anderen!), selbst auf Kosten eines ungeheuerlichen Betrugs an der Wissenschaftsgeschichte.)) sich zu berücksichtigen weigerten: Korrelation, selbst eine erstaunlich genaue Korrelation, ist nicht unbedingt die Ursache. Die Ursache liegt nicht in der formalen Nicht-Entropie eines solchen Gitters von Theoremgittern; die Ursache drückt sich in den souveränen, schöpferischen Geisteskräften jedes einzelnen Menschen aus: dem entwicklungsfähigen Potential, axiomatisch-revolutionäre Entdeckungen in Wissenschaft und klassischen Kunstformen zu erzeugen, aufzunehmen, zu reproduzieren und wirksam umzusetzen. Dieser aus der „Erfahrung“ stammende Kausalitätsbegriff ist der springende Punkt der Bestimmung einer Riemannschen physikalisch-ökonomischen Raumzeit.

Der Umstand, daß die Menschheit fähig ist, nach oben gerichtete Phasenverschiebungen in der potentiellen relativen Bevölkerungsdichte zu erzeugen, zeigt, daß das Universum so strukturiert ist, daß das entwicklungsfähige schöpferisch-geistige Potential des menschlichen Geistes dieses Universum mit zunehmender Effizienz zu beherrschen in der Lage ist. Allein schon aus diesem Grund ist die Vorstellung „wissenschaftlicher Objektivität“ ein Betrug, insbesondere wenn sie als empirische oder „materialistische“ Vorstellung in Erscheinung tritt. Alles Wissen ist im wesentlichen subjektiv; alle Beweise sind letztlich subjektiv. Quelle des Wissens ist unsere kritische Überprüfung jener geistigen Prozesse, durch die gültige axiomatisch-revolutionäre Entdeckungen erzeugt oder ihre ursprüngliche Erzeugung repliziert werden. Der axiomatisch-revolutionäre wissenschaftliche und künstlerische Fortschritt bei der Erhöhung der potentiellen relativen Bevölkerungsdichte der Menschheit zeigt, daß dies einen gültigen Erkenntnisanspruch darstellt, zumindest relativ gesehen. Erst durch die kritische Selbstüberprüfung der individuellen Geistesprozesse, durch die solche Entdeckungen erzeugt und ihre Erzeugung reproduziert werden, wird wahres wissenschaftliches Wissen erlangt – bzw. das, was sich daher besser als „wissenschaftliche Subjektivität“ bezeichnen ließe.

Insbesondere können gültige axiomatisch-revolutionäre Entdeckungen nicht explizit „kommuniziert“ werden. Sie lassen sich in der Vorstellung anderer nur dadurch wieder zum Vorschein bringen, daß die andere Person dazu veranlaßt wird, den Prozeß des ursprünglichen Entdeckungsaktes nachzuvollziehen. Man mag das Kommunikationsmedium bis in alle Ewigkeit durchsuchen und niemals eine Spur der ursprünglichen Mitteilung einer solchen Idee an irgendeine Person finden. Was kommuniziert wird, ist der Katalysator, der den Hörer dazu veranlaßt, die entsprechenden Erzeugungsprozesse innerhalb seiner eigenen völlig autonomen kreativ-geistigen Prozesse zu aktivieren. Das Ergebnis mag dem „Informationstheoretiker“ als der größte Geheimcode des Universums erscheinen: Tatsächlich wird auf diesem Wege, dem Weg einer klassisch-humanistischen Erziehung, weit mehr „Information“ übermittelt, als sich über den Bandbreitenfilter leiten ließe.

Daher das Folgende:

1. Ursache der nicht-entropischen Entwicklung einer gesunden Realwirtschaft ist das entwicklungsfähige und souveräne geistig-schöpferische Potential des menschlichen Geistes. Es ist der Input zu diesem Potential, der als Output die effiziente Nicht-Entropie erzeugt.
2. Der entscheidende soziale Teil des Prozesses liegt in dem entsprechenden Potential, das im Individuum angeregt werden muß, um wichtige Entdeckungsakte zu replizieren.
3. Vorbedingung dafür ist die Ausbildung der Individuen und ihrer Beziehungen innerhalb der Gesellschaft, um die Erzeugung und Replikation solcher Ideen zu fördern.
4. Die effiziente Umsetzung dieses sozialen Prozesses hängt davon ab, daß der Mensch die Natur so verändert, daß sie für die erfolgreiche (nicht-entropische) Umsetzung dieser Entdeckungen vorbereitet ist.

Das sind die Axiome, die diese für die Geometrie realwirtschaftlicher Prozesse wesentliche Kausalität bestimmen. Im nicht-entropischen Abbild einer impliziten Mächtigkeitsfunktion bezogen auf die Dichte von Singularitäten pro gewähltem Intervall relevanter Vorgänge spiegeln sich diese Axiome und ihre Implikationen ab. Die Anzahl von Randbedingungen (d. h. Ungleichheiten), die akzeptable Veränderungen der Produktions- und Konsumbeziehungen bestimmen, muß daher mit der Vorstellung einer solchen nicht-entropischen Mächtigkeitsfunktion übereinstimmen: die Anzahl von Ungleichheiten muß in ihrer Wirkung deutlich nicht-entropisch sein.

Wie bereits eingangs bemerkt: Eine mathematische Lösung (im formalen Sinne) wäre wünschenswert, aber eine konzeptionelle Sichtweise ist unabdingbar. Das Wichtigste ist, zu wissen, was zu tun ist. Vor allem muß dies die Überlegung sein, um die Bildungs- und Kulturpolitik zu definieren, die wir zur Entwicklung des geistig-kreativen Potentials des Individuums, insbesondere der Jugend, einsetzen.

Epilog: Das Interaktionsprinzip

Über die Interaktion der beiden axiomatisch inkonsistenten Systeme, des charakteristisch entropischen, linearen monetär-finanziellen Prozesses und des charakteristisch nicht-entropischen realwirtschaftlichen Prozesses, ist folgendes zu sagen.

Es gibt drei typische Zustände, die zu berücksichtigen sind:

1. Beide Prozesse, der monetär-finanzielle Parasit und der realwirtschaftliche Prozeß, sind „symbiotisch“ miteinander verbunden, wobei der Parasit dominiert, jedoch mit der Einschränkung, daß ein Phasensprung des Wirtschaftsprozesses in einen entropischen Zustand nicht stattfindet.
2. Beide Prozesse sind in ähnlicher Weise miteinander verbunden, aber der dominierende monetär-finanzielle Prozeß entkoppelt sich allmählich vom wirtschaftlichen Prozeß; und
3. Der realwirtschaftliche Prozeß wird von der Regierung eingesetzt, um den monetären und finanziellen Prozeß so weit zu steuern, daß letzterer zu einer Nebeninstitution des ersteren wird.

Der erste Zustand ist das, was man als den „normalen“ Symbiosezustand in den industrialisierten Volkswirtschaften während der Jahrhunderte vor 1963 bezeichnen könnte. Der zweite ist der gegenwärtige, völlig degenerierte Zustand der Weltwirtschaft und monetär-finanzieller Systeme. Der dritte ist die bevorzugte Beschaffenheit, wie sie implizit unter der US-Präsidentschaft von George Washington definiert wurde: das sogenannte „Modell“, das vom „Amerikanischen System der politischen Ökonomie“ von Franklin, Hamilton, Carey und List repräsentiert wird.((Siehe u. a. Nancy Spannaus und Christopher White, „The Political Economy of the American Revolution“, Campaigner Publications, New York, 1977.))

Entscheidend bei der Interaktion ist die Rolle einer souveränen nationalstaatlichen Wirtschaftsform. Die „Erfahrung“ im Sinne von Riemanns „Erfahrung“ zeigt uns, daß sich die wünschenswerteste, dritte Form der Interaktion nur durch eine starke Rolle souveräner nationalstaatlicher Regierungen in der Wirtschaft erreichen läßt. Die historische Erfahrung der USA zeigt deutlich, wie diese Regierungsfunktionen in groben Zügen auf mehreren Ebenen aussehen müssen.

Der souveräne Staat muß die Verantwortung für die Kontrolle der Währung und nationaler Kredit-, Währungs- und Finanzangelegenheiten sowie für die Handelsbedingungen behalten. Diese souveräne Autorität muß ganz besonders auf internationale Angelegenheiten angewandt werden, sowie auf einige begrenzte Aspekte des Binnenhandels, wie dies zur wirtschaftlichen Absicherung als notwendig erachtet wird. Die Regierung muß auf den verschiedenen nationalen, regionalen und lokalen Ebenen die Verantwortung für die grundlegende wirtschaftliche Infrastruktur übernehmen, einschließlich Maßnahmen zur Gewährleistung einer vernünftigen Bildung, Gesundheitsversorgung und Förderung des wissenschaftlichen und technischen Fortschritts.((Dazu gehört auch die Wasserwirtschaft, die Instandhaltung der wichtigsten Häfen und Binnenwasserstraßen, Wassereinzugsgebiete und der sanitären Einrichtungen. Auch die allgemeinen öffentlichen Verkehrsmittel sollten entweder in die wirtschaftliche Verantwortung der Regierung oder in den staatlich geregelten Bereich privater Einrichtungen fallen. Die Einrichtung und Regulierung einer geeigneten Stromversorgung für die Regionen und Kommunen ist eine zentrale Aufgabe der Regierung. Auch die grundlegende städtische Infrastruktur fällt in den Zuständigkeitsbereich der Regierung, vor allem der Kommunalverwaltung unter nationaler Führung und staatlicher Regulierung.))

Es ist wünschenswert, daß die meisten verbleibenden Wirtschaftsaktivitäten von bäuerlichen Familienbetrieben und anderen Privatunternehmen wahrgenommen werden. Die dem zugrunde liegenden Wirtschaftsprinzipien finden sich bereits im Frankreich des 15. Jahrhunderts unter Ludwig XI. und allgemeiner in den Nationalstaaten Westeuropas. Beispielhaft für die Ursprünge des modernen Privatunternehmertums ist die Vergabe staatlicher Patente, um Erfindern und ihren Geschäftspartnern zeitlich begrenzte Monopole auf Herstellung und Verkauf zu ermöglichen; daraus ist das zeitlich begrenzte, moderne Patent entstanden, das Erfindern erteilt wird. Die soziale Funktion des Privateigentums besteht darin, die schöpferischen Kräfte, die intellektuelle Besonnenheit und den Mut des einzelnen Unternehmers zu fördern, um methodische und praktische Verbesserungen zum wirtschaftlichen Vorteil der Nation und der Menschheit im allgemeinen hervorzubringen und zu nutzen.

Die Aufteilung von Autorität und Verantwortung zwischen Staat und Privatunternehmer bestimmt sich im wesentlichen durch die Art der sozialen Verantwortung, die jeder von ihnen übernimmt oder vernachlässigt. Die Entwicklung der grundlegenden wirtschaftlichen Infrastruktur stellt die Voraussetzung dafür dar, daß eine Verantwortung für die gesamte Landfläche der betreffenden politischen Einheit, für die Bevölkerung als Ganzes und für jene allgemeinen Angelegenheiten wahrgenommen werden muß, in denen nur der Staat effizient direkte Verantwortung übernehmen kann. Im Rahmen der staatlichen Versorgungs- oder Regulierungsverantwortung sollte der Privatunternehmer über breite, wenn auch begrenzte Befugnisse verfügen.

Das ist keine „gemischte Wirtschaft“, wie einige fehlgeleitete Ideologen es beschreiben würden; es ist der einzige vernünftige Aufbau einer modernen Wirtschaft.

Die größte Leistungsfähigkeit einer Volkswirtschaft wurde durch das erreicht, was im Frankreich von Präsident Charles de Gaulle als „indikative Planung“ bezeichnet wurde. Der Staat setzt seine Monopolstellung zur Regulierung wirtschaftlicher Aktivitäten ein, um die Investitions- und Wachstumsraten bei großen Projekten und anderen besonderen Unternehmensbereichen zu fördern, um so das relativ größte ausgewogenen Wachstum der Wirtschaft insgesamt zu erreichen. Die Verwendung von Staatskrediten zur Förderung nützlicher und notwendiger öffentlicher Bauvorhaben und großangelegter wissenschaftlicher Förderprogramme, wie z. B. Entwicklungsprojekte in der Luft- und Raumfahrt, steht für den strategischen Einsatz öffentlicher Gelder zur Förderung der relativ höchsten langfristigen Wachstums- und Entwicklungsraten in der Wirtschaft insgesamt.

Ein Monopol auf die öffentliche Kreditschöpfung, wie es in Artikel 1 der US-Bundesverfassung vorgesehen ist, und die Konzentration dieser öffentlichen Kredite zur Förderung der Vollbeschäftigung in öffentlichen wie privaten Unternehmen ist das Hauptinstrument, mit dem die Regierung optimale Wachstumsraten von Einkommen, Produktion und Steueraufkommen in der Gesamtwirtschaft fördert.

Es gilt die allgemeine Regel, daß der Staat in der Realwirtschaft relativ hohe Raten der Kapitalintensität, der Energieintensität und des wissenschaftlichen und technischen Fortschritts fördern muß. Dies wird hauptsächlich durch Steueranreize und zinsgünstige öffentliche Kredite erreicht, um die in der Wirtschaftsleistung erzielte „freie Energie“ in innovative produktive Investitionen zu lenken.

Kurz gesagt, das Problem der Wechselwirkung zwischen den beiden grundlegend unterschiedlichen Prozessen ist fast ausschließlich eine Frage der Verantwortung der Regierungen souveräner Volkswirtschaften bei der Regulierung von Währungs- und Finanzangelegenheiten. Das Ziel einer solchen Regulierung muß es sein, die dritte der drei hier genannten möglichen Interaktionsformen herbeizuführen und zu erhalten.

(Deutsche Erstveröffentlichung. Übersetzung: Dr. Wolfgang Lillge)