Erschienen: 1938. Die folgenden zwei Schriften des russischen Naturforschers Wladimir Iwanowitsch Wernadskij (1863–1945) wurden zunächst in englischer Übersetzung und nun auch in deutscher Übersetzung Lyndon LaRouche anläßlich seines 85. Geburtstags am 8. September 2007 gewidmet.

---

Teil I

1. Wir erleben momentan eine Zeit, in der wissenschaftliches Denken im Leben der Menschheit vorherrscht. Im Zusammenhang mit seiner wissenschaftlichen Arbeit wendet sich der Naturforscher heute zwangsläufig einer tieferen, logischen
Analyse der eigentlichen Fundamente seines Wissens zu, die er während des letzten Jahrhunderts ohne weiteres hatte unterlassen können. Die Bedingungen, unter denen er im 20. Jahrhundert arbeitet, nötigen ihn aber gezwungenermaßen dazu; das verlangt seine konkrete, tägliche wissenschaftliche Arbeit und seine Versuchs- oder Beobachtungsmethode.

Die folgenden Umstände, die vom Willen des Naturforschers unabhängig sind, bedingen es.

Zuallererst gibt es darunter ein in der Wissenschaftsgeschichte absolut einmaliges Phänomen, das man derzeit in den Naturwissenschaften – im breitesten Sinn – erlebt und das zu deren radikalen Umbau führt, wodurch dem wissenschaftlichen Denken völlig neue Wege der Untersuchung und des Fortschritts eröffnet werden, welche der Wissenschaft bisher fehlten.

Unter dem Einfluß außergewöhnlich wichtiger, neu aufgedeckter Tatsachen schaffen Wissenschaftler derzeit neue Begriffe, die die Grenzen aller bisherigen Ideen, die Grenzen der kühnsten und fantastischsten Ideen und philosophischen Gedankengebäude weit übersteigen. Zum ersten Mal in der geschriebenen Menschheitsgeschichte entwirft die Wissenschaft mit Hilfe dieser neuen, beispiellosen Methoden nicht bloß spezifische Allgemeinbegriffe, die auf Tatsachen gründen und aus Tatsachen hervorge hen. Darüber hinaus erstellt sie neue Vorstellungen von der Welt, die weit über die spezifischen Tatsachen hinausgehen, diesen aber nicht in der Weise widersprechen, wie die Tatsachen im Widerspruch zu den wissenschaftlichen und philosophischen Begriffen stehen, die unangefochten während des 19. Jahrhunderts herrschten. Diese Begriffe hat die menschliche Kultur über viele Jahrhunderte entwickelt, und sie sind wie vorgefertigt in die Wissenschaft eingegangen. Sie wurden durch die philosophische Forschung über viele Jahrhunderte verfeinert. Gegenwärtig werden sie im Zuge der laufenden wissenschaftlichen Arbeit revidiert und erfahren Veränderungen, die unser Verständnis von ihnen plötzlich umwandeln. Zu diesen Konzepten gehören Zeit, Raum, Energie, Leben, Geometrie usw.

In all dieser entstehenden Bewegung ist die aktive Quelle der Veränderung in den Grundkonzepten nicht Philosophie oder Religion, sondern Wissenschaft. Die wissenschaftliche Arbeit hat diese Konzepte bisher kaum berührt. Sie hat sich in ihnen Platz geschaffen, ohne mit ihnen in Berührung zu kommen, und hat doch ihre Allgemeinbegriffe in sie einfließen lassen.

2. Dieser Zustand des wissenschaftlichen Denkens ging in der Philosophie des 20. Jahrhunderts mit dem Fehlen jeder Kreativität einher, wenn man dies mit dem vergleicht, was so deutlich in der Wissenschaft zum Vorschein kommt. Wissenschaftliche Gedanken beeinflussen derzeit die Philosophie, während die bisherige Ansicht, die Philosophie könne die Realität tiefer ergründen als die Wissenschaft, schwindet.

Die Philosophie lebt heutzutage in der Vergangenheit, und man muß sie im laufenden Umbau des wissenschaftlichen Grundverständnisses der Realität immer weniger berücksichtigen. Die Wissenschaft wird dadurch der Unterstützung beraubt, die die philosophische Analyse wissenschaftlicher Grundkonzepte ihr in den letzten drei Jahrhunderten geboten hat.

Die Grundaussagen der Mathematik werden derzeit eingehend philosophisch analysiert und kritisiert, einschließlich jener der Mechanik und Geometrie sowie in jüngster Zeit auch jener der theoretischen Physik in bezug auf den Atomkern.¹

Doch der gesamte, gewaltige Bereich der biologischen und geologischen Wissenschaft, der eine radikale Umstrukturierung erlebt, bleibt vom philosophischen Denken, welches keine selbständige Analyse der neu aufgedeckten Phänomene geboten hat, im wesentlichen unberührt. In bestimmten Fällen, selbst in neuen Strömungen wie beispielsweise den realistischen Philosophien des Holismus und Organizismus (Whitehead), steht das philosophische Denken eigentlich noch auf dem Boden des 17. Jahrhunderts, denn es hat nicht erkannt, daß es unmöglich ist, „neue Phänomene in alte Weinschläuche zu gießen“. Leider verschließt auch der dialektische Materialismus seine Augen vor diesen neuen Entwicklungen, die nicht in den philosophischen Vorstellungsrahmen der 1840er bis 1880er Jahre passen, in dem er jetzt noch lebt. Mit fortschreitender Zeit, so scheint mir, wird diese Diskrepanz zunehmen, und die Fähigkeit des dialektischen Materialismus, das Beobachtete oder wissenschaftlich Erzeugte zu begreifen, wird abnehmen. Neue, lebendige und schöpferische Arbeit ist erforderlich, um die eigentlichen Fundamente des philosophischen Denkens zu zertrümmern, was derzeit in der schöpferischen Wissenschaftsarbeit geschieht. Kühnes und freies Suchen ist erforderlich. Es muß ein Wechsel von der Interpretation des Alten und der Anpassung des Alten an das Neue hin zu einer kritischen Überprüfung von Grundansichten eintreten.

3. Mir scheint, daß von den neuen allgemeinen Konzepten, die durch die Tatsachen der deskriptiven Naturwissenschaft angeregt wurden, derzeit insbesondere zweien Aufmerksamkeit geschenkt werden sollte: [zuallererst] dem Zustand des Raumes und zweitens der Rechts- und Linkshändigkeit. Sie sind eng miteinander verbunden, doch grundlegend ist der Zustand des Raumes.

Der erste, der darauf in einer grundlegenden Synthese, aber ohne tiefe analytische Abhandlung eingegangen ist, war L. Pasteur nicht lange vor seinem Tod in den 1880er Jahren. Später versuchte Pierre Curie einen tieferen Ansatz, doch meines Wissens ist dieses Konzept nie zum Gegenstand systematischer Überlegungen der Naturforscher oder Philosophen geworden. Der Raum, der empirisch untersucht werden kann, unterscheidet sich vom Raum der Geometrie. Das ergibt sich aus der unzureichenden Tiefe geometrischer Analyse.

Der geometrische Raum ist isotrop; ihm fehlt beispielsweise jede Äußerung von Rechts- und Linkshändigkeit.

Das folgt nicht daraus, wie die Dinge eigentlich sind, sondern ist eine Konsequenz der ungenügend tiefen Analyse der Realität durch geometrische Überlegungen.

Wenn der Naturforscher von Raum spricht, kann er sich die Ergebnisse der Geometrie nur teilweise zunutze machen; bei seinen Beurteilungen geht er mehr und mehr über deren Grenzen hinaus. Das muß bedacht werden. Der geometrische Raum umfaßt derzeit nicht den gesamten empirisch untersuchten Raum – den Helmholtz den physikalischen Raum nannte.

Wenn ich über den Zustand des Raumes spreche, werde ich mich mit dem Zustand des empirischen oder physikalischen Raumes befassen, der nur teilweise von der Geometrie erschlossen wurde. Ihn geometrisch zu begreifen, ist eine Aufgabe für die Zukunft.

Der Zustand des Raumes steht in enger Beziehung mit dem Konzept eines physikalischen Feldes, das in der gegenwärtigen theoretischen Physik eine so bedeutende Rolle spielt. Das Konzept eines Raumzustandes unterscheidet sich vom Konzept eines physikalischen Feldes im wesentlichen dadurch, daß es sich eindeutig in drei Dimensionen äußert; das heißt, es stimmt mit dem geometrischen Raum überein. Aber selbst ein physikalisches Feld ist kein Feld im gewöhnlichen Sinn, da es häufig gekrümmt ist und bei zahlreichen Erscheinungen physikalische Felder besitzt, in denen Kraftlinien verteilt sind – elektrische, magnetische, Wärme-, Gravitations- und elektromagnetische Felder drücken offenkundig einen Teil des geometrischen Raums aus, der sich von diesen scharf abgrenzt. In der Struktur unseres Planeten sehen wir dramatische Äußerungen solcher Felder in großem Maßstab. Dazu zählen die elektrischen oder magnetischen Felder der Erde und das Vakuum der Ionosphäre, die durch zwei Kugelflächen unterschiedlicher Durchmesser begrenzt sind; eine weitere ist das Magnetfeld der Sonne, welches die gesamte Bahn der Erde, ihre Atmosphäre und die Erde selbst umfaßt.

In allen diesen Fällen haben wir es mit Zuständen des Raums zu tun, deren Eigenschaften sich nicht materiell, sondern energetisch äußern. In den Fällen, die Pasteur und Curie gedanklich erfaßt haben, geht es um einem Zustand des Raumes, der sich in erster Linie materiell äußert.

Eigentlich haben wir es schon seit langer Zeit, sogar schon vor Pasteur und Curie, bei jedem Schritt in der Naturwissenschaft mit solchen Fragen zu tun. Pasteur begann von Zuständen des Raums zu sprechen. Helmholtz unterschied den physikalischen Raum vom geometrischen, der eigene Eigenschaften wie Rechts-und Linkshändigkeit besitze. Soweit ich weiß, wurde diese Idee nicht weiterentwickelt.

4. Kristallographen näherten sich seit langem diesem Phänomen. In jedem Kristall, in jedem inerten Naturkörper, äußert sich ein besonderer Aufbau des Raumes. Innerhalb eines Kristalls gibt es ein dreidimensionales physikalisches Feld, dessen Eigenschaften und Zustand durch die Phänomene der Kristallisation hervorgerufen werden. Das ist ein homogener Raum, durchgehend gefüllt mit angestauten Kristallkräften (oder den chemischen Kräften im Festkörperzustand) oder Atompunkten, die ihn vollständig und regelmäßig ausfüllen. Die Verteilung dieser Kräfte läßt sich sehr gut als Sonderfall der Kraftlinien in einem physikalischen Feld verstehen. Im wesentlichen handelt es sich bei homogener kristalliner Substanz – bei Punktsystemen oder Parallelflächnern, die einen gesamten dreidimensionalen Raum einheitlich umfassen, ohne dessen Homogenität zu verletzen – um einen besonderen, anisotropen Raumzustand, der sich streng von dem gewöhnlichen isotropen Zustand des geometrischen Raums unterscheidet. Zahllose Beispiele für solche anderen Zustände des Raums, wie sie in dispergierten² Stoffen zum Ausdruck kommen, sind bekannt und vorstellbar.

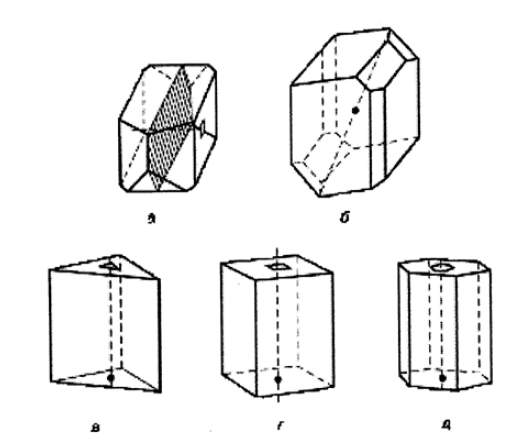
Die Geometrie dieser besonderen Raumzustände ist vollständig durch die Gesetze der dreidimensionalen Euklidischen Geometrie bestimmt. Außerdem läßt sich sagen, daß in diesen räumlichen Punktsystemen, in ihren verbundenen Polyedern – Kristallen –, die Gesetze der Geometrie für uns mit der größten Klarheit hervortreten. A. Poincaré drückte diesen Gedanken sehr deutlich aus, als er beobachtete, daß sich die Geometrie ohne Körper nicht hätte entwickeln können. Bei kristallographischen Phänomenen befinden wir uns vollständig innerhalb der Grenzen der dreidimensionalen Euklidischen Geometrie. Genausowenig verlassen wir ihre Grenzen in physikalischen Feldern wie magnetischen, elektromagnetischen und elektrischen Feldern.

Tatsächlich finden wir in den profunden Konstruktionen von Fjodorow und Schoenflies einen geometrischen Ausdruck der Raumstrukturen, worin die atomare Erscheinungsform des Materieaufbaus eindeutig existieren kann. Dies ist der einzige geometrisch mögliche Ausdruck der atomaren Materiestruktur, die sie klar, eindeutig und genau ausdrückt. In dieser Festkörperstruktur gibt es in ihrer primären Äußerung keine Bewegung von Atomen, so wie diese die gasförmigen und flüssigen Materiezustände auszeichnet. Nimmt man die allgemeine Form dieses Phänomens und berücksichtigt man, daß sich in unserem Raum jegliche chemische Verbindung als Festkörper darstellen läßt, sollten wir in diesen großen, geometrisch ausgedrückten Allgemeinbegriffen von
Fjodorow und Schoenflies eine Gesamteinschließung aller überhaupt möglichen Formen eines in Materie ausgedrückten, anisotropen geometrischen Raumzustands sehen.

5. Aber um die komplexeren Prozesse inerter Naturkörper der Biosphäre aufzuklären, ist es vollkommen möglich (und fruchtbar), einen mehrdimensionalen Raum zu benutzen, um die regelmäßigen Muster auszudrücken, die man beobachtet, wenn man Korrelationen zwischen Materie und ihrer chemischen Zusammensetzung herstellt (wie in den Werken von N. S. Kurnakow und seiner Schule, besonders N. I. Stepanow et al. dargestellt). Aber selbst hier bewegen wir uns nicht außerhalb der Euklidischen Geometrie.

All das sind Phänomene, die mit der Biosphäre oder der Erdkruste in Verbindung stehen.

Es sieht so aus, als wenn das Euklidische Raumverständnis für den geometrischen Ausdruck von Naturerscheinungen im Zusammenhang mit den kosmischen Weiten unzu reichend wäre. Zumindest war man gezwungen, diese Naturerscheinungen betrachten, als man Einsteins theoretische Prämissen analysierte. (Eddington befaßte sich beispielsweise damit – mit einer bestimmten Form des Riemannschen Raums.)

Aber innerhalb der Grenzen der Biosphäre, mit der ich mich hier befasse, müssen wir in ihrer inerten Materie nirgendwo über die Grenzen der Euklidischen Geometrie hinausgehen.

6. Bevor wir fortfahren, muß im Folgenden unterschieden werden, ob wir uns mit materiellen oder mit energetischen Prozessen im Raum befassen. Vom Standpunkt der geometrischen Raumeigenschaften ist es klar, daß sich beide im Raum zwangsläufig unterschiedlich äußern. Geometrie ist keine Äußerung eines apriorischen menschlichen Denkvermögen. Aber aus einer Untersuchung der Geschichte der Geometrie folgt eindeutig – ohne jeden Zweifel, wie mir scheint –, daß sie aus der wissenschaftlichen Erforschung von Erscheinungsformen fester Stoffe in der den Menschen umgebenden Biosphäre erwuchs. Die Übertragung der Gesetze der Biosphäre auf energetische Phänomene war eine Folge davon. Eine solche Übertragung kann diesen Grundaspekt der Geometrie nicht erschüttern.

 

Deshalb sollten wir das geometrische Abbild des festen Materiezustands, wie ihn Schoenflies und Fjodorow in
tiefster und allgemeiner Form aufgezeigt haben, als profundesten Ausdruck der realen dreidimensionalen Euklidischen Geometrie betrachten.

Wissenschaftliche Versuche und Beobachtungen haben gezeigt, daß alle energetischen Äußerungen des festen Materiezustands im Raum die geometrischen Eigenschaften des Raums nicht so umfassend offenbaren wie die atomare Materiestruktur. Hierin drückt sich in der Sprache der heutigen Wissenschaft das sogenannte Neumann-Prinzip aus, benannt nach dem bedeutenden Königsberger Kristallographen, Physiker und Mathematiker [Franz Ernst Neumann].

Entsprechend diesem Prinzip ist weder der flüssige noch der gasförmige Stoffzustand empfindlich genug, um die Raumstruktur in ihrer geometrischen und nicht ihrer dynamischen Erscheinungsform zu erkennen.³ Noch nicht einmal die „schwerelosen Flüssigkeiten“, auf welche die großen Physiker und Philosophen des 17. Jahrhunderts energetische Phänomene reduzierten – vom wissenschaftlichen Standpunkt in einigen Fällen recht zweckmäßig – sind empfindlich genug.

Wie man immer sagt, nehmen Flüssigkeiten und Gase die Form der Gefäße an, die sie enthalten, bleiben also in bezug auf den Raum des Körpers inert. Dies ist ein weiterer Ausdruck für den Vorrang von Festkörpern, um die Geometrie einer Umgebung festzustellen.

Wenn man über den Raum im allgemeinen spricht, müssen wir Neumanns kristallographisches Prinzip erweitern. Geometrisch kann uns nur die Untersuchung materieller Phänomene – metamorph oder kristallin – eine Vorstellung von der Struktur des Raumes geben. Energetische Phänomene oder in Flüssigkeiten oder in Gasen vorkommende Phänomene durchdringen die Geometrie des Raumes weniger tief und können nicht dazu dienen, Licht auf diese Geometrie zu werfen.

Pasteur erkannte dies nicht, als er annahm, daß man mittels Kreisstrahlung oder elektrischem Licht einen für einen lebenden Körper charakteristischen Raum schaffen könnte. Pasteur regte an, ein Experiment zur Urzeugung in einem Medium durchzuführen, das von Strahlen aus kreisförmigem oder elliptisch polarisiertem Licht beleuchtet wird. Dieses Experiment wurde erst nach Pasteurs Tod ausgeführt. Es offenbart die Wirkung dieser Strahlen auf lebende Phänomene, aber in Übereinstimmung mit Neumanns Prinzip verändert es in keiner Weise die Struktur des Raumes.

Die folgenden Ausführungen gründen sich auf diese geometrische Natur materieller und energetischer Phänomene im geometrischen Raum. Materielle Phänomene liefern eine grundlegendere Vorstellung der geometrischen Raumstruktur als energetische.

7. Jetzt richten wir unser Augenmerk auf Phänomene der Rechts- und Linkshändigkeit, soweit sie sich auf die Symmetriegesetze beziehen.

Wie wir gesehen haben, sind Rechts-und Linkshändigkeit im dreidimensionalen Euklidischen Raum, was die materiellen Prozesse betrifft, geometrisch und physikalisch äquivalent. Diese Äquivalenz zeigt sich in der Tatsache, daß die Anzahl der kristallographisch rechten und linken Polyeder, die bei der Kristallisation gebildet werden, identisch ist (bei Abwesenheit lebender Organismen im Medium). Diese Zahl entspricht den Gesetzen der Wahrscheinlichkeitstheorie. Bei einer genügenden Anzahl ist das Mengenverhältnis zwischen rechten und linken Polyedern gleich eins. Je höher die Anzahl, desto mehr nähert sie sich der eins an.

Die Beobachtungen, die Lemmleyn in unserem biogeochemischen Labor mit Quarzen angestellt hat, und die noch größeren Fallzahlen von Trommsdorf in Göttingen bestätigen dies vollkommen.

Pasteurs große Entdeckung zeigte, daß dies bei Kristallisationsphänomen in lebenden Organismen oder, noch tiefreichender, während der biochemischen Bildung rechter und linker Moleküle in lebenden Organismen nie auftritt.

Pasteurs Idee einer Verbindung zwischen diesem Phänomen und dem geometrischen Raum lebender Organismen erkenne ich als geniale Eingebung voll an. Aber da er nicht zwischen den materiellen und energetischen Eigenschaften des Raumes unterschied, vermutete Pasteur irrtümlich, daß das Leben auf unserem Planeten in einer vergangenen geologischen Geschichtsperiode entstanden sei, als das Sonnensystem linksdrehenden kosmischen Raum durchquerte. Er vermutete weiterhin, daß linksdrehende und rechtsdrehende Räume im kosmischen Raum getrennt seien. Wie wir am dreidimensionalen Euklidischen Raum und am Euklidischen Raum im allgemeinen sehen, kann dies in bezug auf Materie nicht der Fall sein. Energetische Äußerungen im Raum geben uns dazu keine Beurteilungsmöglichkeit. Die Unterteilung in rechts und links, wie sie dem Leben entspricht, d. h. die Ungleichheiten von Rechts- und Linkshändigkeit, dürfen nicht in den energetischen, sondern müssen in den materiellen Eigenschaften des Raums festgemacht werden.

8. Die geometrischen Symmetriegesetze wurden für die Euklidische Geometrie aufgestellt, und sie wurden in bezug auf den Raum in endgültiger Form Ende letzten Jahrhunderts von Je.S. Fjodorow in St. Petersburg und A. Schoenflies in Göttingen ausgedrückt. Sie hatten viele Vorgänger, wie zum Beispiel Frankenhelm, Bravais und Sohnke, aber sie haben das Problem als erste endgültig gelöst: Schoenflies mit Hilfe der Gruppentheorie und Fjodorow geometrisch, indem er den Raum gleichförmig, ohne leere Zwischenräume mittels Paralleloeder stetig verschob. Der Kristallpolyeder wurde aufgegeben und geometrisch durch ein Punktsystem an den Spitzen von Paralleloedern ersetzt, die gesetzmäßig, aber nicht gleichförmig im unbegrenzten Raum der dreidimensionalen Euklidischen Geometrie lagen.

Bald darauf war Paul von Groth in München der erste, der darauf hinwies, daß es sich logisch aus dem Werk Fjodorows ergebe, daß Kristalle in ihrer inneren Struktur nicht durch Moleküle, wie die Kristallographen dachten, sondern durch Atome gekennzeichnet sind. Zuvor war dies von Gaudin in der erste Hälfte des 19. Jahrhunderts klar verstanden worden. Die Entdeckung der Röntgen-Kristallographie 1911 durch M. von Laue, Knipping und Friedrich in München in Zusammenarbeit mit Groth lieferte den endgültigen Beweis.

Daraus müssen wir schließen, daß der atomare Zustand von Festkörpern im physikalischen Raum zwangsläufig, erstens, die Untrennbarkeit von Rechts- und Linkshändigkeit und, zweitens, ihre physikalische und folglich chemische Äquivalenz verlangt. Die Existenz von Atomen im physikalischen Raum ist für uns eine unbestreitbare Tatsache, auf der unsere gesamte wissenschaftliche Vorstellung der Realität beruht. In einem festen Medium kann es keinen Unterschied zwischen Rechts-und Linkshändigkeit geben; außerdem sind die Unterschiede im Zusammenhang mit Vektoren „in Richtung der Sonne“ und „entgegen der Sonne“ in jeder anderen Hinsicht identisch. Dies ist eine zwangsläufige logische Folge der Atomstruktur der Materie und der dreidimensionalen Euklidischen Geometrie.

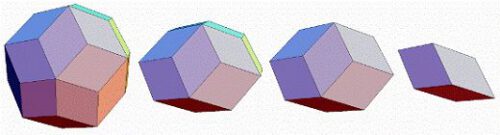
9. Diese Schlußfolgerung erfordert weitere Betrachtung. Es ist noch einmal nützlich, sich zu vergegenwärtigen, daß wir es hier nicht nur mit den Eigenschaften von Kristallen, sondern mit der Verteilung von Atomen in Raumgittern zu tun haben. Daraus folgt geometrisch, daß bestimmte Symmetrieelemente in atomaren Prozessen nicht darstellbar sind. Die ersten Kristallographen haben bereits darauf verwiesen, daß von den fünf regelmäßigen pythagoräischen Polyedern der regelmäßige Dodekaeder nicht unter den Kristallen anzutreffen ist, und vor einem Jahrhundert bewies Bravais, daß entsprechend die Symmetrieachse fünfter Ordnung, die den Dodekaeder kennzeichnet, nicht auftreten kann, denn wenn sie zulässig wäre, müßte das Gesetz der rationalen Indizes, das für Kristalle empirisch aufgestellt wurde, als inkorrekt erkannt werden. Dies drückt sich deutlich in dem Umstand aus, daß ein aus Atomen bestehender Körper, der eine solche Symmetrieachse fünfter Ordnung besitzt, nicht die Möglichkeit einer beliebigen endlichen Entfernung zwischen zwei Atompunkten erlaubt. Sie werden sich einander stets auf eine Entfernung annähern, die kleiner als die gegebene Entfernung ist. Physikalisch hätten wir es hier mit einem stetigen, nicht-dispergierten Festkörperzustand zu tun. Gleichzeitig läßt sich ein regelmäßiger Dodekaeder aus jedem festen Material einfach erhalten oder herstellen. Aber aus dieser gleichen Grundannahme, aus der Festkörperstruktur, aus der homogenen räumlichen Verteilung von Atomen mit festen endlichen Dimensionen (oder mit Kräften, die
nicht zulassen, daß der Einfluß des Radius eines anderen Atoms in ihre Region eindringt) – aus all dem folgt auf der gleichen Grundlage, daß die Zahl der in Kristallkörpern vorkommenden Symmetrieelemente streng begrenzt ist. Keine Symmetrieachse größer als sechs ist in ihnen möglich und wird auch nicht beobachtet. Von der unzähligen Menge regelmäßiger Polyeder in der Geometrie werden nur relativ wenige in Naturkörpern angetroffen, und diese bestehen aus homogen und regelmäßig verteilten Atomen im dreidimensionalen Euklidischen Raum.

10. Darin äußert sich nicht nur die Atomstruktur der Materie, sondern auch der dreidimensionale Euklidische Raum, in dem sich die Körper befinden.

Von diesem Standpunkt wird es grundlegend bedeutsam, daß in diesem Raum eine solche Verteilung der Atome immer möglich ist, aber dann werden zwangsläufig zwei physikalisch identische Abarten spiralig gewundener Verteilungen von Atomen gebildet – rechte und linke. Diese spiralig gewundenen Atomverteilungen sollten sich zwangsläufig in Kristallstrukturen äußern, wenn komplexe Symmetrieelemente wie ein Symmetriezentrum, Symmetrieebenen oder eine vierfache komplexe Symmetrieachse fehlen. Bei der natürlichen Kristallisation ist die Menge solcher unterschiedlich ausgerichteter gewundener Spiralatome stets identisch und von zufälliger Ursache bestimmt.

Die von Pasteur entdeckte Verletzung dieses Prinzips in lebenden Naturkörpern läßt die Frage aufkommen, was die Ursache dieses Phänomens sein könnte.

Sie kann natürlich nicht der Atomstruktur der Materie widersprechen, die sich so scharf und eindeutig in lebenden Naturkörpern ausdrückt, worin sich atomare Eigenschaften vielleicht noch grundlegender zeigen als in inerten Naturkörpern.

Die Ursache könnte entweder in besonderen Symmetrieformen lebender Organismen oder in besonderen Eigenschaften des von Körpern lebender Materie besetzten Raumes liegen.

Dies sind die theoretisch möglichen Prämissen, die mit dem Konzept lebender Materie als Gesamtheit lebender Organismen tatsächlich verbunden sind. Damit vermeide ich das glatte Terrain der „Lebens“-Eigenschaften. In der Realität, in der Biosphäre, untersuchen wir genau auf diese Weise die Phänomene und Äußerungen des Lebens – lediglich als „lebende Materie“.

11. Bevor wir fortfahren, sollten wir innehalten und das Phänomen der Symmetrie in bezug auf den lebenden Organismus betrachten. Das eigentliche Konzept von Symmetrie nahm im Zuge der Beschäftigung mit lebenden Organismen Gestalt an. Wie es überliefert ist, schuf Pythagoras von Rhegium mehrere Jahrhunderte v.Chr. das Konzept und das Wort „Symmetrie“, um die Schönheit des menschlichen Körpers und Schönheit im allgemeinen auszudrücken. Darin fanden bereits die alten Griechen gesetzmäßige Zahlenmuster, die jedoch in der Folge bis auf den heutigen Tag kein Verständnis eines mathematischen Allgemeinbegriffs erbracht haben. Als Bravais sich in der ersten Hälfte des 19. Jahrhunderts mit dem Konzept der Symmetrie beschäftigte, betrachtete er gleichzeitig die Symmetrie von Kristallen und die Symmetrie lebender Organismen. Er erzielte brillante Ergebnisse für Kristalle, womit er das Fach der Kristallsymmetrie begründete, das am Ende des Jahrhunderts zu einem gut ausgebildeten System atomarer Raumpunkte und zur vollständigen Beschreibung ihrer Geometrie führte.

Eine Krankheit unterbrach seine Arbeit über die Symmetrie lebender Organismen. Niemand danach untersuchte diese so tiefgehend wie Bravais, und sie ist bis zur heutigen Zeit in einem Zustand des Chaos verblieben.

Es ist jedoch deutlich sichtbar, daß es zwischen der Symmetrie von Kristallpolyedern und der Symmetrie lebender Organismen einen grundlegenden, tiefen Unterschied gibt. Im ersten Fall haben wir es mit dem Ausdruck der Atomstruktur eines Festkörpers zu tun, während es beim zweiten um ein Streben nach Ordnung seitens der lebenden Materie geht, die isoliert und abgetrennt innerhalb der fremden, inerten Umgebung der Biosphäre existiert.

Symmetrie drückt sich hier in der äußeren Form jenes ewig beweglichen, dispergierten Elements lebender Materie – eines großen oder unbedeutend kleinen lebenden Organismus – aus, das durch die biogene Wanderung von Atomen geschaffen und erhalten wird und sich als Körper äußert, der sich von der ihn umgebenden Natur deutlich unterscheidet. Die Symmetrie drückt sich auch in seiner inneren Struktur, seiner Organisation und seinem makroskopischen und mikroskopischen Querschnitt aus.

12. Die Gesetze dieser Symmetrie sind uns völlig unbekannt. Aber ihre Existenz, die Existenz morphologischer Regelmäßigkeit, steht außer Zweifel. Es ist klar, daß diese Symmetrie ganz anderen Gesetzen folgt als jene, welchen die Kristallsymmetrie folgt.

Geometrisch fallen unmittelbar zwei Phänomene auf. Zuallererst weisen lebende Organismen Symmetrieachsen fünfter oder höher als sechster Ordnung auf. Dies deutet darauf hin, daß wir es hier nicht mit der Symmetrie oder der Atomstruktur eines homogenen Festkörpers zu tun haben. Die Homogenität der inneren Struktur, die für Kristalle so kennzeichnend ist, fehlt hier. Das Innere eines lebenden Organismus ist überaus heterogen, seine Atome befinden sich in ständiger Bewegung und kehren nie an die gleichen Stellen zurück, an denen sie einmal waren; ganz anders als bei Kristallen, worin sich die Atome Milliarden Jahre lang nicht verschieben, wenn nicht äußere Kräfte dies bewirken. [Zweitens,] innerhalb eines lebenden Organismus haben wir es mit einer ständigen Abfolge dynamischer, stabiler Gleichgewichte zu tun, die durch die biogene Wanderung von Atomen gesteuert werden. Bei der Symmetrie eines lebenden Organismus müssen wir somit ein neues Element, die Bewegung, betrachten, die bei der Kristallsymmetrie fehlt, weil sich die Atome in Kristallen nicht verschieben und diese somit idealerweise einen Festkörper darstellen. Es ist kennzeichnend, daß die biogene Wanderung von Atomen, welche die dynamische Gleichgewichtsform eines lebenden Organismus erzeugt,

in einem flüssigen oder gasförmigen Medium erfolgt – in
jenem Medium, welches das am wenigsten ausgeprägte ist, um die Geometrie des Raumes auszudrücken, den der Körper lebender Materie einnimmt.

Schließlich sollte hier ein dritter, extrem typischer Aspekt hervorgehoben werden, einer, der in Kristallen fehlt, der aber ein Hauptelement in der morphologischen Form eines lebenden Organismus ist. In der Morphologie lebender Organismen herrschen gekrümmte Linien und gekrümmte Flächen als primäre Äußerungen ihrer Symmetrie vor. In Kristallpolyedern, im wesentlich in den „Tröpfchen“, die kristallinen Raumgittern entsprechen, sind gekrümmte Flächen und gekrümmte Ebenen sekundäre Phänomene. Sie sind mit der Wirkung von Oberflächenkräften während der Kristallisation und in Äußerungen (von Kräften) im Flüssigkeitsraum verbunden. Dazu gehören Auflösungserscheinungen und verwandte Auflösungsflächen von Kristallen. Diese gekrümmten Flächen sind bei sämtlichen energetischen Eigenschaften von Kristallen noch ausgeprägter, wo der Polyeder verschwindet und durch eine Kugel, ein Hyperboloid, ein Ellipsoid usw. ersetzt wird. Dies sind Fälle, wo Neumanns Prinzip besagt, daß sich die geometrische Raumstruktur in diesen Phänomen am wenigsten widerspiegelt.

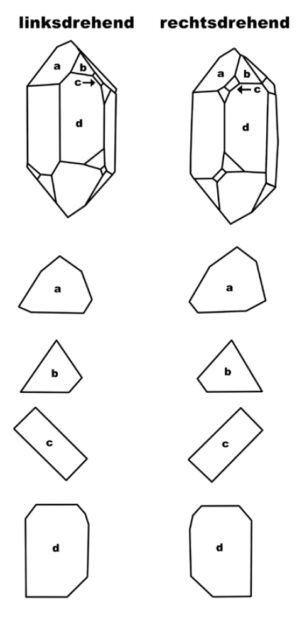
13. In der Symmetrie lebender Organismen sind Rechts-und Linkshändigkeit extrem ausgeprägt, während sie bei Kristallen ein Sonderfall sind, deren Auftreten mit dem Fehlen komplexer Symmetrie verbunden ist.

Aber, wie ich bereits erwähnt habe, gibt es in bezug auf die Symmetrie einen grundlegenden Unterschied zwischen dem Auftreten von Rechts- und Linkshändigkeit in Organismen und ihrem Auftreten in Kristallen. Dieser Unterschied besteht in der physikalisch-chemischen Äquivalenz von Rechts-und Linkshändigkeit in Kristallen, welche sich dadurch äußert, daß während der Kristallisation rechte und linke Formen in gleicher Anzahl auftreten. Dies geschieht immer und könnte, wie ich in Abschnitt 8 erwähnte, als Äußerung der atomaren Festkörperstruktur im dreidimensionalen Euklidischen Raum angesehen werden. Dies ist ebensosehr eine Eigenschaft der Symmetrie wie eine Eigenschaft des dreidimensionalen Euklidischen Raums.

Etwas vollkommen anderes beobachten wir in lebender Materie.

Hier tritt die Ungleichheit von Rechts-und Linkshändigkeit unmittelbar in Erscheinung. Es gibt eine enorme Fülle von Material, das noch nicht kritisch durchgearbeitet wurde, aber mir scheint, es läßt sich auf Grundlage dieses Materials einwandfrei feststellen, daß in Organismen – in lebender Materie – diese Ungleichheit bei einer ganzen Reihe unterschiedlicher Eigenschaften extrem ausgeprägt ist. Sie wird weitervererbt und ist ein Gattungskennzei chen. Alle Eiweiße in Tieren wie in Pflanzen zeigen eine Linksdrehung der Lichtebene. Das bedeutet, daß in der komplexen Materie lebender Körper nur linke Isomere von Eiweißkörpern – dem Hauptbestandteil des Protoplasmas – stabil sind. Rechte Isomere fehlen. Wie Pasteur zeigte, sind alle kristallinen Verbindungen – Alkaloide, Glukosen, Zucker usw., woraus Eier oder Getreide bestehen, d. h. für das Leben am essentiellsten sind – linkshändig. Diese letzte Behauptung erforderte eine genauere Besprechung, auf die ich in diesem kurzen Aufsatz nicht eingehen kann. Aber im allgemeinen scheint sie mir zu stimmen, und manchmal dürften Schwierigkeiten nur deswegen entstehen, weil die komplexen organischen Verbindungen in Körpern lebender Materie gleichzeitig linke und rechte Komplexe als ihre Bestandteile haben. Dieser Umstand erfordert einen Nachweis, angefangen mit der kritischen Bearbeitung sämtlichen Materials.

Nicht weniger ausgeprägt ist der chemische Wirkunterschied von rechten und linken Isomeren auf das Zellprotoplasma.

Eine Reihe präziser Experimente auf diesem Gebiet, die von G. F. Gause teilweise in Zusammenhang mit der Arbeit unseres Labors entworfen wurden, hat dies kürzlich über jeden Zweifel bewiesen. In identischem Aufbau und unter identischen Bedingungen wirken hier rechte und linke chemische Verbindungen in dem komplexen thermodynamischen Umfeld lebender Materie als Körper, die chemisch überaus unterschiedlich sind. Sie deuten auf eine eigenartige geometrische Struktur hin, die sich im lebenden Organismus und besonders in einer Zelle für rechte und linke [Isomere] dynamisch unterschiedlich darstellt.

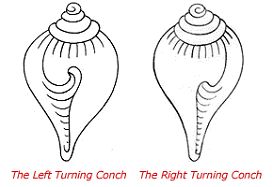
Die Ungleichheit von Rechts- und Linkshändigkeit drückt sich nicht nur in ihren chemischen und physikalischen Erscheinungen aus. Sie umfaßt die gesamte Morphologie des Organismus und darüber hinaus seine Dynamik. Besonders kennzeichnend ist die Bedeutung von Spiralen bei der Form von Organismen sowie die Ungleichheit rechter und linker Spiralen. Dies drückt sich in der Ungleichheit rechter und linker Windungen bei Muscheln, Bakterien, Samen, Pflanzenranken usw. aus. Man sieht sie im seltenen Auftreten von „Linkshändigkeit“, obgleich bei bestimmten Organismen „Linke“ vorherrschen und als Gattungskennzeichen gelten können.

Ich lasse die zahlreichen und verschiedenartigen Erklärungen dieses allgemeinen Phänomens völlig beiseite. Sie sind von Fall zu Fall formuliert, und im allgemeinen scheinen sie mir nichts zu erklären.

Teil II

 

1. Der Zustand des Raumes ist eng mit der Vorstellung eines physikalischen Feldes verbunden, unterscheidet sich aber von letzterem darin, daß er sich eindeutig in drei Dimensionen darstellt. Aber auch ein physikalisches Feld, beispielsweise ein elektromagnetisches Feld, hat in Wirklichkeit eine Krümmung, und Phänomene darin spielen sich nicht auf einer Fläche ab. In der Ionosphäre haben wir einen sehr ausgeprägten, besonderen Raumzustand dieser Erdhülle, ein besonderes physikalisches Feld – das Feld eines physikalischen Vakuums in Form eines dreidimensionalen Raumes, der von Kugelflächen unterschiedlicher Radien begrenzt ist.

In der Realität stoßen wir sogar bei jedem Schritt auf unterschiedliche Raumzustände. So gibt es innerhalb eines Kristalls ein dreidimensionales physikalisches Feld, dessen Eigenschaften durch die Phänomene der Kristallisation festgelegt sind. Es ist ein homogener Raum, durchgehend gefüllt mit angestauten Kristallkräften (den chemischen Kräften der Materie im Festkörperzustand), mit Atompunkten, die ihn vollständig und regelmäßig ausfüllen. In homogener Kristallsubstanz – in Punktsystemen oder Parallelflächnern, die einen gesamten dreidimensionalen Raum einheitlich umschließen, ohne dessen Homogenität zu verletzen – haben wir im wesentlichen den Fall eines besonderen anisotropen Raumzustands, der sich scharf von dem gewöhnlichen isotropen Zustand des geometrischen Raums unterscheidet. Geometrisch lassen sich Hunderte solcher unterschiedlicher Raumzustände unterscheiden, wie sie sich auf verschiedene Weise in dispergierter Materie ausdrücken. Aber die Geometrie dieser besonderen Raumzustände ist vollständig durch die Gesetze der Euklidischen Geometrie bestimmt. Genausowenig verlassen wir in magnetischen, elektrischen und elektromagnetischen Feldern die Grenzen der Euklidischen Geometrie und befinden uns weiterhin im dreidimensionalen Raum.

Aber bei komplexeren Phänomenen ist es zweckmäßig und möglich, in der Euklidischen Geometrie geometrische Darstellungen mehrdimensionaler Räume zu verwenden.⁴

Man kann sagen, daß wir bei allen diesen Phänomenen nie die Grenzen inerter Naturkörper der Biosphäre überschreiten. In diesem Bereich der Erscheinungen befinden wir uns vollständig innerhalb Euklidischer Geometrien. Diese Euklidischen Geometrien drücken sich in den anisotropen Räumen der Kristallographie in dreidimensionaler Geometrie aus, während sie sich in der Korrelation von chemischen Eigenschaften und Materie bei den Konzepten Kurnakows in dreidimensionalen, vierdimensionalen, fünfdimensionalen und höheren komplexen Geometrien ausdrücken.

Man könnte nun meinen, daß wir nirgendwo innerhalb der Grenzen inerter Naturkörper und der Phänomene der Biosphäre den Bereich der Euklidischen Geometrie verlassen. Wir gehen nur solange nicht darüber hinaus, bis wir auf planetare Phänomene stoßen.

Diese Konzepte reichen offenbar nicht aus, wenn wir die Grenzen unserer planetaren Welt überschreiten und in den kosmischen Raum eintreten.

Aber diese Phänomene, die mit Einsteins Ideen zusammenhängen, liegen außerhalb meines Blickfeldes, insoweit ich mich mit den inerten und lebenden Naturkörpern der Biosphäre beschäftige, die eine kleine Hülle unseres Planeten ist.

2. Doch sobald wir uns mit lebenden Naturkörpern beschäftigen, stoßen wir auf eine grundlegende Änderung in den geometrischen Phänomenen, welche mir nicht in die Abgrenzungen der Euklidischen Geometrie jeglicher Dimensionen zu passen scheint.

Grundlegend ist hier die deutliche Verletzung, erstens, der Symmetrie und, zweitens, die Erscheinungsformen von Rechts- und Linkshändigkeit.

Die Symmetriegesetze wurden für die Euklidische Geometrie nur geometrisch aufgestellt, während sie in der Gruppentheorie nicht nur geometrisch, sondern auch algebraisch ausgedrückt wurden, und auf diesen zwei unabhängigen logischen Wegen erzielte man die gleichen Ergebnisse. Geometrisch ergaben sie sich aus der Verteilung der Punkte im Raum, wo diese Punkte immer einen bestimmten Parameter, einen bestimmten Abstand hatten, unterhalb dessen sie sich nicht weiter annähern konnten. Bei den uns umgebenden Phänomenen, die sich auf Punkte reduzieren lassen, d. h. auf Atome, aus denen die Materie aufgebaut ist, stoßen wir nirgends auf eine Verletzung der Symmetriegesetze.

Diese Gesetze werden innerhalb der Grenzen des von lebender Materie eingenommenen Raums verletzt, wobei ich unter „lebender Materie“ die Gesamtheit aller lebenden Organismen verstehe. Der Verstoß kommt äußerst anschaulich dadurch zum Ausdruck, daß sich rechts- und linkshändige Kristallgitter (mit rechts- und linkshändiger innerer Atomstruktur) im Innern lebender Organismen sehr unterschiedlich für ein und dieselbe chemische Verbindung ausdrücken, die sich dann aber chemisch als sehr unterschiedlich erweisen.

3. Leider sind diese Symmetriephänomene und die Phänomene der Rechts- und Linkshändigkeit – erstere umfassen sämtliche geometrischen und physikalischen Grundmuster von Feststoffen, und letztere kennzeichnen die Körper lebender Organismen – lange Zeit außerhalb des Blickfeldes der Mathematiker und Philosophen geblieben und sind es teilweise immer noch.

Man könnte sagen, die philosophische Analyse fehlt. Aber die mathematische Analyse (geometrisch wie algebraisch) dispergierter regelmäßiger Systeme von gleichbleibenden Parametern von Atompunkten erfolgte brillant, man könnte sagen endgültig, in der Arbeit von Je.S. Fjo dorow in St. Petersburg und A. Schoenflies in Göttingen am Ende des 19. Jahrhunderts. Im Verlauf dieser Arbeit wurde übrigens festgestellt, daß in den inerten Naturkörpern unseres Planeten bei weitem nicht alle geometrisch vorstellbaren Polyeder angetroffen werden können. Insbesondere beobachtet man einen der fünf pythagoräischen Körper, den regelmäßigen Dodekaeder, nicht unter den inerten Naturkörpern der Erdkruste. Dies ist eine Folge der dispergierten Struktur fester chemischer Verbindungen: sie bestehen aus Atomen, die sich einander nie auf einen Abstand unter einer bestimmten Größe annähern können, welche bei jedem Isotop anders ist. Eine weitere geometrische Folge dieses gleichen Grundphänomens ist, daß in den geometrischen Materiestrukturen – in Kristallen und Molekülen – Rotationssymmetrieachsen fünfter, siebenter und höherer Ordnung nicht vorkommen können.

Das Phänomen der Symmetrie, das durch die Mathematik nur teilweise verstanden wurde, gelangte in die Wissenschaft in Zusammenhang mit dem Schönheitsemp finden, das sich in der Menschheit vor vielen Tausenden Jahren entwickelte. Dieses Konzept entsprang der hellenistischen Denkart im ersten Jahrtausend v. Chr. In der Überlieferung hat sich der Name des Pythagoras von Rhegium erhalten, der es als erster benannte. Aber den Weg in die Wissenschaft fand das Konzept von Symmetrie im 17. Jahrhundert und in allgemeinerer Form im 18. und 19. Jahrhundert. Es hat zwei Wurzeln. Einerseits entsprang es der Beobachtung inerter Naturkörper der Biosphäre – Schneeflocken und Kristallen – und andererseits aus der Beobachtung lebender Organismen hauptsächlich durch Bravais Mitte des 19. Jahrhunderts. Bravais, der sich dem Studium der Kristalle vom Standpunkt seines primären wissenschaftlichen Interesses an der Biologie widmete, legte die Grundlage für die geometrische Untersuchung der Kristallsymmetrie und stellte gleichzeitig die ganz anderen Symmetrieeigenschaften von Lebewesen im Vergleich zu den Kristallen dar. Doch seine Arbeit, die Arbeit eines profunden Geometers und Naturforschers, wurde im besten Alter von einer unheilbaren Krankheit unterbrochen. Der Faden, den er fallen ließ, wurde von niemandem aufgenommen. Was die Geometrie angeht, so befindet sich die Symmetrie lebender Organismen in einem chaotischen Zustand. Die zusammengetragenen Fakten wurden von der Geometrie nicht erfaßt. Mir scheint, niemand ist über Bravais hinausgegangen.

Erstaunlicherweise ist das Konzept von Symmetrie außerhalb der Reichweite philosophischer Überlegungen geblieben, und mir scheint, seine Bedeutung ist in der Wissenschaft nicht ausreichend tief betrachtet worden, obgleich seine Bedeutung vielen klar ist und obgleich sich daraus die offensichtliche Möglichkeit weiterer mathematischer Untersuchungen ergeben.

4. Noch schlimmer ist es um den Begriff der Rechts- und Linkshändigkeit bestellt, dessen enorme Bedeutung und sehr unterschiedliche Erscheinungsweise in lebenden und in inerten Naturkörpern von Louis Pasteur sehr klar Mitte des letzten Jahrhunderts herausgearbeitet wurden. Eigentlich ist niemand tiefer als er vorgedrungen. Die Geometer haben dieses Konzept ignoriert. Die Kristallographen haben festgestellt, daß es sich in den rechts- und linkshändigen Helixspiralen ausdrückt, in denen die Isotope in Kristallstrukturen verteilt sind. Pasteur hatte als erster nachgewiesen, daß das gleiche Phänomen in bestimmten chemischen Verbindungen – in Molekülen – beobachtet werden müsse. Aus seinen Beobachtungen zog er den richtigen Schluß, daß es einen deutlichen Unterschied darin gibt, wie sich diese Phänomene in lebenden und in inerten Naturkörpern ausdrücken. Die auf Grundlage von Kristallstudien abgeleiteten Symmetriegesetze werden in lebenden Naturkörpern einschneidend verletzt.

Pasteur verstand, wie Bechamps etwas vor ihm, die Bedeutung der Rechts-und Linkshändigkeit aufgrund der Beobachtungen von Technikern im Elsaß, die durch die Einwirkung lebender Schimmelpilze auf racemische Säure und ihre Salze linksdrehende Weinsäure und ihre Salze erhalten hatten. Höchstwahrscheinlich hatte Pasteur recht (leider ist dies noch nicht schlüssig bestätigt), daß entgegen den Symmetriegesetzen alle für das Leben notwendigen Hauptbestandteile im kristallisierten Zustand (Verbindungen, die Bestandteile von Samen, Eiern, Sporen usw. sind) nur in Form linker Isomere beobachtet werden. Nichtkristalline – kolloidale oder mesomorphe – Eiweiße sind immer linkshändig. Bisher hat man rechtshändige Isomere von Eiweißen und die kristallinen Hauptproduk te ihres Abbaus nur im Labor erhalten. Im Pflanzen- und Tierreich beobachtet man nur die linken Isomere.

Dies drückt sich in der besonderen Eigenschaft lebender Organismen aus, nämlich sich von rechten Isomeren zu ernähren und diese in ihrem Körper umzuwandeln. Nur linke Isomere gehen in den Aufbau eines lebenden Körpers ein. Diese Erklärung ist eine einfache Aussage und kann eigentlich nicht als eine Erklärung gelten. Sie ist für uns genauso unbegreiflich wie die Tatsache selbst.

5. Da Rechts- und Linkshändigkeit von Kristallkörpern im dreidimensionalen Euklidischen Raum chemisch identisch sind, entsteht zwangsläufig die Frage, ob diese von Bechamps und Pasteur verstandene (und zuvor
von Bechamps unabhängig experimentell bewiesene) Tatsache dadurch erklärt werden könne, daß lebende
Organismen eine besondere, noch nicht verstandene Eigenschaft besitzen, mittels derer sie gegen die Äquivalenz von Rechts- und Linkshändigkeit verstoßen und ihre Körper aus linken Isomeren der für das Leben notwendigen Grundmolekülen aufbauen. Ist das nicht eine Tautologie? Und wäre es nicht richtiger, sich wie Pasteur den Eigenschaften des Raumes zu widmen, in dem das Leben stattfindet und worin es entstand?

Sicherlich ist es so, daß Rechts- und Linkshändigkeit im Euklidischen Raum zweifellos eine geometrische Eigenschaft dieses Raumes sind. Das ergibt sich aus den seit langem bekannten geometrischen Erkenntnissen, daß Rechts- und Linkshändigkeit in der vierten Dimension des Euklidischen Raums nicht in Erscheinung treten. Bereits Kant hat dieses Phänomen untersucht, und er betonte, daß rechte und linke Hände im vierdimensionalen Euklidischen Raum zusammenfallen. Es ist klar, daß diese Eigenschaft – Rechts- und Linkshändigkeit – Kennzeichen Euklidischer Räume ungeradzahliger Dimensionalität ist.

Aus den oben erwähnten Symmetrieeigenschaften ist deutlich, daß es sich hierbei nicht nur um eine physikalisch-chemische Eigenschaft handelt, da die Äquivalenz von Rechts-und Linkshändigkeit in all ihren Erscheinungsformen, ob diese geometrisch oder physikalisch-chemisch sein mögen, für ein homogenes Punktsystem beobachtet wird, das den gesamten dreidimensionalen Euklidischen Raum kontinuierlich ausfüllt. Das ergibt sich zwangsläufig aus den Konstruktionen von Schoenflies und Fjodorow. Pasteur wußte das nicht. Aber mit der Intuition des Genies verstand er die Tiefe des Phänomens, mit dem er es zu tun hatte. Und er suchte in den Eigenschaften des kosmischen Raums nach einem Ausweg. Er vermutete, daß das Sonnensystem in einer vergangenen geologischen Geschichtsperiode linken kosmischen Raum durchquert hätte, in der damals Leben entstanden sei und dieses Phänomen darin zum Ausdruck komme. Doch Pasteur kannte die geometrischen Folgen nicht, die sich aus der Ar beit von Schoenflies und Fjodorow ergeben – die geometrische Äquivalenz von Rechts-und Linkshändigkeit im dreidimensionalen Euklidischen Raum – und die sich geometrisch in Raumgittern von Atompunkten ausdrücken. Daraus folgt, daß die Äquivalenz von Rechts-und Linkshändigkeit als geometrische Eigenschaft des dreidimensionalen Euklidischen Raums betrachtet werden kann.

6. Um die Ungleichheit von Rechts- und Linkshändigkeit und das markante Auftreten linkshändiger chemischer Verbindungen innerhalb der Körper von Lebewesen zu erklären, sind wir gezwungen anzunehmen, daß wir es entweder in diesem Fall nicht mit einem Euklidischen Raum zu tun haben, oder daß Organismen eine besondere Fähigkeit besitzen, die rechten Isomere beim Aufbau ihrer Körper zu benutzen,⁵ während linke Isomere in den Körpern lebender Organismen abgelagert werden.

Bevor man die Existenz eines uns unverständlichen Phänomens annimmt, und unter den Eigenschaften des
„Lebens“ nach ihm sucht, scheint es mir einfacher, sich von der Möglichkeit der Existenz eines Raumes überzeugen zu lassen, in dem geometrisch rechte Isomere chemisch stabil sind, während sich linke Isomere in chemischen Prozessen anhäufen könnten.

L. Pasteur vermutete die Existenz eines solchen Raums. Im wesentlichen nahm er an, daß es hierbei zwei analoge Räume – gewissermaßen zwei Isomere – im Kosmos gebe: rechts und links. Er hielt diesen Raum für Euklidisch.

Aber im Euklidischen Raum sind Rechts- und Linkshändigkeit zwangsläufig geometrisch äquivalent. Es müßte eine Ursache für die Teilung des Raums in Links und Rechts als zwei unabhängige Räume geben. Pasteur ging empirisch vor, basierend darauf, wie racemische Kristalle und Moleküle in optische Isomere zerfallen. Aber bis auf den heutigen Tag kennen wir dieses Phänomen nur in lebenden Organismen oder in ihrer Anwesenheit. Tatsächlich führte Pasteur in seiner letzten Arbeit die spontane Aufteilung während der Kristallisation einer racemischen Säure in rechte und linke Weinsäure auf die Anwesenheit unsichtbarer Organismen in der Lösung zurück. Er meinte, daß Experimente, wie sie bisher noch niemand unternommen hätte, entworfen werden müßten, um diese Frage zu klären.

Die Vorstellung, daß so etwas im Euklidischen Raum mit ungeradzahligen Dimensionen möglich sei, scheint aus Gründen unwahrscheinlich, die sich ergeben, wenn man annimmt, die Identität von Rechts- und Linkshändigkeit sei eine geometrische Eigenschaft des dreidimensionalen Raums. Dies zeigt sich an der identischen Stabilität von Materiestrukturen aus der gleichen chemischen Verbindung mit entweder rechten oder linken Helixspiralen homologer Atompunkte, die den Raum vollständig ausfüllen. Solange Rechts-und Linkshändigkeit nicht als geometrische Eigenschaft des dreidimensionalen Euklidischen Raums untersucht wurden, glaube ich diese Aussage als Prämisse in meine Überlegungen aufnehmen zu dürfen.

Abgesehen von Strahlung nichtmaterieller Natur, gibt es Beispiele dreidimensionaler Räume, in denen eine solche Trennung von rechten und linken Räumen ohne weiteres vorkommt. Pasteur lenkte bereits die Aufmerksamkeit darauf und dachte, man könnte mit ihrer Hilfe ein Medium für die Urzeugung schaffen. Ein gasförmiges Medium oder Vakuum, mit Licht rechter oder linker elliptischer oder kreisförmiger Polarisation beleuchtet, wäre ein solcher Raumzustand. Hier haben wir es mit zwei getrennten Medien zu tun – rechts oder links. Aber bei Lebewesen geht es um ein stoffliches, kein energetisches Medium. Nur ein Experiment kann diese Frage klären. Leider wurden diese relativ leicht zugänglichen Phänomene experimentell überhaupt nicht untersucht.

Wenn dies der Stand unseres Wissens ist, scheint es mir bei geometrischen Problemen, die sich während der gesamten menschlichen Existenz in ihrer Grundannahme empirisch bestätigt haben und von der Menschheit konstruiert wurden, logisch korrekter zu sein, die materiellen und energetischen Raumzustände bei Körpern mit Blick auf ihre logischen Folgen nicht gleichzusetzen.

Ich werde deswegen von der Annahme ausgehen, daß das äquivalente Auftreten von Rechts- und Linkshändigkeit für Naturkörper in dem von ihnen eingenommenen Raum eine geometrische Eigenschaft des dreidimensionalen Euklidischen Raums ist.

Das Fehlen dieser Äquivalenz und das markante Auftreten der Linkshändigkeit im Stoffsubstrat lebender Materie und der Rechtshändigkeit in deren Funktionen zeigen, daß der von lebender Materie eingenommene Raum nicht der Euklidischen Geometrie entsprechen dürfte.

Bevor wir zu diesem Thema übergehen, müssen wir das Problem der Symmetrie, die für lebende Materie kennzeichnend ist, besprechen.

7. Das Problem der Symmetrie als Kennzeichen lebender Organismen läßt sich in den Grenzen der Symmetrie, die für Kristallkörper entwickelt wurde, absolut nicht lösen. Diese so augenfällige Symmetrie muß im wesentlichen auf andere Weise ausgedrückt werden.

Es ist so, daß man in der Morphologie lebender Organismen keine geraden Linien sieht. Wo man sie zum Beispiel bei Schwämmen oder Radiolaria antrifft, dann nur, wenn dabei Kristallisationsphänomene im Spiel sind. Gleichzeitig stoßen wir hier auf Beispiele von Fünffachsymmetrie wie etwa beim Seestern oder Ophiuroidea.

Dieser gesamte Bereich von Phänomenen, bei dem es eindeutig um Geometrie und Symmetrie geht, befindet
sich immer noch im Stillstand und wir haben keinen Weg gefunden, ihn mathematisch auszudrücken.

Alle an der Form lebender Organismen interessierten Forscher haben ihre Aufmerksamkeit auf zwei außergewöhnlich charakteristische Phänomene gerichtet. Das erste ist ihre Dispergiertheit, d. h. die scharfe Abgrenzung von ihrer Umwelt, in der sie geometrische Körper darzustellen scheinen, die unabhängig, in ständiger Bewegung und scharf von ihrer Umgebung abgesetzt sind. Es ist, als seien sie spezielle, kleine fremde Welten. Ihre Größe bewegt sich zwischen 10^–6 Zentimeter bis 10³ Zentimeter. Ihre Abgrenzung von der Umwelt ist ungewöhnlich auffällig und außerhalb jeden Zweifels. Die von den Körpern lebender Organismen eingenommenen Raumzustände unterscheiden sich grundlegend von den Raumzuständen inerter Naturkörper der sie umgebenden Biosphäre. Lebende Organismen werden in der Biosphäre nur von lebenden Organismen erzeugt. Niemals von inerten Körpern der Biosphäre.

Ihre Abgrenzung hat eine deutlich regelmäßig und symmetrische Form, und sie sind immer durch gekrümmte Flächen begrenzt. Es hat Versuche gegeben, diese Form als Ausdruck von Teilchenkräften zu erklären, die sich an der Grenze des gasförmigen und flüssigen Mediums entwickeln, in welchem die Organismen existieren und mit dem sie durch die ständige biogene Wanderung von Atomen verbunden sind. Ihre Form ist ungewöhnlich konstant, im historischen Zeitablauf extrem stabil und im Verlauf der geologischen Zeit unveränderlich: bei bestimmter lebender Materie ist sie über Hunderte von Millionen Jahren unverändert geblieben.

Diese Formstabilität, die in lebender Materie für uns im wesentlichen die ständige Bewegung von Atomen ausdrückt, und das dynamische Gleichgewicht von Atomen, das durch diese Bewegung ständig erhalten bleibt
– in Form eines Organismus, nicht eines Mechanismus –, lassen sich prinzipiell nicht vollständig durch Oberflächenkräfte bestimmen, sondern sind grundlegend von tieferen Materieeigenschaften (auf der Ebene von Atomen oder gar Isotopen) abhängig. Die allgemeine Ähnlichkeit damit, wie sich Teilchenkräfte äußern, hat mit der Tatsache zu tun, daß sich die Substanz eines lebenden Organismus, der hautsächlich aus flüssigem Wasser besteht, in einem kolloidalen oder kristallinen Zustand befindet; nur ein Teil der dispergierten Teilchen darin besteht aus kristalliner Materie, obgleich diese eine sehr große Rolle spielen dürfte.

Die Symmetrie, die beobachtet wird, und die Stabilität winzigster morphologischer Besonderheiten im Verlauf der geologischen Zeit, die in unserer experimentellen Arbeit ungewöhnlich ist, zeigt klar, daß hier tiefere Phänomene als Teilchenkräfte grundlegend sind.

Es ist daher vollkommen legitim anzunehmen, daß wir es hier mit einer Erscheinung tieferer Materieeigenschaften oder vielmehr mit einer Erscheinungsform der Materie zu tun haben, die sogar außerhalb der Eigenschaften von Atomen und Isotopen oder physikalisch-chemischen Eigenschaften im allgemeinen liegt.

Es ist außerdem legitim, die Arbeitshypothese aufzustellen und zu prüfen, daß lebende Materiekörper durch den geometrischen Zustand des von ihnen eingenommenen Raums grundlegend bestimmt sind, welcher sich vom Euklidischen Raum der inerten Naturkörper der Biosphäre unterscheidet.

Dieser Raum kann nicht Euklidisch sein, schon weil ihm die Äquivalenz zwischen Rechts- und Linkshändigkeit fehlt, die für den Euklidischen dreidimensionalen Raum unabdingbar ist.

8. Wir können die geometrischen Eigenschaften dieses Raums festzustellen versuchen. Die folgenden Eigenschaften des Riemannschen Raums erlauben uns anzunehmen, daß er mit einem oder mehreren dieser Raumzustände übereinstimmt. Erstens, die Tatsache, daß es eine unendliche Zahl Riemannscher Räume geben kann. Zweitens, daß jeder Riemannsche Raum geschlossen, aber doch unbegrenzt erscheint. Im dreidimensionalen Euklidischen Raum erscheint er als Kugel. Er hat somit keine geraden Linien noch ebene Flächen, sondern nur gekrümmte Linien und gekrümmte Flächen können vorkommen.

Wie wir wissen, gibt sich die Symmetrie lebender Materie innerhalb des inerten dreidimensionalen Euklidischen Raums der Biosphäre geometrisch auf genau diese Weise zu erkennen.

Die Dispergiertheit lebender Materie und das verbreitete Vorkommen geschlossener gekrümmter Flächen, die nahezu kugelförmig oder von geometrisch verwandten Formen sind, unterstützen diese Hypothese vollkommen.

Aber die geometrische Darstellung dieser Riemannschen Räume, die für lebende Materie kennzeichnend sind, läßt sich vertiefen.

9. Ihre Kennzeichen müssen sein:

1. In Formen, die dieser Körpergeometrie entsprechen, sind gerade Linien und ebene Flächen auf eine sekundäre Ebene verwiesen. Im Vordergrund stehen gekrümmte Flächen und gekrümmte Linien. Offenbar ist es bei den einfachsten Fällen im dreidimensionalen Euklidischen Raum zweck- Bemerkung zu diesen Aufsätzen
   mäßig, von Linien auf der Oberfläche einer Kugel und statt ebener Flächen von Abschnitten seiner gekrümmten Fläche auszugehen.
2. Vektoren in diesem Raum müssen polar und enantiomorph sein.
3. Rechts- und Linkshändigkeit müssen ausgeprägt sein, und sie sind geometrisch und physikalisch-chemisch nicht äquivalent. Offensichtlich ist die Linkshändigkeit in den inneren Strukturen lebender Körper vorherrschend.
4. In einem solchen Raum muß die Zeit geometrisch – genauso wie physikalisch-chemische Prozesse – durch einen polaren Vektor ausgedrückt werden.
5. Daraus folgt eine Reihe sehr wichtige Konsequenzen, die das Substrat lebender Materie, d. h. den Zustand ihres Raums, scharf vom Raumzustand inerter Körper unterscheiden. Die durch einen polaren Vektor ausgedrückte Zeit ist in den physikalisch-chemischen und biologischen Prozessen dieses Raums irreversibel; sie läuft nicht rückwärts. Hieraus folgt, daß in der Umgebung von Materie Entropie keinen Platz haben wird.
6. Aber ein Vektor in diesem Raum muß nicht nur polar sein, da er sich in den physikalisch-chemischen und biologischen Eigenschaften, die mit Materie einhergehen, ausdrückt. Er muß auch enantiomorph sein, ansonsten wäre Rechts- und Linkshändigkeit unmöglich.
7. Dieser Enantiomorphismus drückt sich in Phänomenen, die „in Richtung der Sonne“ oder „gegen die Sonne“ verlaufen, deutlich anders aus, was mit der Ungleichheit von Rechts- und Linkshändigkeit verbunden ist.
8. Die Biosphäre repräsentiert eine Hülle der Erde, in der in den Raumzuständen inerter Naturkörper mit ihrer dreidimensionalen Euklidischen Geometrie auf dispergierte Weise und in dispergierter Form zahllose winzige Riemannsche Räume lebender Materie eingeschlossen sind. Die Verbindung zwischen ihnen wird nur durch den ständigen biogenen Fluß von Atomen aufrechterhalten.

---

Bemerkung zu diesen Aufsätzen

Auf S. 442 von Filosofskie knigi naturalista (Die philosophischen Bücher eines Naturforschers), Nauka, Moskau 1988, berichten die Herausgeber, daß der darin enthaltene Text, den wir als Quelle benutzt haben, auf einer Kopie gründet, die im Archiv der sowjetischen Akademie der Wissenschaften f. 518, op. 1, Nr. 152 aufbewahrt wird. Die Herausgeber fügen hinzu: „Das Werk existiert als zwei Fragmente mit dem gleichen Titel, wovon das erste offenbar ein erster Entwurf ist. Diese Version wurde vom Autor später auf die Seite gelegt, was ihre Kürze [sic! Tatsächlich ist es länger] und ihren offensichtlichen unfertigen Charakter erklärt. Das zweite Fragment ist eher dichter und behandelt das Problem zusammen mit den von W. I. Wernadskij im Sanatorium Uskoje im Sommer 1938 gemachten Bemerkungen recht umfassend.“ Der Verweis auf die Schriften von 1938 aus Uskoje bezieht sich auf den Aufsatz „Über die Unterschiede zwischen lebenden und nichtlebenden Naturkörpern in der Biosphäre“, der auf deutsch in FUSION, Heft 3/2000 erschienen ist.

1. Der in Filosofskie knigi naturalista (Die philosophischen Bücher eines Naturforschers) enthaltene Text, Nauka, Moskau 1988, fügt hier ohne Angabe der genauen Stelle zwei Sätze ein, die Wernadskij auf einem separaten Blatt Papier getippt hat. „Aber ich kann die Betrachtung dieses Gebiets der Physik weglassen, welches unsere grundlegendsten Begriffe über das Universum enthält, genauso wie es in der heutigen wissenschaftlichen Arbeit in Physik und Chemie und nicht nur in der beschreibenden Naturwissenschaft praktisch ignoriert wird. Sie ist an einem Scheideweg und verändert sich fast täglich.“ [↩]
2. Wernadskij verwendet in diesem Aufsatz die Begriffe „dispersny“ und „dispersno“ in einem Sinn, der der „dispersen Phase“ des Chemikers entspricht, bei der Teilchen (als kolloidale Teilchen) oder Tröpfchen eines Stoffs in einem anderen Stoff verteilt sind, ein Zustand, der „diskontinuierliche Phase“ genannt wird. Wir haben uns entschlossen, „dispergiert“ anstelle möglicher Alternativen wie „quantisiert“ oder „diskret“ zu benutzen.[↩]
3. Im Text von Filosofskie knigi naturalista a.a.O. heißt es hier „v vyiawlenii“ (ihre Erkennung), aber Inhalt und Zusammenhang erfordern „v proiawlenii“. [↩]
4. Anmerkung des Autors: Diese Denkrichtung wurde in den Arbeiten von N. S. Kurnakow, N. I. Stepanow und der Schule von N. S. Kurnakow sehr erfolgreich zur Korrelierung chemischer Verbindungen angewendet.[↩]
5. In einer von uns zu Rate gezogenen Ausgabe wurde „benutzen“ mit „ignorieren“ ersetzt, aber in Wernadskijs Manuskript steht „ispol’sowat“, was „benutzen“ heißt.[↩]