Eine pädagogische Übung

---

Die Tatsache, daß das transatlantische Finanzsystem immer mehr wie Edgar Allan Poes Geschichte „Ein verbrauchter Mann“ erscheint, ist – um die Formulierung eines etwas anderen früheren US-Präsidenten zu entlehnen – eine gute Sache, keine schlechte Sache. Es bedeutet, daß wir die Chance haben, es durch etwas zu ersetzen, das tatsächlich funktionieren würde, um unseren Kindern und Kindeskindern eine Zukunft zu sichern.

Daß es sich in der Tat um eine Systemkrise handelt, zeigt die einfache Wahrheit, daß jedes Mal, wenn versucht wird, die Krise innerhalb der Regeln dieses Systems zu lösen, sie nur noch schlimmer wird. Jede Rettungsaktion verschiebt und vergrößert nur die Geschwindigkeit und die Auswirkungen des unvermeidlichen schockartigen Zusammenbruchs, sobald dieser wirklich eintritt.

Was ist also zu tun?

Der erste Schritt besteht darin, zuzugeben, daß es sich um ein systemisches Problem handelt – daß die Wurzeln und nicht nur ein einzelner Zweig jenes stolzen Baumes des Wirtschaftsliberalismus das Problem, ja sogar die Ursache der aktuellen Krise sind. Die Sophistik, die im antiken Athen grassierte, verbreitet sich heute über große Teile der westlichen Zivilisation. Der Sozialdarwinismus – „Macht schafft Recht“ – und der Wirtschaftsrelativismus – „Wenn man glaubt, es habe einen Wert, dann hat es einen Wert!“ – waren die willkommenen Rechtfertigungen dafür, die Realwirtschaft kaputt zu machen und gleichzeitig das Wachstum von Versprechungen auf zukünftigen monetären Reichtum als Daseinsberechtigung der Gesellschaft zu proklamieren. „Aber nimmt das BIP nicht zu? Ist unsere Gesellschaft nicht reicher geworden?“, mag mancher einwenden, worauf wir antworten sollten: Nur der Leichtgläubige nimmt die Versprechungen eines Hochstaplers als verläßliches Fundament, auf dem er die Zukunft seiner Kinder baut.

Erkennen wir also, daß wir betrogen wurden, werfen wir die sophistische Philosophie über Bord und wenden wir uns statt dessen der Qualität des Denkens zu, die die großen Köpfe der Vergangenheit angetrieben hat, deren Entdeckungen und Erfindungen die „unsichtbaren Bausteine“ sind, auf denen unsere Gesellschaft heute steht.

Was treibt den großen Denker an?

Was war es, das Denker wie Dmitri Mendelejew¹, Albert Einstein² oder Komponisten wie Johann Sebastian Bach antrieb? Stand hinter ihren revolutionären Entdeckungen und Kompositionen lediglich ein darwinistischer Überlebens- und Beherrschungsimpuls? Hat das Streben nach Reichtum und sinnlicher Befriedigung sie dazu gebracht, sich mit den unsichtbaren Ursachen der Welt zu beschäftigen? Oder hat ihre Suche nach Ruhm und Anerkennung sie dazu gebracht, allgemein akzeptierte Auffassungen umzuwerfen? Offensichtlich nicht.

Was hat sie also angetrieben? Einige von ihnen haben sich selbst hierzu geäußert:

„Dies ,sich wundern‘ scheint dann aufzutreten, wenn ein Erlebnis mit einer in uns hinreichend fixierten Begriffswelt in Konflikt kommt… Ein Wunder solcher Art erlebte ich als Kind von 4 oder 5 Jahren, als mir mein Vater einen Kompaß zeigte. Daß diese Nadel in so bestimmter Weise sich benahm, paßte so gar nicht in die Art des Geschehens hinein, die in der unbewußten Begriffswelt Platz finden konnte (an ,Berührung‘ geknüpftes Wirken). Ich erinnere mich noch jetzt – oder glaube mich zu erinnern –, daß dies Erlebnis tiefen und bleibenden Eindruck auf mich gemacht hat. Da mußte etwas hinter den Dingen sein, das tief verborgen war.“ (Albert Einstein)³

„Daß die Bewegungen der Planeten kreisartig sind, wird dadurch bezeugt, daß sie sich ständig wiederholen. Die Vernunft, die diese Wahrheit der Erfahrung entnimmt, nimmt nun sogleich von vornherein an, daß ihre Umläufe vollkommene Kreise sind; denn unter den ebenen Figuren wird der Kreis, unter den Körpern das Himmelsgewölbe für das vollkommenste Gebilde gehalten. Sobald aber bei aufmerksamer Beobachtung die Erfahrung etwas anderes zu lehren scheint, daß nämlich die Planeten von der einfachen Kreisbahn abweichen, entsteht höchste Verwunderung, wodurch schließlich die Menschen dazu getrieben wurden, die Ursachen hiervon zu erforschen.“(Johannes Kepler)⁴

Erst wenn unsere Neugierde den Weg weist und unser Innerstes vom Staunen ergriffen wird und nicht mehr loslassen kann, erst dann kann sich Kreativität entfalten. Im Hintergrund mögen Stimmen eines bequemen Egoismus zu hören sein, die einen warnen, nicht mit Fremden zu sprechen – aber solche Stimmen muß man ignorieren, sich öffnen und sein wahres Ich walten lassen.⁵

Wie hier von Kepler und Einstein beschrieben, wird unsere Neugierde durch etwas provoziert, das mit unserem Verständnis der Welt unvereinbar ist. Es provoziert uns, nicht so sehr nach außen auf die Welt unserer Sinne zu schauen, sondern nach innen auf die Annahmen, nach denen wir diese Wahrnehmungen ordnen. Erst wenn man den Grund für die Inkonsistenz isoliert, die schon immer existierte, aber bisher verborgen lag, wird der Blick frei auf den inneren Widerspruch – das Nebeneinander von Unvereinbarem. Ist dieser innere Widerspruch klar definiert, zwingt er den Verstand dazu, den Prozeß der Hypothesenbildung selbst „direkt“ zu betrachten.

Um ein solches Nebeneinander von mindestens zwei scheinbaren Unvereinbarkeiten auflösen zu können, muß notwendigerweise die Existenz aller dieser Unvereinbarkeiten erklärt werden, sozusagen als „schattenhafte Reflexionen“ eines höheren Bereichs. Als Beispiel hierfür ließe sich die Unvereinbarkeit der longitudinalen und der latitudinalen „Sichtpunkte“ der Marsbewegung⁶ anführen, die Kepler dazu zwang, Äquanten und Kreisbahnen zu verwerfen und durch seine Neue Astronomie zu ersetzen; oder Einsteins Vergleich des Gesetzes der konstanten Lichtgeschwindigkeit im Vakuum mit dem Relativitätsprinzip (d. h. jedes physikalische Gesetz muß für jeden Beobachter gleichermaßen gelten), was ihn zur Entdeckung der relativistischen Natur von Raum und Zeit führte; oder sogar auch Bachs fugale „Gegenüberstellung“ verschiedener Stimmen, wodurch sich eine höhere polyphone Einheit entwickelt, wozu auch die Hingabe erforderlich ist, um ein solches Ergebnis zu erzielen. Hieran erkennt man den subjektiven Kampf mit einem wissenschaftlichen Paradox, was in diesem Sinne ein Bild für den kreativen Prozeß selbst ist. Hier werden wir ein anderes Bild im gleichen Sinne verwenden.

Eine pädagogische Übung

Die folgende Abhandlung mag zunächst zwar etwas abstrakt erscheinen, doch die Idee sollte im weiteren Verlauf immer klarer werden.⁷ Wir werden nicht nur einen Teil der Grundlage für Gauß‘ Entdeckung des komplexen Bereichs⁸ darstellen, sondern es sollte auch gelingen, etwas über die Natur der Beziehung zwischen menschlicher Kreativität und Wirtschaft auszusagen, womit das Dogma der liberalen „Freihandels“-Ökonomie ersetzt werden muß.

Wie in den obigen Beispielen werden wir zwei scheinbar unvereinbare „Sichtweisen“ desselben Prozesses (im Bereich der Zahlen) gegenüberstellen: nämlich das arithmetische Wachstum und das geometrische Wachstum – wobei ersteres einen konstanten Abstand zwischen jedem Schritt als „Einheit“ seiner Sichtweise hat (1, 2, 3, 4,…; 2, 4, 6, 8,… usw.), während die letztere Sichtweise ein konstantes Verhältnis oder einen Faktor zwischen jedem Schritt als „Einheit“ hat (1, 2, 4, 8, 16,…; 1, 3, 9, 27, 81,… usw.).⁹ Wir werden ihre Unvereinbarkeit (d. h. den Umstand, wie sie nicht zueinander passen) zum Schwerpunkt unserer Untersuchung machen.

Machen wir uns also bereit, um – wie es in Bachs Motette Jesu meine Freude heißt – „dem alten Drachen zu trotzen“, und krempeln wir die Ärmel hoch. Am Ende – wie bei jeder kreativen Arbeit – werden wir zurückblicken und schmunzeln, und uns fragen, warum wir es so schwer fanden.

Reste

(Nota bene: Im folgenden sollte der Leser immer selbst rechnen – also: keinen Taschenrechner! Dies ist ein integraler Bestandteil der hier vermittelten Gesamtidee).

Beginnen wir mit der folgenden geometrischen Wachstumsreihe:

2, 4, 8, 16, 32, 64, 128, 256, usw.

Stellen wir dem das arithmetische Wachstum von 5 gegenüber:

5, 10, 15, 20, usw.

Das heißt, man teile die Verdoppelungsreihen durch 5 und betrachte den sich ergebenen Rückstand oder Rest – ein Ausdruck ihrer Unvereinbarkeit:

2	4	8	16	32	64	128	256	512
2	4	3	1	2	4	3	1	2

Die erste Zeile ist die Verdopplungsreihe, die zweite Reihe sind die Reste nach Teilung der ersten Reihe durch 5.

Schauen wir uns nun die Reste an: Gibt es ein Muster? Es ist ein deutliches zyklisches Muster erkennbar.

Versuchen wir es mit einer anderen Art des geometrischen Wachstums (Verdreifachung), ebenfalls geteilt durch 5:

3	9	27	81	243	729	2187	6561	19.683
3	4	2	1	3	4	2	1	3

Auch hier ergibt sich ein klares zyklisches Muster. Warum ist das so? Und warum ist 1 immer der letzte Rest, bevor es wieder von vorne losgeht? Vielleicht hat es etwas damit zu tun, daß wir die Zahl 5 als arithmetische Einheit verwenden. Versuchen wir stattdessen, die gleiche Art geometrischen Wachstums mit dem arithmetischen Wachstum von 7 zu erzeugen. Allerdings wird dabei die Berechnung der Reste viel schwieriger. Auch hier ist es wichtig, daß sich der Leser diese Schwierigkeit selbst erarbeitet.

2	4	8	16	32	64	128	256	512
2	4	1	2	4	1	2	4	1
3	9	27	81	243	729	2187	6561	19.683
3	2	6	4	5	1	3	2	6

Nein! Für 7 gilt dasselbe. Sowohl der zyklische Charakter als auch die Rolle von 1 bleiben erhalten, obwohl der Zyklus bei der Verdopplung kürzer ist als der Zyklus bei der Verdreifachung. Auch dies wird sich als eine gewisse Gesetzmäßigkeit – wenn auch keine lineare – erweisen, wenn wir mit größeren Zahlen zu arbeiten beginnen. Doch zuvor wollen wir versuchen, die Frage zu beantworten, warum diese regelmäßigen Zyklen auftreten.

Wenn wir die Beziehungen zwischen den Resten in der Verdopplungsreihe betrachten, sehen wir, daß diese einen bestimmten Charakter mit der ursprünglichen Verdopplungsreihe gemein haben. 1 zu 2 ist eine Verdopplung, ebenso wie 2 zu 4. 4 verdoppelt ist 8, was geteilt durch 7 den Rest 1 ergibt, und der Prozeß beginnt von vorne. Nehmen wir dieselbe Verdopplungsreihe, dividieren sie aber durch 5: 1 zu 2 und 2 zu 4 sind Verdoppelungen. 4 verdoppelt ist 8, aber wenn wir durch 5 statt durch 7 teilen, bleibt 3 als Rest übrig. Verdoppelt man entweder 8 (aus der ursprünglichen Reihe) oder ihren Rest, 3, erhält man entweder 16 oder 6, die beide 1 als Rest haben, wenn man durch 5 dividiert, und der Zyklus beginnt von neuem. Obwohl sich also die Reihe der Reste deutlich von der ursprünglichen Reihe unterscheidet, bleibt die Eigenschaft der Verdopplung durchgehend erhalten. Ist dies auch bei der Serie der Verdreifachung der Fall? (Der Leser sollte dies selbst herausfinden.)

Nachdem wir festgestellt haben, daß dies der Fall ist (tatsächlich?), könnten wir beim Nachdenken darüber feststellen, daß dies durchaus Sinn macht: Wenn der Teil der Zahl, der durch 7 teilbar ist (z. B. 14 von 16), verdoppelt wird (z. B. 28 von 32), dann ist dieser Teil auch durch 7 teilbar; der Teil, der übrig bleibt, ist dann, wenn er verdoppelt wird, der doppelte Rest (z. B. 4 ist das Doppelte von 2). Dasselbe ist der Fall für 3 oder jede andere Basis. Und wenn man bedenkt, daß die Reste nie größer als der Teiler sein können, reichen diese beiden Überlegungen aus, um die zyklische Natur der Reste zu verstehen. Dieser Gedankengang sollte auch ausreichen, um herauszufinden, welche Rolle die 1 spielt (auch das überlassen wir dem Leser).

Dies bringt einen Vorteil in unserer weiteren Untersuchung: Da es ausreicht, die Reste zu verdoppeln, zu verdreifachen usw., können wir nun die ursprüngliche Reihe der Verdopplung, Verdreifachung usw. außer acht lassen und uns einfach auf die Reste konzentrieren. Diese Entdeckung erhöht sowohl die Geschwindigkeit als auch die Präzision (geringere Fehlerwahrscheinlichkeit), mit der wir die Reste erzeugen können, und erfordert gleichzeitig insgesamt weniger Aufwand – mehr zu dieser ökonomischeren Kuriosität später.

Berechnen wir nun die übrigen Reste, die das arithmetische Wachstum mit der Einheit 7 auf die Vervierfachung, Verfünffachung und Versechsfachung beziehen (der Leser sollte mitrechnen):

1	2	4	1	2	4	1
1	3	2	6	4	5	1
1	4	2	1	4	2	1
1	5	4	6	2	3	1
1	6	1	6	1	6	1

Jede dieser Zeilen sind lediglich die Reste, wobei wir die ursprünglichen Reihen weglassen, da diese nicht mehr benötigt werden. Wir beginnen mit 1, um die Zyklen von Anfang bis Ende zu verdeutlichen. Man bedenke, wie einfach das ist, verglichen mit der Berechnung von 5⁶ und der anschließenden Teilung dieser Zahl durch 7!

Doch nun zum nächsten Schritt: Nehmen wir die 17 als unsere arithmetische Wachstumseinheit und vergleichen sie mit dem geometrischen Wachstum aller Zahlen darunter. Beginnen wir einfach mit 2 und 3:

1	2	4	8	16	15	13	9	1	2	4	8	16	15	13	9	1
1	3	9	10	13	5	15	11	16	14	8	7	4	12	2	6	1

Das ist zwar viel einfacher, als z. B. 3¹⁶ zu berechnen und durch 17 zu dividieren, aber selbst das Rechnen mit den Resten allein wird schnell anstrengend. Muß man vielleicht mehr über den Charakter der Reste verstehen, um unsere Fähigkeit noch weiter zu verbessern, mit diesen Zahlen zu arbeiten? Schauen Sie sich noch einmal das Beispiel mit 7 von vorhin an, insbesondere die Restereihen von 3 und 5. Fällt Ihnen etwas auf? Schauen Sie genau hin, bevor Sie weiter lesen.

Haben Sie es gefunden? Sie sind die exakten Spiegelbilder voneinander! 5 (Verfünffachung) ist 3 (Verdreifachung), nur in umgekehrter Richtung. Das gilt auch für 2 und 4. Mit welcher Zahl endete die 3er-Reihe im Fall von 17? Sie endete mit der Zahl 6. Könnte die 6er-Reihe dann die 3er-Reihe spiegeln? Versuchen Sie, die ersten Reste für 6 zu berechnen und schauen Sie, ob es funktioniert.

Warum ist das so? Darüber sollte der Leser selbst nachdenken, und wir machen hier einfach von dieser neu entdeckten Eigenschaft Gebrauch, um die restlichen Reste für 17 zu erzeugen (wie immer sollte der Leser mitrechnen!):

(Hinweis: Der Buchstabe a steht für die jeweilige Potenz einer Zeile. Zum Beispiel a = 2 für die Zeile der Verdopplungen, wobei der Rest von 2⁵ = 15 ist, usw.)

a0	a1	a2	a3	a4	a5	a6	a7	a8	a9	a10	a11	a12	a13	a14	a15	a16
1	2	4	8	16	15	13	9	1	2	4	8	16	15	13	9	1
1	3	9	10	13	5	15	11	16	14	8	7	4	12	2	6	1
1	4	16	13	1	4	16	13	1	4	16	13	1	4	16	13	1
1	5	8	6	13	14	2	10	16	12	9	11	4	3	15	7	1
1	6	2	12	4	7	8	14	16	11	15	5	13	10	9	3	1
1	7	15	3	4	11	9	12	16	10	2	15	13	6	8	5	1
1	8	13	2	16	9	4	15	1	8	13	2	16	9	4	15	1
1	9	13	15	16	8	4	2	1	9	13	15	16	8	4	2	1
1	10	15	14	4	6	9	5	16	7	2	3	13	11	8	12	1
1	11	2	5	4	10	8	3	16	6	15	12	13	7	9	14	1
1	12	8	11	13	3	2	7	16	5	9	6	4	14	15	10	1
1	13	16	4	1	13	16	4	1	13	16	4	1	13	16	4	1
1	14	9	7	13	12	15	6	16	3	8	10	4	5	2	11	1
1	15	4	9	16	2	13	8	1	15	4	9	16	2	13	8	1
1	16	1	16	1	16	1	16	1	16	1	16	1	16	1	16	1

6 ist das Spiegelbild von 3, 9 von 2, 13 von 4, usw., aber nicht nur das. Wenn wir, anstatt die Reihe von 3 rückwärts zu betrachten, jeden dritten Schritt (1, 10, 15, 14, usw.) wählen, entspricht die Reihe von 10 genau dieser Reihe! Wir können nun alle Reste ausschreiben, einfach von einer Zeile ausgehend, deren Zyklus sich bis zur Spalte a¹⁶ nicht wiederholt (bis 1 als Rest zurückkehrt). Was für ein Unterschied zum Ausrechnen von 14¹⁶ und dem Dividieren durch 17, um den Rest zu finden!¹⁰

Nach dieser ersten Untersuchung legen wir vorerst eine Pause ein, denn sie reicht aus, um eine Grundlage für ein erstes Verständnis der Natur wirtschaftlicher Prozesse zu schaffen – ein Verständnis, das zum Baustein für ein neues, gerechtes Wirtschaftssystem werden muß.

Für alle, die weiter vorstoßen wollen, um die Einheit hinter den bisher untersuchten Unvereinbarkeiten besser zu verstehen, haben wir am Ende des Artikels einen Nachtrag hinzugefügt.

Ein neues wirtschaftliches Maß

Blicken wir nun auf den gesamten Prozeß zurück, den wir gerade durchlaufen haben. Zweimal entdeckten wir etwas über die Natur der zur Debatte stehenden Gegenüberstellung (durch ihren Schatten, die Reste): Erstens entdeckten wir, daß sich der geometrische Charakter in den Resten selbst widerspiegelt; und zweitens entdeckten wir, indem wir diese Beziehung zwischen den so erzeugten geometrischen Reihen nutzten, wie man die gesamte „Familie“ erzeugen kann. Beide Male erhöhte sich unsere Fähigkeit, die Reste zu generieren: Wir konnten sie nun schneller und mit zunehmender Präzision erzeugen, während wir gleichzeitig den dafür erforderlichen Aufwand reduzierten. Dies ist eine sehr brauchbare, erste Annäherung an das, was man unter ökonomischem Wert verstehen sollte: die Steigerung des produktiven Potentials der Gesellschaft durch neue Entdeckungen und Erfindungen und deren Anwendung im Produktionsprozeß.¹¹

Wir ringen mit einem paradoxen Problem, lassen nicht locker und erkennen schließlich das höhere Prinzip, das hinter dem Paradox steckt. Wenden wir diese neue Einsicht an, erhöhen wir unsere Macht nicht nur über den betreffenden Prozeß, sondern auch über oft scheinbar nicht verwandte Prozesse. Mit anderen Worten: Der physische Aufwand (Input) sinkt, während die Produktivität (Output) steigt.

Somit haben weder Materie, noch Energie, sondern Ideen die größte Macht in diesem Universum.¹² Tatsächlich sind Ideen und ihre Wirkungen, wie sie sich zum Beispiel in der Entwicklung neuer Technologien manifestieren, die einzigen Ursachen für wirtschaftliches Wachstum. Sie besitzen eine Macht, die tiefer liegt als der einfache mathematische Bereich, denn es können so Dinge aufgelöst werden, die logisch unvereinbar sind. Tatsächlich entwickelt sich die Mathematik – wie jede andere Sprache auch – infolge der Entwicklung dieser Macht. Die Logik setzt erst ein, wenn die Ausgangsbegriffe klar definiert sind. Mit Kreativität werden diese Ausgangsbegriffe stets von einem immer tieferen, ontologischen Standpunkt aus neu definiert, und die mathematische Sprache, die darauf angewendet werden soll, muß von diesem neuen, höheren Standpunkt aus entwickelt werden.

Kein Wunder, daß die Wissenschaftsgemeinschaft, die historisch in einem formalistischen Spinnennetz gefangen ist, jeden anfeindet und ausgrenzt, der es wagt, das Fundament ihres so geschätzten Gebäudes anzutasten.¹³

Ein neues Wirtschaftssystem

Anstatt die gegenwärtigen Finanzstrukturen zu retten, indem man die Realwirtschaft opfert – so wie man den Patienten opfern würde, um den Tumor zu retten, wie es z. B. das Bail-in-Konzept der New Yorker und Londoner Banker vorsieht¹⁴ –, muß genau das Gegenteil geschehen. Das Bankensystem muß entsprechend der oben verdeutlichten Definition ökonomischen Wertes reorganisiert und das Bank- und Finanzwesen lediglich als ein Werkzeug betrachtet werden, das dazu dient, das realwirtschaftliche Wachstum zu fördern. Das „wirtschaftliche Potential“ jedes Einzelnen muß die Bank- und Kreditpolitik bestimmen – die „Physik“ muß die Mathematik bestimmen.¹⁵

Wie von dem Ökonomen Lyndon LaRouche dargelegt,¹⁶ entspringen die zu ergreifenden Maßnahmen alle einer einzigen Vorstellung von menschlicher Kreativität als treibender Kraft im Wirtschaftsprozeß und müssen als solche umgesetzt werden.

Ohne eine nationale kreditschöpfende Institution würde die Einführung eines Glass-Steagall-Trennbankensystems und der Stopp der Rettungsgelder für die Großbanken zwar das Geschäftsbankensystem schützen, aber alle Derivatemärkte und alle daran angeschlossenen Großbanken würden unmittelbar implodieren, und die kreditausgezehrte Wirtschaft würde samt den Geschäftsbanken bald mit in den Abgrund gerissen werden. Ohne Glass-Steagall würden die neu generierten Kreditströme für neue Infrastruktur, für Wissenschafts-Crash-Programme und vieles mehr schließlich in das finanzielle schwarze Loch gesaugt werden, das die City of London, die Wall Street und ihre Offshore-Finanzparadiese heutzutage darstellen. Ohne ein klares Verständnis der zugrundeliegenden physikalischen Wirtschaftsprinzipien läßt sich der neu generierte Kredit nicht richtig handhaben, um genügend Produktivitätssteigerung zu erzeugen, d. h. den realwirtschaftlichen Breakeven zu überschreiten, was zu einem eventuellen, wenn auch verzögerten Zusammenbruch des Systems führt.

LaRouches Vier Gesetze haben eine Quasi-Tensor-Qualität, wobei jedes Element ein interner Kausalfaktor ist, der anderen Elementen eine wirksame Existenz ermöglicht. Sie sind reziproke Notwendigkeiten bzw. verhalten sich „ko-kausal“ zueinander und haben alle die „anti-lineare“ Idee menschlicher Kreativität als treibende Kraft hinter jeder gesunden Wirtschaft gemein. Nur wenn die Vier Gesetze auf diese Weise umgesetzt werden, funktionieren sie; wenn nicht, nicht.

Der Wert einer Wirtschaft ist weder ihre Währung, noch ihr Währungskorb, noch Gold, noch irgendein anderes greifbares Objekt; noch ist er relativistisch und willkürlich – so, wie sich die Märkte „anfühlen“. Im Mittelpunkt steht das schöpferische Potential jedes einzelnen Menschen – die noch zu verwirklichende Ursache für das zukünftige Wohlergehen einer besseren Gesellschaft, die all jenen gehört, die sie mit erschaffen haben.

Ein Nachtrag – der komplexe Bereich

Lassen Sie uns noch ein wenig tiefer in den Prozeß eindringen, den wir bisher untersucht haben, um die unsichtbare, vereinigende Geometrie hinter dem nur scheinbar Unvereinbaren zu betrachten.

Schauen wir uns noch einmal die letzte Tabelle der Reste an. Es gibt bestimmte Stellen in den Zeilen, die immer die gleichen Zahlen haben. In der Spalte a⁸ zum Beispiel findet man nur die 16 oder die 1. Wenn dort die Zahl 16 auftaucht, kommen interessanterweise in dieser Reihe stets alle Reste von 2 bis 16 vor. 16 liegt immer genau in der Mitte zwischen dem Rest 1 und dem nächsten Mal, wenn 1 als Rest auftaucht; in der Reihe der Verdreifachungen (a = 3) wird der Rest 1 zum Beispiel bei 3⁰ und 3¹⁶ gefunden, und der Rest 16 bei 3⁸.

16 ist übrigens auch –1 relativ zu 17; das heißt, 17 ist entweder um +16 (oder um –1) davon entfernt, die Zahl perfekt zu teilen (im Fall der Recheneinheit 7 spielt der Rest 6 oder –1 die gleiche Rolle wie der Rest 16 hier). Wenn man sich die Zyklizität der Reste im Zusammenhang mit der Idee anschaut, daß –1 auf halbem Weg zwischen 1 und der Rückkehr zu 1 liegt, bekommt man einen ersten Eindruck von der Geometrie, die dem Verhalten der Reste zugrunde liegt, nämlich dem Einheitskreis.

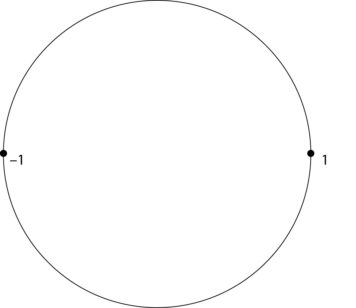
Aber gehen wir noch einen Schritt weiter. Was ist, wenn wir wieder die Mitte nehmen (also zwischen 1 und –1)? In der Reihe der Reste finden wir nur zwei Zahlen: 4 und 13. Wenn man nun bedenkt, daß wir es mit geometrischem Wachstum zu tun haben (wobei die Beziehung zwischen den Zahlen die „Einheit“ ist), entspricht der „halbe Weg“ hier der Quadratwurzel. Zum Beispiel ist die „Mitte“ zwischen 1 und 16 die √16, was 4 ergibt; oder anders ausgedrückt, 1 : √16 verhält sich wie √16 : 16. Aber 16 war auch –1 relativ zu 17. Und so stoßen wir auf unseren schwer faßbaren „imaginären“ Freund: √–1 als das geometrische Mittel zwischen 1 und –1 (oder 1 : √–1 verhält sich wie √–1 : –1).

 

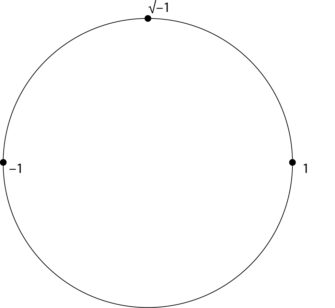
Vergleicht man diesen mit unserem Einheitskreis, sehen wir genau das: √–1 ist ein Viertel einer Umdrehung, also die Mitte zwischen 1 und –1 (was eine halbe Umdrehung ist); oder anders ausgedrückt, das Verhältnis zwischen 1 und √–1 bzw. zwischen √–1 und –1 ist dasselbe: eine 90-Grad-Drehung gegen den Uhrzeigersinn.

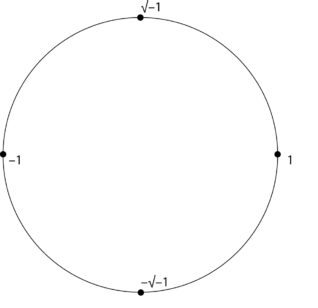
Um genau zu sein, sehen wir, daß es noch einen weiteren Punkt auf halbem Weg zwischen 1 und –1 gibt, nämlich –√–1. Wenn wir uns unsere Tabelle der Reste noch einmal ansehen, sehen wir, daß wir auch hier tatsächlich zwei Punkte auf halbem Weg zwischen 1 und –1 haben, nämlich 4 und 13, die beide die Negative voneinander sind, bezogen auf 17 als unsere arithmetische Einheit: 13 ist –4 und 4 ist –13. Weiterhin finden wir in den Reihen von 4 und 13 (entsprechend 4^1…16 und 13^1…16) nur die Reste (1, 4, 16, 13), wobei 1 und 16 ihre Plätze behalten und 4 und 13 die Plätze tauschen; dies entspricht unseren vier Schritten im Einheitskreis, die sich entweder im oder gegen den Uhrzeigersinn bewegen (von 1 zu √–1 zu –1 zu –√–1 zurück zu 1, oder von 1 zu –√–1 zu –1 zu √–1 zu 1).

Es läßt sich noch viel mehr hierzu sagen. In der Tat ist die gesamte Tabelle der Reste vollständig gesetzmäßig, wobei jeder Rest eine spezifische Rolle spielt. Die Hauptfrage bei dieser und auch jeder anderen Untersuchung ist immer das „Warum?“ Warum ist das so? Wie können wir die „Geometrie“ hinter dieser Gesetzmäßigkeit verstehen? Oder anders gefragt: Welches Konzept vereint die nur scheinbare Unvereinbarkeit von arithmetischem und geometrischem Wachstum?

Was wir hier zu erahnen beginnen, ist das, was Carl Gauß als „den Bereich der komplexen Zahlen“¹⁷ definiert hat, von dem der geometrische und der arithmetische Bereich nur Schatten sind. Versteht man diesen Bereich als realen physikalischen Bereich und nicht als trockene, formale Definition, wie es heutzutage üblich ist, lassen sich damit nicht nur alle „Pfade geringster Wirkung“ in einer physikalischen Mannigfaltigkeit ausdrücken (definiert durch eine gegebene Reihe universeller physikalischer Prinzipien, die sozusagen „tangential“ überall darauf wirken), sondern diese auch in noch höhere Mannigfaltigkeiten umwandeln, welche durch die Hinzufügung neu entdeckter physikalischer und sogar sozialer¹⁸ Prinzipien (oder „Dimensionen“) entstanden sind. Diese wiederum definieren die „Pfade geringster Wirkung“ in den ökonomischen Beziehungen neu. Bernhard Riemann, Gauß‘ wichtigster Schüler, schrieb, daß erst durch die Anwendung des komplexen Bereichs „eine sonst versteckt bleibende Harmonie und Regelmäßigkeit hervortritt.“¹⁹

Der Wirtschaftswissenschaftler Lyndon LaRouche hat viel über den komplexen Bereich und seine Bedeutung für die Wirtschaftswissenschaft geschrieben. Hier geben wir nur einen kurzen Auszug aus seiner Schrift Der wahre Staatsmann: Das historische Individuum²⁰ wieder:

„Der komplexe Bereich, wie ihn vor allem Gauß und Riemann mit ihrer Pionierarbeit definiert haben, liefert uns eine physikalische Geometrie realer Kräfte – ein reales Universum anstelle der Schattenwelt der naiven Sinneswahrnehmung. ,Imaginär‘ ist in Wirklichkeit nur die euklidische oder quasieuklidische ,Elfenbeinturm‘-Geometrie, die nur die Schatten einer realen physikalischen Geometrie sieht, aber nicht die physikalische Substanz, die sie wirft.“

– Lyndon H. LaRouche

Man könnte meinen, wir hätten nur abstrakte Beziehungen zwischen ganzen Zahlen untersucht, aber das waren nur die Schatten von etwas, das in Wirklichkeit sehr real und notwendig ist. Der komplexe Bereich hat nicht nur implizit die Fähigkeit, Transformationen auszudrücken, die die Existenzfähigkeit der menschlichen Gesellschaft erhöht, sondern er ist selbst eine Kraft, deren Beherrschung entscheidend ist für die Überwindung der gegenwärtigen Krise, mit der die Menschheit konfrontiert ist.

1. Der Entdecker der Periodensystems der Elemente, das die Grundlage für unser heutiges Verständnis sämtlicher chemischer Prozesse legte.[↩]
2. Seine berühmte Formel E = mc² legte die theoretische Grundlage für das Verständnis der Kernspaltung und der Kernfusion.[↩]
3. Einstein A. (1983) Autobiographisches. In: Schilpp P. A. (eds) Albert Einstein als Philosoph und Naturforscher. Facetten der Physik. Vieweg+Teubner Verlag, Wiesbaden.[↩]
4. Johannes Kepler, Astronomia Nova, Neue, ursächlich begründete Astronomie, übersetzt von Max Caspar, Marix Verlag, Wiesbaden, 2005, 1. Kapitel, S.79.[↩]
5. Siehe auch Lyndon LaRouche, Was Sie schon immer über Wirtschaft wissen wollten, Böttiger-Verlag, 1985, Kapitel 5.[↩]
6. Siehe das Video On Metaphor: an Intermezzo von Jason Ross: https://youtube/zPT21P4rEYQ[↩]
7. Eine Anregung wäre, die angeführten Beispiele in einer Gruppe durchzuarbeiten, um nicht allein darin stecken zu bleiben.[↩]
8. Die folgende Arbeit basiert auf Gauß‘ großem Werk, den Disquisitiones Arithmeticae.[↩]
9. Mit beiden Sichtweisen bzw. Ansätzen lassen sich alle ganzen Zahlen erzeugen. Bei der arithmetischen Reihe durch immer weiteres einfaches Addieren von +1, bei der geometrischen Reihe durch eine Kombination aller geometrischen Reihen. Zum Beispiel kann man weder mit der Reihe der Verdoppelungen noch der Verdreifachungen die Zahl 6 erzeugen, wohingegen dies mit der „Verdoppelung der Verdreifachung“, 2 ‧ 3, möglich ist. Wenn man alle Primzahlen auf diese Weise als „Bausteine“ verwendet, lassen sich alle ganzen Zahlen erzeugen. Zum Beispiel: 26 = 2 ‧ 13; 27 = 3 ‧ 3 ‧ 3; 28 = 2 ‧ 2 ‧ 7; usw. Wenn eine Zahl nicht aus anderen Primzahlen gebildet werden kann, ist sie selbst eine Primzahl.[↩]
10. Charakteristisch für diesen Ansatz war, daß Gauß einmal in einer Stunde die Bahn eines Kometen berechnete, für die Euler drei Tage gebraucht hatte – eine Arbeit, bei der Euler auf einem Auge seine Sehkraft verlor. „Ich wäre wahrscheinlich auch erblindet“, soll Gauß über Euler gesagt haben, „wenn ich bereit gewesen wäre, drei Tage lang auf diese Weise weiterzurechnen!“[↩]
11. Der Wirtschaftswissenschaftler Lyndon LaRouche hat diesen Anstieg des produktiven Potentials der Gesellschaft als die Fähigkeit der Gesellschaft definiert, eine wachsende Anzahl von Menschen auf einem höheren Lebensstandard in einem bestimmten Gebiet zu erhalten – d. h. die potentielle relative Bevölkerungsdichte. Mehr dazu finden Sie in seinem Buch Was Sie schon immer über Wirtschaft wissen wollten, a. a. O.[↩]
12. Waren es nicht Einsteins Ideen, die die Entfesselung der Fusionsenergie möglich machten?[↩]
13. Nach der bescheidenen Meinung dieses Autors sind Postulate wie dunkle Materie und dunkle Energie Erfindungen, um den Schein aktueller Theorien zu wahren – so wie es zu Keplers Zeit die Epizyklen waren –, anstatt zuzugeben, daß die beobachteten Paradoxien, wie die Rotationsgeschwindigkeit von Galaxien und die vermeintlich beschleunigte Expansion des Universums, mit den aktuellen Axiomen der Physik einfach unvereinbar sind. Wie Sokrates vielleicht eingeworfen hätte: „Bist du jetzt nicht glücklicher, da du weißt, daß du nichts weißt, als wenn du dachtest, du wüßtest es, aber es in Wirklichkeit nicht wußtest?“[↩]
14. https://larouchepub.com/other/2013/4031why_shut_wall_st.html[↩]
15. Bernhard Riemann, „Über die Hypothesen, welche der Geometrie zugrunde liegen“, Habilitationsschrift, 1854, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 13 (1868).[↩]
16. Lyndon H. LaRouche, „Vier neue Gesetze, um die USA zu retten: Keine Option, sondern unmittelbare Notwendigkeit“, Neue Solidarität, Nr. 10, 11. März 2021. https://www.solidaritaet.com/neuesol/2021/10/larouche-4gesetze.htm[↩]
17. Das ist nur ein Pfad, der zum komplexen Bereich führt. Der andere ist der ausdrücklich geometrische Pfad, der über Entdeckungen wie die Verdoppelung von Quadrat und Würfel durch Archytas, Jacob Bernouillis Spira Mirabilis und Leibniz‘ Arbeiten über die Kettenlinie verläuft.[↩]
18. Eines der besten Beispiele hierfür ist die Entwicklung des Nationalstaatssystems im Gegensatz zur vorherigen feudalistischen Ordnung.[↩]
19. “Wendet man nämlich diese Abhängigkeitsgesetze in einem erweiterten Umfange an, indem man den veränderlichen Grössen, auf welche sie sich beziehen, complexe Werthe giebt, so tritt eine sonst versteckt bleibende Harmonie und Regelmässigkeit hervor.” (Bernhard Riemann, Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse, 1851).[↩]
20. Lyndon LaRouche, „Der wahre Staatsmann: Das historische Individuum“, Ibykus, 21. Jg., Nr. 81, 1.10.2002, Seite 4.[↩]