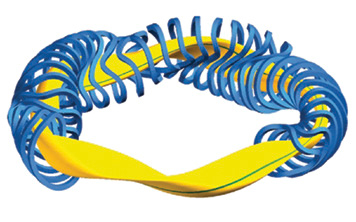
2017 ist Gauß-Jahr. Am 20. April wäre dieser große Mathematiker 240 Jahre alt geworden. Entgegen der Vorstellung, Gauß sei ein verknöchertes, verstaubtes Genie gewesen, wollen wir im folgenden zeigen, daß sein Denken höchst realitätsbezogen war, und er jeden etwas angeht. Er hat uns schließlich gezeigt, wie man vierdimensional denken kann. Ständig haben wir mit komplexen Flächen und Figuren zu tun, ohne uns dies bewußt zu machen – zum Beispiel das „Möbiusband“, genannt nach dem Gauß-Schüler Möbius, der nach Diskussionen mit Gauß auch noch andere komplexe Figuren wie Knoten aller Art oder den Gaußschen „Doppelring“ überliefert hat. Das Möbiusband (Abbildung 1), dieses geometrische Modell einer komplexen Funktion, benutzen wir heute ahnungslos als „Loop“ bzw. Strickschal im Winter (Abbildung 2). Auch Mechaniker verwenden solch ein Band oft als Antriebsriemen in riemengetriebenen Maschinen, und das Plasma im Fusionsreaktor Stellarator wird durch entsprechend geformte Feldspulen in eine möbiusbandförmige Bahn gebracht (Abbildung 3).

Das Möbiusband besitzt einen außerordentlichen physikalischen Nutzen, da man aufgrund seiner Geometrie beide Seiten benutzen kann (statt nur eine wie bei zylinderförmigen Bändern). Das sorgt bei Transmissionsriemen wie beim Plasma für eine gleichmäßige Abnutzung beider Seiten. Die Figur ist aber mathematisch sehr kompliziert und für einen Normalbürger schwer verständlich. Auch für Mathematiker war es lange Zeit schwer, sie durch eine mathematische Formel auszudrücken; erst im Jahre 2015 ist eine solche gefunden worden.1

„Loop“, ein einmal gedrehter
Strickschal, hat die Form
eines Möbiusbandes.
Und wer hätte das gedacht: Auch unsere leckere Laugenbrezel (Abbildung 4) ist in Wirklichkeit eine komplexe Konstruktion; sie ist ein Beispiel für eine dreifach zusammenhängende Riemannsche Fläche (Abbildung 5).
Allen diesen Figuren ist eines gemeinsam: sie besitzen eine völlig andere Geometrie als unsere normale, dreidimensional linearisch gedachte. Beim Möbiusband wird zum Beispiel eine in der linearen Ebene nicht zusammenhängende Strekke durch die Schaffung einer neuen Dimension zusammenhängend gemacht. Auf einem Zylinder mit einer Linie, die man innen oder außen zeichnet, kommt man niemals auf die andere Seite. Auf dem Möbiusband aber schon! Auch bei der Brezel hat man eine komplexe Geometrie, die im Gegensatz zu einer Kugel die Verbindung von Punkten ermöglicht, ohne daß sich die Linien schneiden, wie es zum Beispiel die Längen- und Breitengrade auf einer Kugel tun würden.
Diese komplexe Geometrie können wir uns weder linearisch noch dreidimensional vorstellen. Gauß dagegen hat – wie in seinem ganzen Werk deutlich wird – alle mathematischen Fragen geometrisch angepackt, und er hat mit der Schaffung der komplexen Ebene (Gaußsche Ebene) in gut verständlicher Weise eine höhere, komplexe Geometrie entwickelt, die eben solch mehrdimensionale Dinge geometrisch vorstellbar macht.

zusammenhängende Riemannsche Fläche.
Wer denkt bei öden algebraischen und komplexen Funktionen schon an die reale Welt? „Was soll‘s“, sagen die Mathematiker, „was habe ich mit der realen Welt zu schaffen?“ Das ist so wie bei den zwei Männern, die sich beim Ballonflug im Nebel verirrten. Im Dunst sahen sie einen weiteren Ballon und riefen ihm zu: „Bitte könnten Sie uns sagen, wo wir sind?“ Der Angesprochene ließ erst gar nichts von sich hören, und erst nach sehr langer Überlegung rief er zurück: „Sie sind im Korb eines Ballons!“ Die beiden sahen sich verblüfft an, und dann sagte der eine: „Das ist ein Mathematiker!“ „Wieso das denn?“, fragte der andere. „Ja, erstens hat er sehr lange nachgedacht, zweitens war seine Antwort hundertprozentig richtig, und drittens ist sie für uns hier vollkommen nutzlos.“
Tatsache ist: die Welt ist tatsächlich nicht so, wie sie scheint, aber sie ist viel interessanter, wenn man sie mit geometrischen Augen betrachtet. Es ist tatsächlich viel besser, man betrachtet Raum und Zeit von einer höheren geometrischen Warte, genau wie es uns Gauß gelehrt hat. Gauß hat die Kleinheit des Denkens, die in der Mathematik des 18. Jahrhunderts vorherrschte, revolutioniert, indem er wieder an das große Denken der Griechen und besonders an Archytas anknüpfte (auf den wir weiter unten noch zurückkommen werden). Er forderte von der mathematischen Welt den beständigen Bezug zur Anschauung, wie in einem Brief an seinen Freund, den Astronomen und Geodäten Heinrich Christian Schumacher, Gründer und Direktor der Sternwarte Altona (und Herausgeber der Astronomischen Nachrichten, 1780–1850), sehr klar wird:
„Es ist der Charakter der Mathematik der neueren Zeit (im Gegensatz gegen das Alterthum), daß durch unsere Zeichensprache und Namengebungen wir einen Hebel besitzen, wodurch die verwickelsten Argumentationen auf einen gewissen Mechanismus reducirt werden. An Reichthum hat dadurch die Wissenschaft unendlich gewonnen, an Schönheit und Solidität aber wie das Geschäft gewöhnlich betrieben wird, ebenso sehr verloren. Wie oft wird jener Hebel eben nur mechanisch angewandt, obgleich die Befugniß dazu in den meisten Fällen gewisse stillschweigende Voraussetzungen impliciert. Ich fordere, man soll bei allem Gebrauch des Calculs, bei allen Begriffsverwendungen sich immer der ursprünglichen Bedingungen bewußt bleiben, und alle Producte des Mechanismus niemals über die klare Befugniß hinaus als Eigenthum betrachten.“2
Das ist heute genauso aktuell wie vor 240 Jahren, als Gauß 1777 auf die Welt kam. Man kann auch sagen: Er fordert uns wirklich dazu auf, diese mehrdimensionale Verknüpfung in den Dingen zu sehen und nicht das „Scheinbare“ mit dem Wahren zu verwechseln. Er fordert uns auf, unsere Vorstellungskraft drastisch zu vergrößern. Nicht durch Drogen, sondern durch Überlegen, Nachdenken und Durchdenken geometrischer Probleme.
Beim Betrachten seiner geometrischen Herangehensweise werden wir sehen, daß Mathematik direkt mit dem lebendigen menschlichen Denkprozeß verknüpft ist, d. h. nicht einfach nur aus öden Formeln besteht, und daß es gar kein so großes Problem ist, vierdimensional oder gar noch mehrdimensionaler zu denken!
„Lebendig fühlen, was eigentlich fehlt“
„Daß das wirkliche Universum ganz anders ist als das scheinbare, ist eine Wahrheit, die nicht länger in Zweifel gezogen werden sollte.“ Mit diesen Worten beginnt Gauß‘ Lehrer Abraham Gotthelf Kästner (1719–1800) sein Vorwort zur ersten Veröffentlichung von Leibniz’ philosophischen Schriften im Jahre 1764. Er war ein Universalgelehrter und wirkte knapp 50 Jahre lang als Professor für Physik, Astronomie, Chemie, Botanik, Anatomie, Philosophie und Literatur in Göttingen. Genauso wie Gauß später war er Direktor der Sternwarte.
Kästner war für Gauß prägend; erstens stellte er eine direkte Verbindung zum Leibnizschen Denken dar, zweitens hatte er sich ausgiebig mit der viele tausend Jahre alten Geschichte der Mathematik befaßt und ein mehrbändiges Werk darüber herausgegeben. Er hat gesehen, daß die Mathematik die Entwicklung der Vorstellungskraft des Menschen zeigt und sie deshalb in einem ständigen Fortschreiten begriffen ist. Ihm war sehr bewußt, daß es dringend einer Änderung im festgefahrenen euklidischen Denken bedurfte, und verfaßte aus diesem Grunde gemeinsam mit seinem Schüler Georg Simon Klügel (1739–1812) eine kritische Schrift über die Euklidische Geometrie.
Der junge Gauß, der sich als Jugendlicher bereits durch die Bibliothek seines Landesherrn, Gönners und Förderers Herzog Karl Wilhelm Ferdinand „hindurchgelesen“ hatte, verstand dieses kritische Denken, das die bisherige dreidimensionale oder gar linearische Vorstellung der Geometrie von Punkten und Geraden angriff und auch vor der auf der Basis dieses dreidimensionalen Denkens basierenden Newtonschen Mechanik nicht Halt machte.
Die Idee einer neuen, antieuklidischen Denkweise packte Gauß, und er diskutierte darüber mit seinem ungarischen Freund Farkas (Wolfgang) Bolyai (1775–1856), der mit ihm zusammen in Göttingen studierte und später Professor für Mathematik, Physik und Chemie am Reformierten Kolleg in Marosvásárhely war. Hierdurch prägte sich seine sowieso schon hochentwickelte geometrische Auffassungsweise, bekennt er Jahre später in einem Brief an seinen Freund, den Astronomen Friedrich Wilhelm Bessel (1784–1846):
„… Auch über ein anderes Thema, das bei mir schon fast 40 Jahre alt ist, habe ich zuweilen in einzelnen freien Stunden wieder nachgedacht, ich meine die ersten Gründe der Geometrie: ich weiß nicht, ob ich mit Ihnen je über meine Ansichten darüber gesprochen habe. Auch hier habe ich manches noch weiter consolidiert, und meine Überzeugung, daß wir die Geometrie nicht vollständig a priori begründen können, ist, womöglich, noch fester geworden. Inzwischen werde ich wohl noch lange nicht dazu kommen, meine sehr ausgedehnten Untersuchungen darüber zur öffentlichen Bekanntmachung auszuarbeiten, und vielleicht wird dies auch bei meinen Lebzeiten nie geschehen, da ich das Geschrei der Böotier scheue, wenn ich meine Ansicht ganz aussprechen wollte.“
Mit den Böotiern waren die vom rückständigen Hegelschen System und dem allgemeinen „Anti-Leibnizschen“ Denken beherrschten Wissenschaftskreise vor allem in Berlin gemeint.
Wie sehr erinnert der allgemeine Geisteszustand dieser Zeit an heute. Damals hatten Leute wie Georg Wilhelm Friedrich Hegel (1770–1831) das Sagen, das Resultat war eine allgemeine Unwissenheit. Die Schulpflicht existierte zwar theoretisch, war aber wegen verbreiteter Kinderarbeit oft nicht realisiert.
Man muß sich dabei vorstellen, daß Hegels Habilitationsschrift von 1801 darin bestand, in typisch arroganter, besserwisserischer Manier zu „beweisen“, daß es nur sechs Planeten und vor allem zwischen Mars und Jupiter a priori keine weiteren Planeten mehr geben könne! Genau im selben Jahr hatte Piazzi aber den Planetoiden Ceres entdeckt, der allerdings nach drei Beobachtungen wegen widriger Umstände nicht mehr wiedergefunden wurde.
Gauß entwickelte daraufhin eine geometrische Methode zur Bestimmung der Bahnen von Himmelskörpern, mit der es ihm im Alter von 19 Jahren gelang, den Asteroiden Ceres „wiederzufinden“. Er war sich der Bedeutung seines Werkes völlig bewußt und sagte, daß es auch noch in Jahrhunderten studiert werden würde. Und tatsächlich wird bis heute genau diese Gaußsche Methode zur Bahnbestimmung benutzt.
Hegel aber wurde mit seiner Schrift nicht nur Professor an der Berliner Universität, er war von da an sogar federführend bei der Ernennung und Berufung von Mitarbeitern. Deshalb hat Gauß, obwohl er sich sein Leben lang mit der Entwicklung einer neuen Geometrie beschäftigte – ja praktisch alles, was er in Angriff nahm, geschah von einem höheren geometrischen Standpunkt –, seine wahren Ansichten nie an die große Glocke gehängt. Er schrieb frustriert über diese Situation in einem Brief an seinen Freund, den Arzt und Astronomen Friedrich Wilhelm Olbers (1758–1840):
„Die meisten Menschen haben gar nicht den rechten Sinn für das, worauf es dabei ankommt, und ich habe nur wenige Menschen gefunden, die das, was ich ihnen mitteilte, mit besonderem Interesse aufnahmen. Um das zu können, muß man erst recht lebendig gefühlt haben, was eigentlich fehlt, und darüber sind die meisten Menschen ganz unklar.“3
Und an Christian Ludwig Gerling (1788–1864), seinen langjährigen Mitarbeiter an der Göttinger Sternwarte, mit dem er über diese Ideen diskutierte, schrieb er schon 1818 zur Warnung über die ihm bevorstehenden Attacken:
„Ich freue mich, daß Sie den Mut haben, sich (in Ihrem Lehrbuch) so auszudrücken, als wenn Sie die Möglichkeit, daß unsere Parallelentheorie, mithin unsere ganze Geometrie falsch wäre, anerkennten. Aber die Wespen, deren Nest Sie aufstöbern, werden Ihnen um den Kopf fliegen.“4
Trotzdem hat er den Weg für diese neue Geometrie geebnet, die dann Bernhard Riemann und vor allem Einstein mit seiner Allgemeinen Relativitätstheorie (besser „Gravitationsgeometrie“) geschaffen haben.
Wie sehr Gauß an das Denken des Altertums und die polyphone geometrische Herangehensweise der Pythagoräer anknüpfte, zeigen Gespräche und Briefe, in denen Gauß die Unsterblichkeit der menschlichen Seele verteidigt, was zu dieser Zeit von der Lobby der Mechanisten, die im Menschen nur eine Maschine sahen, vehement abgestritten wurde. Gauß sagte in Gesprächen mit Rudolf Wagner (1805–1864), der diese Gespräche mit Carl Friedrich Gauß in den letzten Monaten seines Lebens, die von November 1854 bis zum 24. Dezember 1854 geführt wurden, aufschrieb (Gauß verstarb am 23. Februar 1855): „Ja! die Welt wäre ein Unsinn, die ganze Schöpfung ein Unding ohne Unsterblichkeit.“
Wagner berichtet auch, Gauß habe davon gesprochen, daß er bereits 1794, also mit 18 Jahren, ein Manuskript über die „Grundprinzipien der Philosophie der Mathematik“ geschrieben habe, das er aber nie veröffentlichte. Gauß sagte: „Das könne er bis auf den heutigen Tag als richtig unterschreiben“. Dieses Manuskript ist leider verlorengegangen, doch es war sicher aus dem Bedürfnis heraus verfaßt worden, etwas gegen die herrschende geisttötende und dekadente Denkkontrolle der damaligen Zeit zu setzen.
Geometrisches Denken statt „Formeln-Rechnen“
Wie hat Gauß erkannt, was der Wissenschaft „fehlte“? Und welche „Zauberkünste“ hat er angewendet, um uns die mehrdimensionale Welt geometrisch begreiflich zu machen? Gauß beherrschte, als er 1795 als Student nach Göttingen ging, schon mehrere Sprachen und besaß einen enormen Bildungsumfang. Zum Beispiel hatte er sich schon einen Namen gemacht durch die erfolgreiche, höchst ungewöhnliche geometrische Methode seiner Konstruktion des 17-Ecks, und man kann behaupten, daß er sich über den jämmerlichen Geisteszustand seiner wissenschaftlichen Umgebung völlig im Klaren war. Allein die Lösung dieses seit dem Altertum ungelösten Problems, welches von seinen Zeitgenossen schließlich für unlösbar erklärt worden war, zeigt dies deutlich.
Es war ganz offensichtlich: Seine geometrische Herangehensweise war revolutionär für die festgefahrene Mathematik der damaligen Zeit. All die großen Mathematiker konnten nichts anderes als rechnen, rechnen, rechnen. Die Algebra war seit der Einführung der arabischen Ziffern, die etwa seit dem 16. Jahrhundert allgemein bekannt wurden, mit der Zeit das Steckenpferd einer völlig neuen Kaste von „Rechenidioten“ geworden.

Was ist eigentlich Algebra? Ironischerweise hatte sie sich ursprünglich aus der Geometrie entwickelt! Über Tausende von Jahren hatte sich, vor allem bei den Ägyptern und dann insbesondere bei den Pythagoräern, ein hochentwickeltes geometrisches Verständnis über die Verhältnisse im Raum ausgebildet.
Die Babylonier kannten schon um 2000 v. Chr. geometrische Verhältnisse wie das Aufteilen von Flächen, die eine bestimmte Größe haben sollten, also Probleme wie:
x + y = a und xy = b ,
was ja bereits einer algebraischen Gleichung
x2 – ax + b = 0
entspricht, die sie durch Näherungen nur „ungefähr“ lösen konnten; auch hatten sie noch keinen Begriff von Inkommensurabilität oder sogenannten „irrationalen“ Verhältnissen, wie z.B. der Diagonale eines Quadrates. Derartige Verhältnisse haben die Ägypter dann aber mit geometrischen Methoden gelöst und dargestellt; bei Feldmessungen, Sternbeobachtungen oder dem Pyramidenbau ging es immer um reale geometrische Problemstellungen, die heute im allgemeinen Wust der „algebraischen Gleichungen“ untergehen.
Besonders die Griechen, die Schüler des Pythagoras, und hier vor allem Archytas, verstanden aber auch, daß alle Verhältnisse praktisch Abbilder einer höheren Geometrie sind, die nichts mit einem rein dreidimensionalen oder linearen Denken zu tun hat. Und genau dieses höhere geometrische Verständnis der Alten führte Gauß wieder in die Mathematik ein und schockierte so die geistig eingeschlafenen Algebraiker durch Geometrie. Wir werden diese Herangehensweise weiter unten an der höheren geometrischen Methode des Archytas von Tarent (ca. 435/410 bis ca. 355/350 v. Chr.), dem Freund Platons, kennenlernen, der schon komplexe Funktionen, wie sie Gauß später durch seine komplexe Ebene darstellbar machte, als miteinander verknüpfte Bewegung darstellte.
Imaginär, unmöglich oder was?
Mit gerade einmal 22 Jahren bewies Gauß – noch Student in Göttingen (Abbildung 6) – den sogenannten „Fundamentalsatz der Algebra“ und brachte hier ans Tageslicht, daß die bisherigen Beweise der großen Mathematiker des 17. und 18. Jahrhunderts wie D’Alembert, Euler/Poncelet und Lagrange nur Scheinbeweise und Selbstbetrug waren. Gauß zeigte, daß der berühmte Satz über die allgemeine Lösbarkeit von algebraischen Gleichungen beliebigen Grades – bei denen, wie jeder Schüler weiß, oft Lösungen als Wurzeln aus negativen Zahlen auftreten, die in der Mathematik lange als verboten galten – ohne ein vollkommen neues geometrisches Verständnis dieser algebraischen Gleichungen gar nicht bewiesen werden kann.
Die algebraische Rechenmethode stammte von dem arabischen Gelehrten Al Chwarizmi (um 780 bis nach 835 n. Chr.), der im „Haus der Weisheit“ am Hofe Harun al Raschids lehrte und in seiner Schrift von 825 al-Kitab al-Muchtasar fi hisab aldschabr wa-l-muqalaba – „Kurzes Buch über das Rechnen der Ergänzung und Ausgleichung“ – zeigte, wie man durch das Benutzen der sogenannten arabischen Ziffern 1, 2, 3, 4… geometrische Vorgänge praktischer ausdrücken konnte als mit den bis dahin üblichen römischen. Er wollte damit Rechnungen im Handel, bei rechtlichen Angelegenheiten oder bei der Landvermessung einfacher gestalten, und heute ist diese Methode aus keiner Wissenschaft mehr wegzudenken.
Aber wie Gauß schon bemerkte, mit der Zeit blieb die geometrische Vorstellung in der Mathematik aus geistiger Bequemlichkeit auf der Strecke. Und wie das immer so ist, wenn man Schein und Wirklichkeit verwechselt, tauchten sehr bald unüberwindliche Paradoxe auf. So stieß man bei manchen „normalen“ quadratischen Gleichungen auf unlösbare Probleme, wie zum Beispiel bei der Lösung der algebraischen Gleichung
x2 + 3 = 0 ==> x = √– 3 .
Das war völlig unverständlich! Wie soll man sich eine negative Fläche vorstellen? Aber da den Mathematiker die reale Welt nicht interessiert, geht er gedankenlos und ohne jedes Verständnis einer geometrischen Vorstellung durch die Welt und sagt: „Paßt mal auf: Wir wollen doch weiterrechnen können. Deswegen denken wir uns etwas aus, auch wenn wir alle wissen, daß es das gar nicht gibt: etwas Imaginäres.“ Und so definierte man eine neue imaginäre Zahl als:
i2 = – 1 ,
mit der die obige Gleichung eine Lösung bekommt, nämlich: x = i √3
Dieses Paradox beschäftigte Gauß sein Leben lang immer wieder; man erkennt das daran, daß er den sog. Fundamentalsatz der Algebra in 50 Jahren viermal immer wieder neu und genauer bewies. In diesen Beweisen schuf er seine neue Geometrie: Zuerst bewies er den Satz strikt ohne die imaginäre Zahl, entwickelte aber in den folgenden Jahren ein klares Verständnis über eine wirkliche geometrische Begründung einer ganz neuen Art von Zahlen, mit denen er eine vierdimensionale Geometrie schuf und uns das Handwerkszeug zum Verständnis von mehrdimensionaler, mehrfach verknüpfter Bewegung lieferte.
Seine erste Beweisschrift beginnt Gauß damit, die bisherigen sogenannten „Beweise“ der großen Mathematiker genüßlich auseinanderzunehmen und zeigt deren allgemeine Mangelhaftigkeit auf:
„Das bisher Besprochene wird in den Lehrbüchern der Algebra auf ausreichende Weise bewiesen; es verstößt auch nirgends gegen die mathematische Strenge.
Doch scheint es, als ob die Analytiker etwas zu übereilt und ohne vorausgehenden gründlichen Beweis denjenigen Lehrsatz aufgenommen hätten, auf welchem sich fast die gesamte Lehre von den Gleichungen aufbaut,
daß nämlich eine jede solche Funktion wie X
(xm + Axm – 1 + Bxm – 2 + … + M = 0, wobei m eine ganze positive Zahl ist)
stets in m lineare Faktoren zerlegt werden könne, oder, was hiermit völlig übereinstimmt, daß jede Gleichung m’ten Grades wirklich m Wurzeln besitze. [Das Wort „Wurzel“ ist hier als „Lösung“ zu verstehen, Anm. Red.]
Da man bereits bei den Gleichungen zweiten Grades sehr häufig auf solche Fälle stieß, welche diesem Satze widersprachen, so waren die Algebraiker gezwungen, um jene Fälle diesem Theorem unterordnen zu können, eine gewisse imaginäre Größe zu ersinnen, deren Quadrat – 1 ist; dann erkannten sie, daß, wenn Größen von der Form a + b √– 1 ebenso wie reelle zugelassen werden, der Lehrsatz nicht allein für Gleichungen zweiten Grades wahr sei, sondern auch für cubische und biquadratische…;
Es bildet das Ziel der vorliegenden Abhandlung, einen neuen, strengen Beweis desselben zu geben.“5
Weiter sagt er über die Willkür dieser von den Algebraikern unverstandenen Art von Größen:
„Übrigens wurden in jener Zeit, in welcher die Analytiker erkannten, es gäbe unendlich viele Gleichungen, die überhaupt nur Wurzeln besitzen, wenn Größen der Form a + b √– 1 zugelassen werden, derartig erdachte Größen als eine ganz besondere Größenart, welche man zum Unterschied von den reellen Größen imaginär nannte, betrachtet und in die gesamte Analysis eingeführt.
Mit welchem Recht dies geschehen sei, will ich hier nicht erörtern…
Wenngleich dasjenige, was in den meisten elementaren Schriften als Beweis unseres Lehrsatzes angeführt wird, so haltlos und so wenig streng erscheint, daß es kaum der Erwähnung werth ist, so will ich doch, um keine Lücke zu lassen, mit wenigen Worten darauf eingehen.“
Und weiter:
„Einige Schriftsteller, welche wohl die Schwäche dieser Methode erkannt haben mögen, nehmen es gewissermaßen als Axiom an, daß jede Gleichung wirklich, wenn keine möglichen, so doch unmögliche Wurzeln besitze. Was sie unter möglichen oder unmöglichen Größen verstanden wissen wollen, haben sie wohl nicht klar genug auseinandergesetzt: ,Obgleich wir noch nicht sicher sind, daß es nothwendig m reelle oder imaginäre Größen gibt, welche irgendeiner gegebener Gleichung m’ten Grades genügen, so wollen wir dies doch zunächst annehmen; denn sollte es sich treffen, daß nicht so viele reelle und imaginäre Größen gefunden werden können, dann bleibt uns ja der Ausweg offen, zu sagen, die übrigen seien unmöglich.’.“
Und dann schiebt er humoristisch ein:
„Wenn Jemand sagt, ein geradliniges, gleichseitiges, rechtwinkliges Dreieck sei unmöglich, so wird dem Niemand widersprechen. Will man dagegen ein solches unmögliches Dreieck als eine neue Dreiecksart betrachten und andere Dreieckseigenschaften auf dieses anwenden, so wird Jeder dies lächerlich finden! Das heißt mit Worten spielen oder vielmehr Mißbrauch treiben.“
Und weiter über Eulers sogenannten „Beweis“, der dafür außer den imaginären noch die erwähnten „unmöglichen“ Zahlen eingeführt hatte:
„Da man sich aber außer reellen und imaginären Größen a + b √– 1 keine anderen Größen-Formen vorstellen kann, so ist es nicht ganz klar, worin sich das, was bewiesen werden soll, von dem unterscheidet, was als Grundsatz angenommen wird; … Wie aber solche Größen, über die wir uns nicht einmal eine Vorstellung bilden können – wahre Schatten von Schatten – summiert oder multipliziert werden sollen, das läßt sich bei der in der Mathematik stets geforderten Klarheit nicht verstehen.“
Für diese Arbeit, die der 22jährige in lateinischer Sprache verfaßt hatte, erhielt er von der Universität Helmstedt 1799 in Abwesenheit und ohne mündliche Prüfung den Doktortitel.
Gauß bewies diesen algebraischen Satz 50 Jahre später in einer klaren und durch und durch neu formulierten Geometrie, was keiner hinter den trockenen algebraischen Formeln vermutet hätte. Und er war sich seiner Revolution des bisherigen mechanischen Denkens der Mathematik voll bewußt.
Das Theatergespenst Vierdimensionalität
Ein Beispiel aus Gauß’ Schulzeit zeigt, daß er in seinem Denken praktisch von Kindheit an die Geometrie der Zahlen sah und nicht nur das „Zeichen“, das sie darstellt. Der Lehrer hatte den neunjährigen Kindern einmal die Aufgabe gestellt, nur mit Schiefertafel und Kreide die Zahlen von 1 bis 100 zusammenzuzählen. Während alle Schüler die ganze Stunde mühsam und meist erfolglos Zahlen zusammenzählten, meldete sich der kleine Gauß nach ein paar Minuten, legte seine Tafel dem Lehrer vorne aufs Pult mit den Worten: „Liggetse.“ Der Lehrer hielt das für äußerst vorwitzig und hatte sich schon eine Tracht Prügel für den Bengel vorgenommen, war aber höchst erstaunt, als er auf der Tafel die richtige Zahl 5050 las. Ärgerlich einen Schwindel ahnend rief er den Kleinen auf: „Gauß! Nach vorne kommen – heraus mit der Sprache! Wie ist er zu diesem Resultat gelangt?“ Gauß antwortete: „Im Kopf ausgerechnet, Herr Lehrer. Für eine so einfache Aufgabe brauche ich Tafel und Griffel nicht!“ Und dem sprachlosen Lehrer erklärte der Knirps weiter:
„Nun, ich habe mir überlegt, daß die erste Zahl 1 und die letzte Zahl 100 zusammen 101 ergeben. Das Gleiche gilt für 2 und 99, 3 und 98, und so weiter. Das sind also 50 Zahlenpaare; fünfzig mal 101 ergibt aber 5050!“
Was haben Zahlen mit Geometrie zu tun? Mathematik gilt gemeinhin als knochentrockene Sache, die nichts mit unserer Welt, also den drei Dimensionen, in denen wir leben, zu tun hat. Ganz im Gegenteil, sie hat sehr viel mit unserer wahren Welt zu tun, nur ist diese Welt eben nicht nur dreidimensional und viel faszinierender, als wir uns sie vorstellen.
Es geht nicht darum, komplizierte Zahlen zu bestaunen und ihre Mystik zu ergründen, wie das vielen bei der Betrachtung der Konstanten π oder der Primzahlen passiert, sondern um die Vorstellungskraft des menschlichen Geistes, die die „Bewegung“ hinter den Zahlen sieht, oder wie Gauß sagt:
„daß die logischen Hilfsmittel für sich nichts zu leisten vermögen und nur taube Blüten treiben, wenn nicht die befruchtende lebendige Anschauung des Gegenstandes darüber waltet.“6
Beim „Denken“ an Zahlen hat man eigentlich immer eine Geometrie im Kopf. Bei den ganzen Zahlen denken wir unwillkürlich an vorwärts und rückwärts und oben und unten, bei den rationalen Zahlen, also Brüchen, denken wir an Teile eine ganzen Apfels, die Hälfte, ein Viertel etc.. Wenn wir aber eine ganze Stunde in Brüche, also rationale Zahlen, aufteilen wollen, gelangt man schnell zum Paradox der Inkommensurabilität, denn die Bruchteile lassen sich irgendwann nicht mehr als rationale Verhältnisse eines Ganzen darstellen. Eine Viertelstunde sind noch 0,25 Stunden, doch bei 10 Minuten, was 1/6 einer Stunde ausmacht, wird es schwierig – wieviel ist das als Dezimalzahl? Das Problem entsteht dadurch, daß man die Stunde in 60 Minuten aufteilen kann oder in 100 Teile, aber die 100 und die 60 sind nicht völlig ineinander aufteilbar.
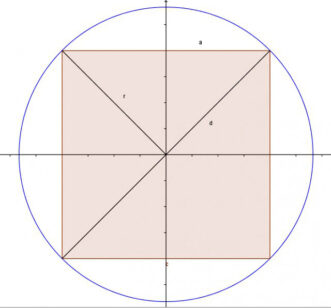
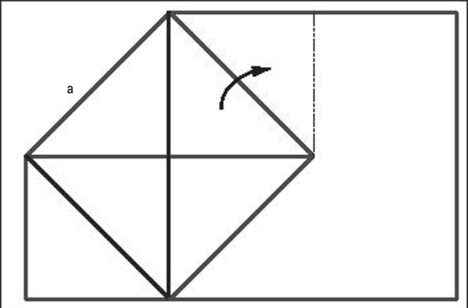
Will man ein Quadrat verdoppeln, sieht man das Paradox geometrisch vor Augen. Die Seite des neuen, verdoppelten Quadrats ergibt sich, wenn man die Diagonale, die das Quadrat in vier Teile geteilt hatte, nach außen dreht. Algebraisch handelt es sich hier darum, die Gleichung
x2 – 2 = 0
zu lösen, d. h. wenn wir die Seite des Ausgangsquadrats a = 1 setzen, so fragen wir, wie groß die Seite x des verdoppelten Quadrats sein muß, dessen Fläche x2 = 2 ist. (siehe Abbildungen 7 a, 7 b)
Diese Zahlen hatten bis jetzt noch irgendwie Platz in unserem dreidimensionalen Denken. Wie würden wir uns aber mehr Dimensionen vorstellen, wie es Gauß entwickelt hat? Diese von Gauß entwickelte sogenannte „Komplexe Gaußsche Ebene“ hatte Einstein später sogar zur Grundlage seiner Allgemeinen Relativitätstheorie gemacht, mit den Worten:
„Ein mystischer Schauer ergreift den Nichtmathematiker, wenn er von ,vierdimensional’ hört, ein Gefühl, das dem vom Theatergespenst erzeugten nicht unähnlich ist. Und doch ist keine Aussage banaler als die, daß unsere gewohnte Welt ein vierdimensionales zeiträumliches Kontinuum ist.“7
Gauß selber beschreibt seine neue Geometrie dann nach 50jähriger Beschäftigung mit dem geometrischen Hintergrund der Algebraischen Gleichungen in seinem vierten Beweis des Fundamentalsatzes, den er 1849 veröffentlichte. Hier läßt er erkennen, welch ganz andere Konzeption des Raumes ihm dabei vorschwebt:
„Ich werde die Beweisführung in einer der Geometrie der Lage entnommenen Einkleidung darstellen, weil jene dadurch die größte Anschaulichkeit und Einfachheit gewinnt. Im Grunde gehört aber der eigentliche Inhalt der ganzen Argumentation einem höheren, von Räumlichem unabhängigen Gebiete der allgemeinen abstrakten Größenlehre an, dessen Gegenstand die nach der Stetigkeit zusammenhängenden Größenkombinationen sind, einem Gebiete, welches zur Zeit noch wenig angebaut ist, und in welchem man sich auch nicht bewegen kann ohne eine von räumlichen Bildern entlehnte Sprache.“8
Um seine staunenswerte Idee wenigstens ansatzweise zu verstehen, betrachten wir kurz die Konstruktion der komplexen Ebene, und wie sich Zahlen und Funktionen darin darstellen. Bisher war es ja so, daß man sich ohne weiteres eine algebraische Gleichung zumindest bis zum dritten Grad vorstellen konnte: a2 ist zum Beispiel ein Quadrat, bei a2 + b2 denkt man an den Satz des Pythagoras für Dreiecksverhältnisse, 3a2 wären drei Quadrate nebeneinander, und bei a3 haben wir einen Würfel. Bei a4 wäre dann die Grenze unserer Vorstellungskraft erreicht. Und was soll dann a + b √– 1 oder a + b · i bedeuten? An diesem Punkt führt Gauß die komplexe Ebene ein, die zwar Ebene heißt, aber in Wirklichkeit einen vierdimensionalen Raum darstellt. Damit macht uns das a4 schon einmal keine Probleme mehr.
Gauß entwickelt in seinem vierten Beweis das System der komplexen Ebene, indem er von Anfang an algebraische Gleichungen als komplex darstellt. Er betrachtet eine übliche algebraische Gleichung der Form
X = xn + Axn – 1 + Bxn – 2 + … Mx + N .
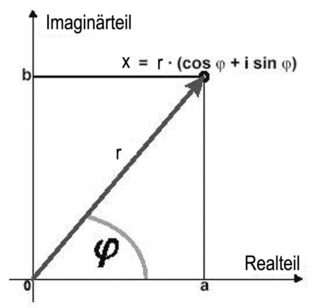
Doch er sagt von vornherein, da wir sowieso auch komplexe Zahlen immer als Lösung annehmen, ersetzen wir von Anfang an das x, das man normalerweise als natürliche Zahl sieht, durch jeweils die komplexe Zahl x = t + i · u, wobei i immer die imaginäre Einheit i = √– 1 sein soll – ein erster wichtiger Schritt. Das x = t + i · u sind aber „Zahlen“, die man in der komplexen Ebene darstellen muß, d. h. sie sind nicht in der linearen Achse darstellbar, sondern in einer Ebene, bei der die übliche x-Achse die Werte von t, die y-Achse die von i · u darstellen.
Als nächstes zeigt Gauß, daß man sich diese Ebene ebenso als Kreisebene vorstellen kann, und daß die Positionen dieser „Zahlen“ auch im Dreieck durch Cosinus und Sinus darstellbar sind, die sogenannten „Polarkoordinaten“. Dann wird aus der gleichen Zahl x
x = r cos φ + i · r sin φ (siehe Abbildung 8).
Dabei ist r immer die Entfernung vom Mittelpunkt zum Punkt x, und φ der Winkel, der seine Lage durch die Benutzung der Sinus- und Cosinus-Beziehung im Dreieck beschreibt. Gauß betrachtet nun beide Teile dieser Zahlen getrennt: r cos φ nennt er den Realteil T(x) von x, und i · r sin φ den Imaginärteil i · U (x) von x.
Die Zahl heißt dann also bei Gauß: x = T (x) + i · U (x).
Eine algebraische Funktion siebten Grades – d. h. eine siebendimensionale Gleichung –, die anfangs so aussieht:
F(x) = x7
wird in Gauß’ Darstellung der komplexen Ebene (mit x = r cos φ + i · r sin φ) und mit dem Gesetz zur Multiplikation der komplexen Zahlen verwandelt in:
F(x) = |x| · cos 7φ + i · |x| · sin 7φ
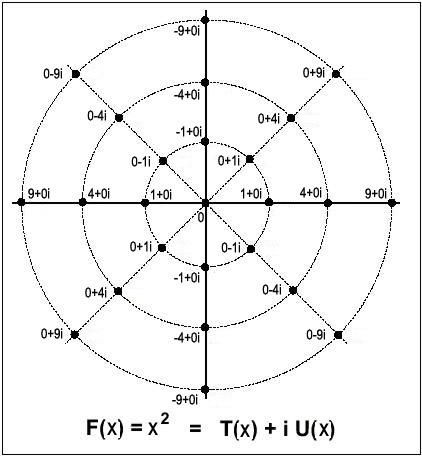
Gauß betrachtet nun getrennt die Realteile und Imaginärteile der Funktionen und ihr Verhalten im gesamten Kreis, indem er für φ alle Werte von 0 bis 360° einsetzt. So zeigt er schließlich auf sehr einsichtige Weise, daß es eine Lösung für algebraische Gleichungen nur dann gibt, wenn die Real- und Imaginärteile der Funktion gemeinsame Nullstellen besitzen, womit er den Fundamentalsatz beweisen kann, nämlich daß alle algebraischen Gleichungen immer genauso viele Lösungen haben müssen, wie der Grad ihrer Dimension ist; eine Gleichung siebten Grades hat somit sieben gemeinsame Nullstellen ihrer Real- und Imaginärteile, eine Gleichung zweiten Grades nur zwei.
Um sich das zu verdeutlichen, sollte der Leser selbst einige Funktionen ausrechnen. Man kann sich, wenn man eine Funktion selbst im Kreis aufzeichnet (Abbildung 9), diese schöne Regelmäßigkeit klarmachen, denn diese kommt von der regelmäßigen Bewegung von Sinus und Cosinus, deren Phasen um 90° verschoben sind, deren Werte aber im Kreis bei fortlaufender Umdrehung immer wieder gleiche Werte annehmen; z.B. ist der Sinus bei 0°, 180° und 360° gleich 0, der Cosinus bei 90° und 270° gleich 0. Als Beispiel sehen wir sehr schön an der bildlichen Darstellung der Funktion z2, wie die Nullstellen von Real- und Imaginärteil mit der Cosinus- und Sinusfunktion zusammenhängen (Abbildung 10).

Die öden algebraischen Formeln werden hier zu Gebilden im Raum, die durch miteinander verknüpfte Bewegungen zustande kommen. Wir erahnen nun, daß Gauß‘ geometrische Methode ein durchschlagend anderes Denken in die Algebra einführte.
Würfelverdoppelung zur Lösung von Krisen
Daß diese neue Herangehensweise notwendig für die heutige Krise ist, zeigt ein hervorragendes Beispiel der Antike: das Problem der Verdoppelung des Würfels. Immer, wenn man politisch in einer tiefen Krise steckte, wurde von den Weisen angeordnet, daß man sich mit vereinten Kräften daranmachen solle, den Würfel zu verdoppeln, um so auch die Krise zu lösen!
Man bedenke, daß es sich hier bereits um eine algebraische Gleichung dritten Grades handelt, wenn der anfängliche Inhalt des Würfels gleich 1 angenommen wird. Die gesuchte Seite x des verdoppelten Würfels mit dem Inhalt 2 findet man dann durch die Gleichung:
x3 = 2 oder x3 – 2 = 0
Dieses sogenannte „Delische Problem“ stellte die alten Geometer vor Probleme. Moritz Cantor berichtet in seiner Geschichte der Mathematik von 1880 (S. 181) über einen Brief von Eratosthenes an den ägyptischen König Ptolemäus:
„Dem Könige Ptolemäus wünscht Eratosthenes Glück und Wohlergehen. Von den alten Tragödiendichtern [Anm.: gemeint ist Euripides mit seinem verloren gegangenen Werk Poleidos] sagt man, habe einer den Minos, wie er dem Glaukos ein Grabmal errichten ließ, und hörte, daß es auf allen Seiten 100 Fuß haben werde, sagen lassen:
Zu klein entwarfst Du mir die königliche Gruft, Verdopple sie; des Würfels doch verfehle nicht.
Man untersuchte aber auch von Seiten der Geometer, auf welche Weise man einen gegebenen Körper, ohne daß er seine Gestalt veränderte, verdoppeln könnte, und nannte die Aufgabe der Art des Würfels Verdoppelung; denn einen Würfel zugrunde legend suchte man diesen zu verdoppeln. Während nun lange Zeit hindurch Alle ratlos waren, entdeckte zuerst… Hippokrates, daß, wenn man herausbrächte zu zwei gegebenen geraden Linien, wovon die größere der kleineren Doppelte wäre, zwei mittlere Proportionalen von stetigem Verhältnisse zu ziehen, der Würfel verdoppelt werden könnte; wonach er dann seine Rathlosigkeit in eine nicht geringere Rathlosigkeit verwandelte.
Nach der Zeit, erzählt man, wären die Delier, weil sie von Krankheit befallen waren, einem Orakel zufolge geheißen worden einen ihrer Altäre zu verdoppeln und in dieselbe Verlegenheit gerathen. Sie hätten aber die bei Platon in der Akademie gebildeten Geometer beschickt und gewünscht, sie möchten ihnen das Verlangte auffinden. Da sich nun diese mit Eifer der Sache unterzogen und zu zwei Gegebenen zwei Mittlere suchten, soll sie … Archytas vermittels der Halbzylinder aufgefunden haben…“
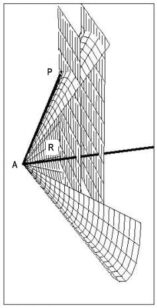
Wir wollen die Problemlösung des Archytas hier näher betrachten, denn seine Konstruktion, die Auffindung der Seite des neuen, verdoppelten Würfels als einen durch drei Bewegungen erzeugten Prozeß im Raume – der Schnittpunkt der Flächen eines Zylinders und eines Kegels mit der Kugelsphäre, in deren Mittelpunkt der Anfangspunkt der gesuchten Strecke liegt, ist die eindeutige Lösung – entspricht genau der Gaußschen Konstruktion zur Lösung des Fundamentalsatzes der Algebra: auch hier werden die Lösungen einer Gleichung als die Schnittpunkte der aus jeweils dem Realteil und Imaginärteil der trigonometrischen Kurven erhaltenen Kurven gefunden. Man kann fast annehmen, daß Gauß die Herangehensweise des Archytas gekannt hat, bei dem wir bereits das komplexe geometrische Denken finden, mit dem Gauß die Mathematik aus ihrer Sackgasse herausgeholt hat.
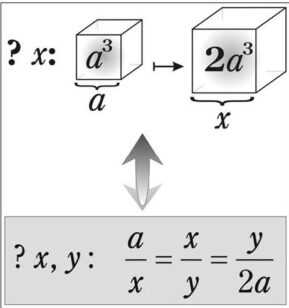
Die Lösung baut auf der bei Erathosthenes erwähnten grundlegenden Überlegung des Hippokrates von Chios auf, daß die zwei mittleren geometrischen Mittel, also zwei Größen X und Y zwischen zwei gegebenen Größen a und b aufgefunden werden müssen (wobei b größer sein soll als a), so daß:
a : X = X : Y = Y : b
Um das zu erklären, betrachte man hier den Sonderfall a = 1 und b = 2. a ist hier der Inhalt des Ausgangswürfels, b der genau verdoppelte Inhalt des gesuchten Würfels. Das erste der beiden geometrischen Mittel, X, entspricht der Seite eines Würfels mit der doppelten Fläche des Ausgangswürfels. Das zweite Mittel, Y, entspricht der Fläche einer Seite des neuen Würfels. Bei dem Verdoppelungsprozeß geht man dann in drei Schritten vor: Zuerst zieht man den Würfel mit der Seitenlänge 1 so in die Breite, daß seine eine Seitenlänge gleich X wird, also die Größe des verdoppelten Würfels annimmt, d. h. sein Volumen vergrößert sich zu
1 ∙ 1 ∙ X .
Anschließend streckt man ihn nach hinten in die Tiefe, wodurch Breite und Tiefe bereits die gesuchte Länge X erreichen. Der Inhalt ist
X ∙ X ∙ 1 .
Dann zieht man ihn noch in die Höhe, so daß sich der doppelte Würfel mit der Seitenlänge X ergibt, d. h.
X3 = 2 .
Die Seitenlänge X des Doppelwürfels ist also die erste der zwei mittleren Proportionalen zwischen 1 und 2 (Abbildung 11).
Die große Ratlosigkeit des Hippokrates verwandelte sich bei diesem ersten, sehr wichtigen Grundgedanken aber nur in eine noch größere Ratlosigkeit. Denn es läuft immer wieder aufs gleiche hinaus: die algebraischen Gleichungen sind nur verstehbar durch eine höhere Geometrie polyphoner, also miteinander verknüpfter Bewegungen. Und das zeigte Archytas.
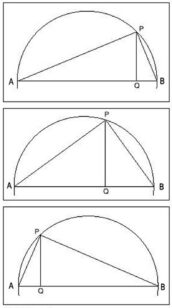
Um nun Archytas’ Konstruktion der drei zusammenhängenden Bewegungen von Zylinder, Kegel und Halbkreis (Abbildung 12) zu verstehen, erinnern wir uns an die Proportionen, die in einem Kreis gelten. Von Pythagoras wissen wir nämlich, wenn wir über einem Durchmesser AB einen Halbkreis schlagen und das Dreieck durch die Verbindung von A, B und einem Punkt P auf dem Kreis bilden, so ergeben sich kontinuierlich harmonische Proportionen; man kann so unendlich viele Dreiecke erzeugen, indem man einfach mit dem Punkt P auf dem Halbkreis weiterwandert (Abbildung 13).
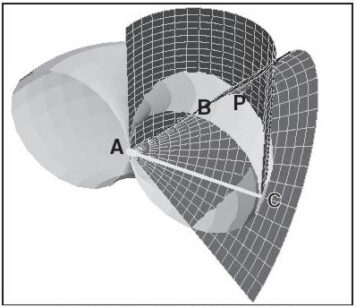
Der Winkel APB bleibt immer einer rechter. Wir haben also unendlich viele rechtwinklige Dreiecke. Wenn wir nun von P eine Linie auf den Durchmesser projizieren und diesen Punkt Q nennen, so erhalten wir wiederum ein rechtwinkliges Dreieck, das dem ersten ähnlich ist, weil es bei A mit dem ersten einen gemeinsamen Winkel besitzt. Wenn wir mit P wieder auf dem Halbkreis wandern, so werden die beiden Dreiecke APB und APQ trotzdem immer ähnlich bleiben und es gelten die Verhältnisse
AQ : AP = AP : AB .
Das heißt aber nichts anderes, als daß die Länge AP das geometrische Mittel zwischen AQ und AB darstellt.
Für die Würfelverdoppelung brauchten wir aber laut Hippokrates zwei mittlere Proportionale zwischen dem Inhalt 1 und dem des verdoppelten Würfels 2, d. h. wir brauchen so etwas wie:
1 : AQ = AQ : AP = AP : 2
Wenn wir jetzt einen Kreis mit dem Durchmesser AB = 2 nehmen und die gleiche Konstruktion wie eben ausführen, so haben wir schon den ersten Teil dieser Operation:
AQ : AP = AP : 2
Wie erhalten wir jetzt die zweite Proportion? Man könnte einen zweiten Kreis um die Strecke AP als Durchmesser des zweiten Kreises konstruieren. Wenn wir nun den Punkt Q auf den neuen Durchmesser im Punkt O projizieren, muß die Strecke AO die Länge 1 haben, denn dann erhalten wir wie beim ersten Kreis die Beziehung zwischen ähnlichen Dreiecken:
1 : AQ = AQ : AP
Wir sehen jetzt einen mehrfach verknüpften Prozeß, wenn wir P auf dem ersten Halbkreis entlangwandern lassen: dadurch erzeugen wir kontinuierlich neue Kreise, der Durchmesser AP ändert sich dabei stetig, die Verhältnisse unter den Dreiecken bleiben aber gleich (Abbildung 14).
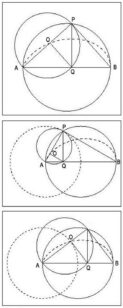
Wenn man es recht bedenkt, dann haben wir uns hier aber selbst ausgetrickst: Wir bezeichneten die Strecke AO bereits als 1, ohne aber zu wissen, ob das überhaupt stimmt. Erst, wenn das wirklich der Fall ist, d. h. wenn wir wirklich den Kreis auf AP finden mit der Strecke AO = 1, ist die Bedingung der zwei mittleren Proportionen erfüllt. Dann erst gilt:
1 : AQ = AQ : AP = AP : 2
Anders ausgedrückt: dann erst ist die Seite des verdoppelten Würfels bekannt, die ja laut Hippokrates’ Überlegungen x = AQ ist – die erste der zwei mittleren Proportionen.
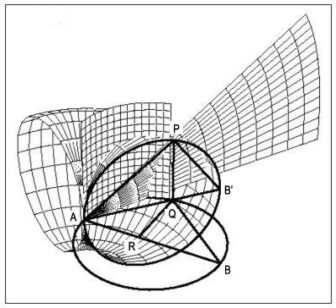
Wenn wir uns nun die Konstruktion noch einmal anschauen und den Punkt O betrachten, so sehen wir, daß er ebenfalls einen Kreis beschreibt, wenn P auf dem Kreisumfang des ersten Kreises entlangwandert (Abbildung 15). Wir werden also bei dieser dritten Bewegung nur in die richtige Position gelangen, wenn wir um den Punkt A einen Kreis mit Radius 1 schlagen: jetzt sehen wir, wie diese mehrfach verknüpfte Bewegung genau den Punkt O erzeugt, den wir für die Vervollständigung unserer Proportionen brauchen.
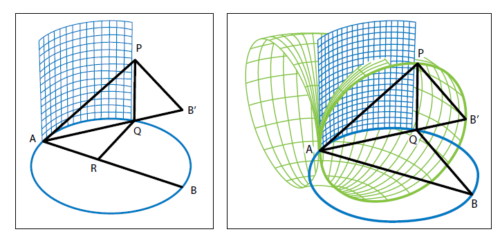
Dies ist im Ansatz schon die Idee des Lösungsweges des Archytas, der auch durch eine dreifach verknüpfte Bewegung den richtigen Punkt für die Bedingungen des Hippokrates für die zwei mittleren Proportionen erzeugt. Er hat aber eindeutig einen höheren geometrischen Hintergedanken: Er erzeugt diesen gesuchten Punkt durch die Verknüpfung dreier verschiedener geometrischer Körperbewegungen, durch drei verschiedene Geometrien. Und das zeigt, daß er ähnlich vorgeht wie Gauß mit seiner Darstellung der algebraischen Formeln als Verknüpfung zweier unabhängig bewegter trigonometrischer Funktionen, wobei die eine den Realteil, die andere den Imaginärteil der Gleichung darstellt.
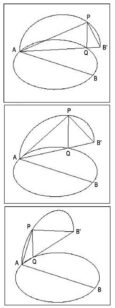
Archytas konstruiert wieder den Ausgangskreis mit dem Durchmesser AB = 2, errichtet aber auf diesem AB senkrecht stehenden gleichen Kreis einen zweiten mit Durchmesser AB, den er durch die senkrechte Achse bei A vertikal schwenkt (Abbildung 16). Mit diesem senkrechten Kreis auf AB wird ein Torus mit der mittleren Achse bei A und eben dem Durchmesser AB erzeugt. Nun erzeugt Archytas die zweite geometrische Figur, nämlich einen Zylinder mit dem Durchmesser AQ. Q ist ja der Punkt, bei dem P auf die ursprüngliche Ebene des Kreises um AB projiziert wird. Wir können diese zweifach verknüpfte Bewegung einmal genauer betrachten, um uns klarzumachen, daß hier genau die gleichen Beziehungen wie bei der Konstruktion in der Ebene gelten. Wenn wir nun den Punkt P auf dem senkrechten Kreisbogen (der Oberfläche des Torus) bewegen, so erhalten wir wieder eine kontinuierliche große Anzahl von verschiedenen Zylindern, die zwar immer einen unterschiedlichen Durchmesser AQ haben, in denen aber immer die gleiche Beziehung zwischen ähnlichen Dreiecken gilt:
AQ : AP = AP : 2 (weil ja AB = 2 sein sollte)
Um nun aber wieder die zweite Proportion zu erhalten, so daß wir die richtige Seite des verdoppelten Würfels erzeugen können, müssen wir, ähnlich wie eben, noch eine dritte Geometrie einführen. Betrachten wir wieder (Abbildung 17) die Projektion von Q auf die Strecke AP im Punkt O. Wir sehen, daß die Bewegung von P auf dem Torusbogen erstens eine Bewegung von Q auf dem Durchmesser des Torus AB erzeugt, daß aber auch O sich wieder in einem Bogen bewegt. Was ist das für ein Bogen, der durch die Bewegung erzeugt wird?
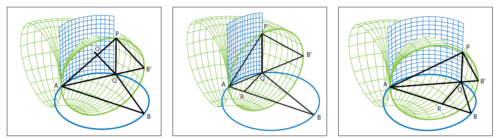
erzeugt, daß aber auch O sich in einem Bogen bewegt.
Dafür betrachten wir die Strecke QO genauer: Es ist ja die gleiche Strecke wie die, die wir erhalten, wenn wir Q in dem ursprünglichen waagerechten Kreis auf dem Durchmesser AB abbilden. Wir nennen diesen Punkt R. Das muß sich sehr gut vorstellen: Punkt P kann ja nicht nur (wie gesagt, bei gleichbleibenden ähnlichen Verhältnissen) auf diesem einen senkrechten Torusbogen wandern, sondern der Kreisbogen APB kann auch nach vorne und hinten bzw. einmal ganz herum auf dem Torusbogen „kippen“, praktisch wie auf einem Kreisbogen des Torus, der auf der waagerechten Schnittebene immer den Durchmesser AB hat. Dabei haben die Punkte R oder O (bzw. noch viel mehr durch diese erzeugten Kreise in verschiedenem Abstand von A) alle den gleichen Abstand von A und erzeugen einen neuen Kreis. Dieser Kreis hat – von A aus betrachtet – einen ständig wachsenden Radius AR bzw. AO etc. Das Gebilde, das hier erzeugt wird, ist eine dritte, neue Geometrie, nämlich ein Kegel (Abbildung 18).
Die Achse des Kegels stellt jetzt sozusagen eine Proportionalitätsachse dar und muß bis zu einem genau bestimmten Öffnungsgrad des Kegels reichen. Betrachten wir nun die Proportionen, denn Archytas hat auch hier eine absolut genaue Lösung gezeigt, die nicht, so wie in der Ebene, Spielraum ließ für die freie Wahl des Radius um A, der die Länge 1 haben soll. Es gilt, wie wir gesehen haben:
AR : AQ = AQ : 2
d. h. auch das umgekehrte
2 : AQ = AQ : AR .
Genauso hatten wir gesagt, muß gelten:
1 : AQ = AQ : AP ,
damit wir die beiden gewünschten mittleren Proportionen bekommen. An diesen beiden Beziehungen sehen wir, daß der Faktor, der 1 zur mittleren Proportion bringt, genau doppelt so groß ist wie der Faktor, der 2 in AQ transformiert. Daraus können wir das Verhältnis ableiten:
1 : AQ = AQ : (2 · AR)
Um das gewünschte Verhältnis 1 : AQ = AQ : AP zu bekommen, muß also AP gleich 2 · AR sein. Archytas fordert die Vorstellungskraft des Menschen enorm heraus, wenn man sich alle drei Bewegungen verknüpft anschaut.
Kommt der nächste Gauß aus Rußland oder China?
Einige werden jetzt einwenden, das gehe doch viel schneller, wenn man einfach den Taschenrechner nehme, dann habe ich die Lösung, und mehr will ich doch gar nicht.
Meinen Sie das tatsächlich? Die wirkliche Lösung muß ein anderes Denken im Kopf, eine neue Vorstellungskraft erzeugen. Sonst löst man das Problem nicht, sondern betrügt sich nur selber.
Muß man die Ähnlichkeit dieses Denkens mit der heutigen Lage der Wissenschaft extra hervorheben? Wir beten immer noch Hegel und Newton an; wir gelangen zum Mond – oder eben nicht mehr – nur mit wahnsinnig ausgetüftelten Näherungsmethoden, da das Newtonsche Gravitationsgesetz bei mehr als drei Körpern einfach nicht gilt. Wir bringen den Kindern die geisttötende Rechnerei der Algebra bei, ohne ihnen von der Geschichte dieser Rechenkunst zu erzählen und zu erklären, daß sie in Wirklichkeit eine Möglichkeit ist, die höhere Geometrie des Universums zu begreifen. Wer lernt heute schon diesen wunderschönen vierten Beweis des Fundamentalsatzes von Gauß? Oder seine Methode, mit der er den Asteroiden Ceres wiederentdeckte? Oder die Würfelverdoppelung des Archytas? Leibniz mit seiner hohen Vorstellung vom Menschen wird in keinem Lehrbuch erwähnt; Einstein ist zum „Schlagzeilenmacher“ degradiert. Wir sagen Ah! und Oh!, aber Einsteins Entdeckung der Gravitation als Geometrie, die auf der Geometrie von Riemann und Gauß aufbaut, wenden wir nicht an.
Doch es gibt Hoffnung! Wir Menschen haben eine Bestimmung, und die hat nichts mit dieser geistigen Bequemlichkeit, sondern mit Forschen, Nachdenken und Entdecken und neuen Ideen zu tun; wir sind in Wahrheit in der „wirklichen“ Welt zu Hause, wie es Gauß beschrieb:
„Es giebt in dieser Welt einen Genuß des Verstandes, der in der Wissenschaft sich befriedigt, und einen Genuß des Herzens, der hauptsächlich darin besteht, daß die Menschen einander die Mühsale, die Beschwerden des Lebens sich gegenseitig erleichtern. Ist das aber die Aufgabe des höchsten Wesens, auf gesonderten Kugeln Geschöpfe zu erschaffen und sie, um einen solchen Genuß zu bereiten, 80 oder 90 Jahre existiren zu lassen? – so wäre das ein erbärmlicher Plan. Ob die Seele 80 Jahre lebt oder 80 Millionen Jahre, wenn sie ein Mal untergehen soll, so ist dieser Zeitraum doch nur eine Galgenfrist.
Endlich würde es vorbei sein müssen. Man wird daher zu der Ansicht gedrängt, für die ohne eine strenge wissenschaftliche Begründung so vieles Andere spricht, daß neben dieser materiellen Welt noch eine zweite rein geistige Weltordnung existiert, mit eben so viel Mannigfaltigkeiten, als die in der wir leben – ihrer sollen wir theilhaftig werden.“
Mehr als die Hälfte der Menschheit, angefangen von den Chinesen und Russen, will einen Wirtschaftsaufbau, sie wollen wieder zum Mond und dann zum Mars, und studieren wieder die großen, denkfördernden Ideen eines Leibniz und Konfuzius. Sie lassen sich ihr Denken nicht kontrollieren und beten keine Götzen an. Gibt es vielleicht bald einen russischen oder chinesischen Gauß?
Fußnote(n)
- Vgl. http://www.spiegel.de/wissenschaft/mensch/numerator-raetseldes- moebiusbands-geloest-a-495189.html[↩]
- Briefwechsel mit Schumacher, 6, 107, abgedruckt in Daten aus dem Leben und Wirken von Carl Friedrich Gauß, zusammengestellt von Hans Salié in Leipzig.[↩]
- Gauß, Werke VIII, S. 221. [↩]
- Gauß, Werke VIII, S. 179.[↩]
- Siehe „Die vier Gauß’schen Beweise für die Zerlegung ganzer algebraischer Functionen in reele Factoren ersten oder zweiten Grades“, 1799–1849, hg. E. Netto, Verlag von Wilhelm Engelmann, Leipzig 1890.[↩]
- Gauß, Werke IV, S. 366[↩]
- Albert Einstein, Über die Spezielle und Allgemeine Relativitätstheorie (gemeinverständlich), F. Vieweg, Braunschweig 1920, S. 44[↩]
- C. F. Gauß, Die vier Gauß’schen Beweise a. a. O., S. 74.[↩]
