Zu Johannes Keplers 375. Todestag
Dieser Aufsatz ist Teil 65 der Serie „Riemann for Anti-Dummies“, auf englisch erschienen 2005.
„Gerade in so sorgenschwerer und bewegter Zeit wie der unsrigen, in welcher es schwer ist, Freude zu hegen an den Menschen und der Entwicklung der menschlichen Dinge, ist es besonders tröstlich, eines so großen, stillen Menschen wie Kepler zu gedenken. Er lebte in einer Zeit, in welcher das Verstehen einer allgemeinen Gesetzlichkeit des Natur-Ablaufes noch keineswegs gesichert war. Wie groß mußte sein Glaube an diese Gesetzlichkeit sein, daß er ihn mit der Kraft zu erfüllen vermochte, der der empirischen Erforschung der Planetenbewegung und der mathematischen Gesetzmäßigkeiten dieser Bewegung Jahrzehnte geduldiger schwerer Arbeit zu opfern, als ein Einsamer, von niemand Gestützter und wenig Verstandener! Wenn wir dies Andenken würdig ehren wollen, so müssen wir uns sein Problem und die Etappen von dessen Lösung möglichst deutlich vor Augen stellen.“
Dies waren die Worte, die Albert Einstein in der Frankfurter Allgemeinen Zeitung am 9. November 1930 zur Erinnerung an Keplers 300. Todestag schrieb. Heute, 75 Jahre später, klingen diese Worte immer noch wahr und sind ein geeigneter Ausgangspunkt, um das zu untersuchen, was damals wie heute unabdingbar ist: der Zusammenhang zwischen Erkenntnis und dem allgemeinen Lebensbedingungen der Menschheit.

Es ist ironischerweise lohnend, wenn man diesen Zusammenhang aus der Perspektive von Einsteins Sicht auf Kepler betrachtet. Einstein sah zwar die Bedeutung der Beziehung zwischen dem Zustand der Wissenschaft und dem Zustand der Gesellschaft, doch er verstand deren tieferen epistemologischen Implikationen nicht, wie Kepler es tat. Allerdings bestehen die Probleme, denen sich Einstein gegenüber sah, ungelöst bis heute weiter. Wenn man also Kepler aus der Sicht Einsteins und Einstein aus der Sicht Keplers sieht, läßt sich Keplers Herangehensweise an jene Probleme anwenden, die Einstein identifizierte.
Die Welt im November 1930 war tatsächlich eine „sorgenschwere und bewegte Zeit“, wie Einstein bemerkte. Eine globale Depression vertiefte sich, während die aus London agierenden internationalen synarchistischen Finanziers immer mehr ihre faschistische Kontrolle über die Regierungen von Europa und Japan festigten und den Plan verfolgten, gegen die Vereinigten Staaten loszuschlagen und ein globales neo-feudalistisches faschistisches Weltreich zu errichten. Wie Lyndon H. LaRouche bei vielen Gelegenheiten, u. a. in seinem Aufsatz „Globalisierung ist der Neue Imperialismus“, dargestellt hat, hatte diese Krise ihren Ursprung in der britisch-imperialen Reaktion auf die Niederlage der von ihr gesteuerten konföderierten Staaten Amerikas und die darauf folgende Verbreitung des Amerikanischen Systems nach Kontinentaleuropa und wesentliche Teile Asiens durch Abraham Lincolns Verbündete. Die britischen Imperialisten änderten lediglich ihre Strategie, um das Amerikanische System nicht primär mit militärischen Mitteln zu zerstören, sondern das kulturelle Umfeld zu unterwandern, auf dem die wissenschaftlichen Prinzipien dieses Systems basierte. Auf die gleiche Strategie hatte sich das antike Perser- und Babylonierreich verlegt, nachdem es ihnen im fünften vorchristlichen Jahrhundert mißlungen war, Athen und seine Verbündeten militärisch zu besiegen.
Diese Bemühungen hatten in Europa ihre größte Wirkung. In der Zeit nach der Amerikanischen Revolution organisierten die Briten in Frankreich den Jakobiner-Aufstand, ermöglichten Napoleons Diktatur und kontrollierten 1815 den Wiener Kongreß, von welchem sich eine Welle des Kulturpessimismus ausbreitete, der die europäischen Verbündeten Amerikas demoralisieren und den Optimismus zerstören sollte, der durch den Erfolg der Amerikanischen Sache entstanden war. Als dennoch in der zweiten Hälfte des 19. Jahrhunderts auf dem europäischen Kontinent Reformen im Geiste des Amerikanischen Systems in Angriff genommen wurden, intensivierte die Oligarchie den Kulturpessimismus weiter, wie er sich beispielsweise in der zunehmenden Verbreitung geisttötender Bewegungen wie des Existentialismus eines Friedrich Nietzsche und der Kultopern eines Richard Wagners ausdrückte.

In der Wissenschaft mündete der gleiche Kulturpessimismus in Angriffen auf die Leibniz-Tradition von Gauß, Dirichlet, Riemann und anderer. Beispiele hierfür waren die intellektuellen Betrügereien von Napoleons Lieblingsmathematiker Lagrange, die verbreitete Akzeptanz des britischen Empirismus von Maxwell, Lord Kelvin und anderen sowie die Wiedererstarkung des cartesischen Formalismus durch Cauchy. Zu Einsteins Zeit zeigte sich diese Degeneration in der Wissenschaft am deutlichsten in einer radikalen Irrationalität wie der „Kopenhagener Interpretation“ von Quanten-Phänomenen.
Einstein widersetzte sich zwar nachdrücklich dem Druck dieses radikalen Positivismus auf die Wissenschaft, doch er wurde schnell selbst zur politischen Zielscheibe des liberal-imperialen Flügels der Londoner Synarchisten. Man spielte auf seiner politischen Naivität und seinen kulturpessimistischen Neigungen, um einen politisch ahnungslosen Einstein manchmal mit Erfolg, manchmal ohne, für die eigenen Zwecke zu instrumentalisieren. Dadurch vergrößerte sich Einsteins Verwirrung über die Ursache der „bewegten Zeiten“, auf die er sich bezog, und tappte hinsichtlich ihrer Lösung im Dunkeln. Was er dennoch klar erkannte, war die parallele Degeneration der Gesellschaft und der Wissenschaft, von welcher er eine bessere, wenn auch unvollständige Vorstellung hatte.
Es überrascht nicht, daß Einstein in Kepler einen Geistesverwandten gefunden hat, dessen Verständnis für die Probleme von Wissenschaft und Gesellschaft viel tiefer als sein eigenes war. Zu Keplers Zeiten war die Irrationalität in der europäischen Gesellschaft ebenso verbreitet, obwohl Nikolaus von Kues und sein Umkreis nahezu zwei Jahrhunderte davor eine sehr viel höhere Ebene geistiger Gesundheit eingeleitet hatte. Damals hatten die Humanisten die Gelegenheit ergriffen, welche sich ihnen durch den Zusammenbruch der feudalistischen Bankhäuser Bardi und Peruzzi bot, um das sokratische Menschenbild als gesellschaftliches Prinzip durchzusetzen. Cusa betonte, genau wie Sokrates und Platon vor ihm, daß Erkenntnis eine charakteristische Eigenschaft des gesamten Universums ist, auch wenn sie allein der Mensch in selbstbewußter Form besitzt. Im Gegensatz zum aristotelischen Dogma, welches Europa seit dem Zusammenbruch der griechischen Gesellschaft in den Jahrhunderten nach dem Peloponnesischen Krieg beherrschte, verstand Cusa (wie Sokrates und Platon), daß das materielle Universum menschlichem Denken gegenüber nicht reaktionslos ist, sondern daß der Mensch mit seiner Fähigkeit, universelle physikalische Prinzipien zu entdecken, ein integraler Bestandteil der Selbstentwicklung des Universums als Ganzem ist.
Cusa ging noch weiter, indem er feststellte, daß die Organisation der menschlichen Angelegenheiten auf der Erkenntnis basieren müsse, welche Rolle der menschliche Geist in der materiellen Welt spiele. Seinen Kreisen gelang es, durch die Errungenschaften von Brunelleschi, Da Vinci, Pacioli in Kunst und Wissenschaft sowie durch die gesellschaftlichen Fortschritte, wie sie die Gründung der ersten Nationalstaaten durch Ludwig XI. in Frankreich und Heinrich VII. in England repräsentierten, in der Gesellschaft Fuß zu fassen.
Als Reaktion darauf versuchten die venezianischen Finanziers, die Erben des imperialen Rom, verzweifelt die feudale Kontrolle über Europa wieder zu gewinnen und das optimistische Menschenbild, das durch die Renaissance aufgekeimt war, zurückzudrängen. Angefangen mit der Spanischen Inquisition 1492 lösten Venedig und seine Verbündeten zahllose Religionskriege in Europa aus, was in der europäischen Kultur wieder ein fundamental irrationales Bild vom Menschen und dem Universum erzeugte. Gegen Ende von Keplers Leben kulminierte die Orgie der Verrücktheit in dem sogenannten Dreißigjährigen Krieg.
Aber Kepler verstand, daß die Verrücktheiten auf der Erde auch eine irrationale Sicht des Himmels bedingte. Die Astronomie zu seiner Zeit war schon längst von der ägyptisch-pythagoräischen Wissenschaft der „Sphärik“ abgekommen und auf die babylonisch-persische Sicht zurückgefallen, wonach der Mensch unfähig sei, etwas Wahres über die Natur der physischen Welt zu ent decken. Folglich müsse der Mensch alle irrationalen Dogmen akzeptieren, welche im Belieben der herrschenden Autoritäten lägen. Diese Sichtweise, welche die Wissenschaft zum reinen Sophismus reduzierte, diente dazu, dem Himmel eine Rechtfertigung für oligarchisch-imperiale Gesellschaftsformen unterzuschieben.
Unter Bezug auf Eratosthenes’ Beschreibung des Delischen Problems forderte Kepler, wie Platon vor ihm, seine Zeitgenossen auf zu erkennen, daß ihr falsches Bild von den Planetenbewegungen eine genauso falsche Sicht von ihnen selbst widerspiegelte. Wenn die Wissenschaftler und die Gesellschaft insgesamt die aristotelische Lehre akzeptierten, so sei dies die eigentliche Ursache des politischen und sozialen Zusammenbruches. Als überzeugter Anhänger Cusas betonte Kepler, daß sich die Grundprinzipien des Universums mit der Fähigkeit des menschlichen Geistes deckte, diese Prinzipien zu entdecken. Des weiteren ist die Existenz dieser Fähigkeit selbst ein Hinweis darauf, daß die Charakteristiken der menschlichen Kreativität auch Charakteristiken des Universums als Ganzem sind. Er schreibt dazu in seiner Dioptrice:
„Jeder, der sorgfältig darüber nachdenkt, wird zu dem Schluß gelangen (wenn er sich nicht nur auf den Glauben an die Heilige Schrift verlassen will), daß es einen Gott gibt, der alle Natur begründete, und daß er in deren Mechanik für die Menschen, die kommen würden, Sorge getragen hat. Denn dieses Welttheater ist so geordnet, daß darin geeignete Entwürfe existieren, durch die menschliche Geister, die gottähnlich sind, nicht nur eingeladen sind, die göttlichen Werke zu studieren, sondern auch bei deren tieferer Ergründung Beistand erhalten.“
Kepler verwarf den gemeinsamen Fehler von Ptolemäus, Kopernikus und Brahe, die sich treu an die Vorgabe des Aristoteles hielten, die Umlaufbahnen der Planeten müßten vollkommene Kreise sein. Statt dessen hielt sich Kepler an die Sicht des Nikolaus von Kues, wonach Veränderung eine für den Menschen und auch die physische Welt vorteilhafte Eigenschaft sei und deshalb die ungleichförmigen elliptischen Umlaufbahnen die Fähigkeit des Universums zur Selbstvervollkommnung besser ausdrückten als die mathematisch vollkommenen Kreise. Indem er anhand der Beobachtungsdaten zeigte, daß die Planetenbahnen tatsächlich ungleichförmig sind, und indem er die Gesetze fand, die diese Bewegung bestimmten, bewies Kepler nicht nur, daß das physikalische Universum auf Veränderung beruht, sondern daß der menschliche Geist auch in der Lage ist, diese zu erkennen.
Für Kepler existiert ein Planet als materielles Objekt nicht in einer rein materiellen Welt, und seine Umlaufbahn wird nicht rein von materiellen Prinzipien bestimmt. Vielmehr bezeichnet die historische und zukünftige Trajektorie des Planeten eine Bahn durch das Universum, in welchem die Prinzipien der Physik, des Lebens und der Erkenntnis allesamt überall und zu jeder Zeit wirksam sind. Die Prinzipien, die die Bewegung des Planeten bestimmen, führen demnach nicht nur den Planeten, sondern sie führen auch den menschlichen Geist zu ihrer Entdeckung. Wie Kepler betonte: der Geist ist ein Prinzip in der materiellen Welt.
Kepler brachte durch seine Erkenntnisse nicht nur die Astronomie weiter, sondern angesichts der vorherrschenden Irrationalität und Willkür in den wissenschaftlichen und gesellschaftlichen Angelegenheiten bekräftigte er ein optimistisches Konzept des Menschen und der Natur.
Zur Zeit Einsteins hatte die gleiche kulturelle Irrationalität wieder die Wissenschaft zu dominieren begonnen. Gegen Ende des 19. Jahrhunderts ließen immer mehr experimentelle Beobachtungen – wie der photoelektrische Effekt und Plancks Entdeckung der Quantisierung von Licht und Wärme – auf einen grundlegenden Unterschied in den physikalischen Eigenschaften beim Übergang vom makroskopischen zum mikroskopischen Bereich schließen. Diese Entdeckungen schlossen sich direkt an die früheren Arbeiten von Gauß, Fresnel, Riemann, Weber und anderen an, die in Erweiterung von Leibnizens Methode des Infinitesimalkalküls mikroskopische Prinzipien aus experimentell beobachteten makroskopischen Effekten entdeckt hatten. Riemann betonte deswegen in seiner Habilitationsschrift, daß es unwissenschaftlich sei, anzunehmen, man könne die Eigenschaften physikalischer Vorgänge im makroskopischen Bereich linear ins unendlich Kleine und unendlich Große erweitern. Statt dessen, betonte Riemann, müsse die Wissenschaft einen dynamischen Begriff der physischen Geometrie entwickeln, der das Potential nichtlinearer Veränderung zwischen diesen Bereichen widerspiegelt.
Riemann stellte fest:
„Auf der Genauigkeit, mit welcher wir die Erscheinungen ins Unendlichkleine verfolgen, beruht wesentlich die Erkenntnis ihres Causalzusammenhanges… In den Naturwissenschaften aber, wo die einfachen Grundbegriffe zu solchen Constructionen bis jetzt fehlen, verfolgt man, um den Causalzusammenhang zu erkennen, die Erscheinungen ins räumlich Kleine, so weit es das Mikroskop nur gestattet. Die Fragen über die Maßverhältnisse des Raumes im Unmeßbarkleinem gehören also nicht zu den müßigen.“
Im Gegenzug dazu versuchten die britischen Empiristen Kant und Euklid wiederzubeleben. Vor allem James Clerk Maxwell lehnte Riemanns Herangehensweise an die Physik ab und ließ einzig jene neoeuklidische Lehre gelten, die „jede Geometrie, die nicht die unsere ist“, ausschloß. Wenn man die Verhältnisse zwischen den beobachteten makroskopischen Wirkungen des Elektromagnetismus im Lichte der wachsenden Menge experimenteller Beweise für eine Änderung der physikalischen Eigenschaften im Mikroskopischen betrachtete, erwies sich Riemann daher als entscheidender Wegweiser, und Einstein erkannte das.
Unter Einsteins Zeitgenossen wurde es immer populärer, diese Phänomene mit Hilfe statistischer Methoden – ähnlich denen von Ptolemäus, Kopernikus und Brahe – zu „erklären“. Besonders haben sich hier Niels Bohr, sein Schützling Werner Heisenberg und Heisenbergs erster Lehrer, Max Born, hervorgetan.
Diese positivistische Sicht besagte, weil man keine mathematische Beschreibung dieser Phänomene außer der Statistik kannte, müsse das ganze Universum an sich zufällig sein. Mit anderen Worten, Bohr, Heisenberg, Born usw. behaupteten nicht bloß, daß sie die Prinzipien hinter diesen Erscheinungen nicht kannten, sondern daß es solche Prinzipien überhaupt nicht gab. Da keine Prinzipien existierten, könne man auch keine entdecken.
Born faßte seine Sicht dieses Streites in der Buchausgabe seines Briefwechsels mit Einstein so zusammen:
„Der hauptsächliche Grund für den Disput zwischen uns über die Gültigkeit statistischer Gesetze war folgender. Einstein war fest davon überzeugt, daß die Physik uns das Wissen der objektiv existierenden Welt liefern kann. Ich bin zusammen mit vielen anderen Physikern als Resultat der Erfahrungen im Bereich der atomaren Quantenphänomene nach und nach zu dem Standpunkt gelangt, daß dem nicht so ist. An jedem gegebenen Augenblick ist unser Wissen der objektiven Welt nur eine grobe Annährung, von der aus wir unbekannte (z. B. zukünftige) Zustände vorhersagen können, indem wir bestimmte Regeln wie die Wahrscheinlichkeitsgesetze der Quantenmechanik anwenden.“
Man kann nicht genug betonen, daß diese Sicht, die allgemein als die Kopenhagener Interpretation der Quantenphänomene bekannt ist, genau wie Ptolemäus‘ Astronomie keine Wissenschaft war. Es war ein sektenartiger Post-hoc-Glaube, welcher den vorherrschenden Existentialismus, der mit dem Vorstoß zu weltweiter faschistisch-oligarchischer Herrschaft verbunden war, zum Ausdruck brachte und schließlich auch dazu benutzt wurde, diesen zu rechtfertigen. In der Tradition des Babylonischen, Persischen und Römischen Reiches wollten die Londoner Imperialisten die erfolgreiche Verbreitung des kulturellen Optimismus, der mit dem amerikanischen Wirtschaftssystem einherging, aufhalten und zum Zeitalter der Zauberer und der Knechte zurückkehren.
Die axiomatischen Grundannahmen der Kopenhagener Schule sind inzwischen dermaßen fest in der öffentlichen Meinung verwurzelt, daß selbst Menschen, die von Physik überhaupt nichts verstehen, sie widerspruchslos hinnehmen. Ein Beispiel dafür ist die weitverbreitete Vorstellung, die Mandevillesche Lehre vom Freihandel sei einfach „die natürliche Ordnung der Dinge“.
Einstein, Planck und eine Handvoll anderer lehnten diesen radikalen Positivismus ab und verteidigten in den ersten Jahrzehnten des 20. Jahrhunderts hartnäckig das Kausalitätsprinzip in der Wissenschaft. Im September 1926 stellte Einstein gegenüber Born seine Sicht ganz deutlich dar:
„Die Quantenmechanik ist sehr achtung-gebietend. Aber eine innere Stimme sagt mir, daß das noch nicht der wahre Jakob ist. Die Theorie liefert viel, aber dem Geheimnis des Alten bringt sie uns kaum näher. Jedenfalls bin ich überzeugt, daß der nicht würfelt.“
Jahre später, im September 1944, faßte Einstein in einem Brief an Born seine Haltung, die er immer wieder zum Ausdruck gebracht hatte, so zusammen:
„In unserer wissenschaftlichen Erwartung haben wir uns zu Antipoden entwickelt. Du glaubst an den würfelnden Gott und ich an volle Gesetzlichkeit in einer Welt von etwas objectiv Seiendem, das ich auf wild spekulierendem Weg zu erhaschen suche. Ich glaube fest, aber ich hoffe, daß einer einen mehr realistischen Weg, bezw. eine mehr greifbare Unterlage finden wird, als es mir gegeben ist. Der große anfängliche Erfolg der Quantentheorie kann mich noch nicht zum Glauben an das fundamentale Würfelspiel bringen, wenn ich auch wohl weiß, daß die jüngeren Kollegen dies als Folge der Verkalkung auslegen. Einmal wird’s sich ja herausstellen, welche instinktive Haltung die richtige gewesen ist.“
Im September 1950, nachdem seine Verbindung mit Kurt Gödel sein historisches und epistemologisches Wissen erweitert hatte, schrieb Einstein an Born:
„Aus dem Schluß Deines Briefes sehe ich, daß auch Du die quantentheoretische Beschreibung als unvollständig auffaßt (Ensemble). Aber Du bist eben davon überzeugt, daß es für eine vollständige Beschreibung keine (vollständigen) Gesetze gibt, nach dem positivistischen Grundsatz esse est percipi. Nun, dies ist eine programmatische Einstellung, kein Wissen. Hier liegt die Haupt-Verschiedenheit unserer Einstellung. Einstweilen stehe ich allein mit meiner Meinung – wie Leibniz gegenüber dem absoluten Raum der Newtonschen Theorie. Nun hab ich Dir wieder etwas auf meinem alten Steckenpferd vorgeritten. Aber Du bist selber schuld, weil Du mich provoziert hast.“
Doch obwohl Einstein sich dem radikalen Positivismus der Kopenhagener Interpretation hartnäckig widersetzte und den Großteil seiner Bemühungen daransetzte, eine Vorstellung zu entwickeln, die diese ablösen sollte, scheiterte er – aus zwei verwandten Gründen. Erstens hatte er es, anders als Kepler und Leibniz, nicht geschafft, sich über den herrschenden Kulturpessimismus, der sich im Niedergang von Wissenschaft und Gesellschaft ausdrückte, ganz zu erheben, und zweitens erkannte er nicht, worauf sein Zeitgenosse Wernadskij hingewiesen hatte: daß die Fragen, die sich durch die Quantenphänomene in den Experimenten stellten, sich nicht im Bereich der Quantenphysik beantworten ließen. Indem er sich bei seiner Ablehnung der Kopenhagener Auslegung auf eine objektive Welt bezog, nahm Einstein stillschweigend den aristotelischen Sophismus hin, daß die Welt der Gedanken und die Welt der Physik zwei verschiedene Dinge seien. Tatsächlich lassen sich diese Fragen aber nur sinnvoll beantworten, wenn man erkennt – wie es Kepler tat –, daß die physikalischen Erscheinungen beobachtete Wirkungen in einem Universum sind, in dem Physik, Leben und Denken in einer, wie Riemann es nannte, vielfach verknüpften Mannigfaltigkeit ineinanderwirken.
Heute bietet nur die physikalische Wirtschaftswissenschaft, wie sie Lyndon LaRouche weiterentwickelt hat, eine angemessene Herangehensweise an diese Fragen. Dazu muß man verstehen, was Gauß und Riemann als hypergeometrischen Bereich beschrieben haben.
Das Universum von innen
Um ein erstes Verständnis davon zu gewinnen, wie diese hypergeometrische Vorstellung vom Universum entstand, können wir mit dem Problem beginnen, auf das Einstein sich in seiner Denkschrift für Kepler aus dem Jahr 1930 bezieht: die Bestimmung der Umlaufbahn der Erde um die Sonne. Dies war eine große Herausforderung, weil es bedeutete, die Erdbahn festzustellen, während man sich selbst auf der Erde befand, oder allgemeiner, die Bewegungen des Sonnensystems festzustellen, während man sich selbst im Sonnensystem bewegte.
Kepler wußte, daß jede wissenschaftliche Untersuchung bestimmter Fragen, wie z. B. eine Bestimmung der Marsumlaufbahn, tatsächlich nicht nur eine Untersuchung dieses Phänomens ist, sondern eine Untersuchung des ganzen Universums. Jeder Versuch, das Problem auf ein paar kleine Besonderheiten zu beschränken, wäre reine Spitzfindigkeit. Man kann dieses allgemeinere Problem so ausdrücken: Wie erkenne ich die ewige dynamische Natur des Universums aus der temporären Entfaltung dieser ewigen Dynamik heraus?
So schrieb Einstein 1930 in seinem FAZ-Artikel:
„Kopernikus hatte den besten Köpfen die Augen hierüber eröffnet, daß ein klares Begreifen der scheinbaren Bewegungen der Planeten am Himmel dadurch am besten zu gewinnen sei, daß man diese Bewegungen als Umlaufbewegungen der Planeten um die ruhend gedachte Sonne auffaßte. Wäre die Bewegung eines Planeten eine gleichmäßige Bewegung in einem Kreise um die Sonne als Mittelpunkt, so wäre es verhältnismäßig leicht gewesen, herauszufinden, wie diese Bewegungen von der Erde aus aussehen müssen. Da aber viel kompliziertere Erscheinungen vorlagen, so war die Aufgabe weit schwieriger. Es galt, jene Bewegungen zunächst einmal empirisch aus den Planetenbeobachtungen Tycho Brahes zu ermitteln. Dann erst konnte daran gedacht werden, die allgemeinen Gesetze zu finden, denen diese Bewegungen genügen. Um zu erfassen, wie schwierig schon die Aufgabe der Ermittlung der faktischen Umlauf-Bewegungen war, muß man sich folgendes klar machen: Man sieht nie, wo sich ein Planet zu einer bestimmten Zeit wirklich befindet, sondern nur in welcher Richtung er von der Erde aus jeweils gesehen wird, welch letztere aber selber eine Bewegung von unbekannter Art um die Sonne beschreibt. Die Schwierigkeiten scheinen alle so gut wie unüberwindlich. Kepler mußte einen Weg finden, um in dieses Chaos Ordnung zu bringen. Zunächst erkannte er, daß zuerst versucht werden mußte, die Bewegung der Erde selbst zu ermitteln.“
Wie Einstein anmerkt, läßt sich die Bewegung der Planeten im Sonnensystem nicht unmittelbar beobachten. Beobachten kann man nur die relativen Positionen von Sonne, Planeten und Fixsternen, wie man sie von der Erde aus sieht. Die beobachteten Veränderungen der relativen Positionen gehen auf eine Kombination von Bewegungen zurück. Um also z. B. die Bewegung des Mars zu bestimmen, wie Kepler es sich vorgenommen hatte, mußte man erst entwirren, welche der beobachteten Veränderungen der Positionen von Mars, Erde, Sonne und Fixsternen jeweils auf deren eigene Bewegung zurückgingen.
Ptolemäus, Kopernikus und Brahe hatten unterschiedliche mathematische Mittel zur Entwirrung dieser Bewegungen gefunden. Die Schwierigkeit für Kepler lag darin, daß keine dieser Lösungen stimmte, ja nicht einmal diesen Anspruch erhob. Kepler versuchte im Sinne Cusas, die beobachteten Bewegungen als Funktion der wahren Ursachen zu verstehen.
Aber er konnte diese Ursachen nicht direkt beobachten; er mußte also die Begrenzungen der Sinneswahrnehmung überschreiten und sich die beobachteten Bewegungen von einem Standpunkt aus vorstellen, der nur durch Vernunft erreichbar war.
Doch bevor er die wahren Ursachen herausfinden konnte, mußte Kepler die Beobachtungen der Bewegungen kennen, wozu er ebenfalls die Grenzen der Sinneswahrnehmung überschreiten mußte. Im Falle des Mars mußte er zuerst das Verhältnis des Mars zur Erde und zur Sonne herausfinden. Dazu mußte er die Bewegung der Erde kennen, die er nicht selbst beobachten konnte. Folglich mußte er sich vorstellen, wie die Erdbewegung aussähe, wenn er sich auf dem Mars befände, dessen Bewegung er auch nicht kannte!
Kepler hat seine Herangehensweise in der Neuen Astronomie im einzelnen dargelegt, aber im Großen und Ganzen ging er so vor: Von der Erde aus kann man die scheinbare Bewegung der Sonne durch den Tierkreis im Laufe eines Jahres beobachten. Kepler ging davon aus, daß diese scheinbare Bewegung der Sonne ein Ausdruck der tatsächlichen Bewegung der Erde sei. Daß diese Bewegung zyklisch war, ließ eindeutig darauf schließen, daß die Erdbewegung eine in sich geschlossene Bahn darstellte. So konnte er sich vorstellen, wie ein Beobachter auf der Sonne die Erde sähe.
Die Erde vom Mars aus zu betrachten, war schwieriger, weil sich der Mars anders als die Sonne auch selbst bewegte. Zur Lösung dieses Problems begann Kepler mit der Bestimmung der Position von Mars und
Sonne im Tierkreis in dem besonderen Augenblick, wenn Sonne, Erde und Mars in einer geraden Linie zueinander stehen (Abbildung 1).
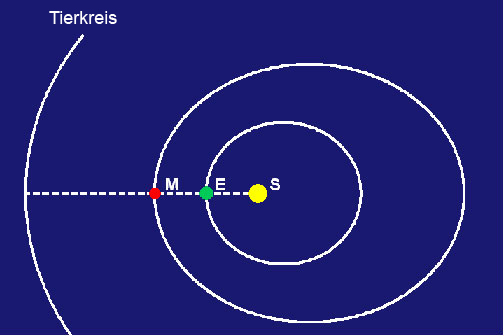
Man nennt diese Konstellation Opposition; es gab sie zuletzt am 7. November 2005. Zu diesem Zeitpunkt wird ein Beobachter auf der Erde den Mars an einer bestimmten Stelle im Tierkreis sehen, und ein Beobachter auf dem Mars sähe Erde und Sonne an einer Stelle im Tierkreis direkt gegenüber der Position des Mars.
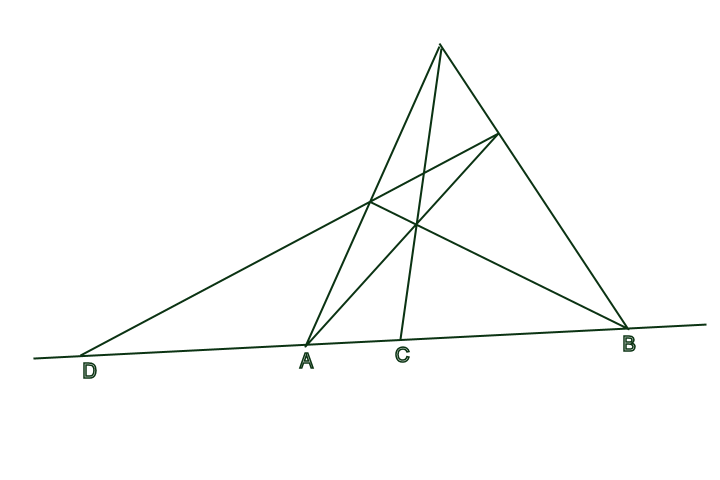
An einem bestimmten Punkt nach dieser Beobachtung (frühere Beobachtungen hatten ergeben, daß dieser Zeitraum 687 Erdentage betrug) wird der Mars an die Stelle in seiner Bahn zurückkehren, an der er war, als er Erde und Sonne gegenüberstand. Aber dann wird sich die Erde an einer anderen Stelle ihrer Bahn befinden, und deshalb wird man den Mars an einer anderen Stelle im Tierkreis sehen (Abbildung 2).
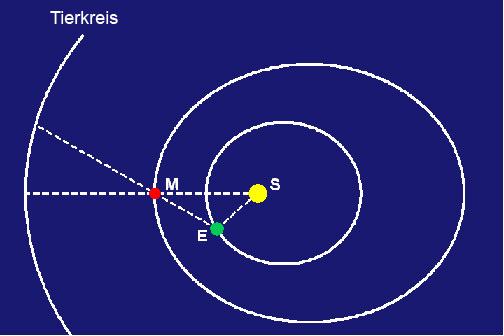
Ein Beobachter auf dem Mars sähe allerdings jetzt die Sonne an derselben Stelle im Tierkreis, an der sie 687 Erdtage vorher gewesen war. Doch er sähe eine Veränderung der Position der Erde im Tierkreis über diesen Zeitraum. Diese Beobachtungen bilden ein Dreieck zwischen Erde, Sonne und Mars mit der geraden Linie zwischen den drei Objekten bei der ersten Opposition als Grundlinie und den Sichtlinien Erde-Mars und Erde-Sonne an dieser neuen Position der Erde als Seitenlinien. Indem er die Beobachtungen aus diesen drei Blickpunkten miteinander verglich, konnte Kepler die Winkel dieses Dreiecks bestimmen. Und indem er diese Berechnung anhand der ausführlichen zwanzigjährigen Aufzeichnungen von Tycho Brahes Beobachtungen ständig wiederholte, konnte Kepler die Umlaufbahn der Erde genau bestimmen (Abbildung 3).
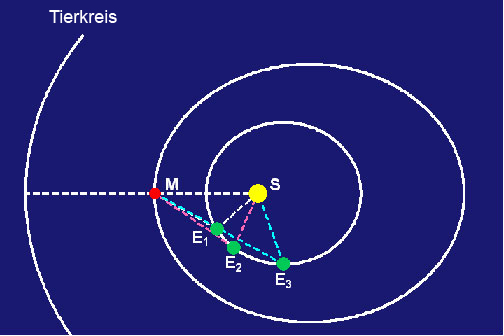
Nachdem er auf diese Weise die Erdbahn bestimmt hatte, wandte Kepler sich der Bestimmung der Marsbahn zu. Wir verweisen den Leser auf die ausführliche Darlegung dieser Entdeckung in Keplers Neuer Astronomie, aber ein Punkt ist für das folgende zu betonen.
Nachdem Kepler die Größe der Erdbahn und ihre exzentrische Position im Verhältnis zur Sonne bestimmt hatte, stellte er fest, daß die Bahn des Mars ebenfalls exzentrisch zur Sonne verlief. Er war zuerst davon ausgegangen, daß die Umlaufbahnen von Mars und Erde kreisförmig seien. Für die Erde war das annähernd richtig, weil die Exzentrizität der Erde ziemlich klein ist. Aber bei Mars wich die Exzentrizität beträchtlich von der reinen Kreisform ab. Kepler entdeckte dies, als er die beobachteten Positionen des Mars mit den geometrischen Eigenschaften eines Kreises verglich – daß nämlich drei eindeutige Positionen ausreichen, um einen Kreis genau zu bestimmen. Unter dieser Annahme müßten drei beliebige Positionen des Mars auf demselben Kreis liegen. Aber nachdem er 79 Kombinationen von je drei Positionen überprüft und dabei festgestellt hatte, daß alle 79 auf jeweils verschiedenen Kreisen lagen, wurde Kepler klar, daß er es nicht mit einer kreisförmigen Umlaufbahn zu tun hatte, und unter viel Mühe und Arbeit bewies er, daß diese Bahn eine Ellipse war, in deren einem Brennpunkt die Sonne lag.
Die Schatten entwirren
Wie schon gesagt, versuchte Kepler bei der Arbeit an der Bestimmung der Marsbahn das Wesen des ganzen Universums zu bestimmen – des Universums, welches das Sonnensystem hervorgebracht hatte, mitsamt einer Erde, die im Laufe der Zeit vom Leben beherrscht und von denkenden Menschen bewohnt wurde, die ihre Gesetze erforschten.
Kepler wurde klar, daß er, um diese zugrundeliegenden Prinzipien astronomisch zu erforschen, auch diesen Vorgang selbst, wie er das tat, erforschen mußte. So wie er die Bewegungen im Sonnensystem aus dem Innern des Sonnensystems heraus feststellen mußte, um die Natur des Universums kennenzulernen, mußte er eine selbstbewußte Vorstellung der Rolle seines eigenes Geistes bei der Entwicklung dieses Universums entwickeln. Er mußte mehreres gleichzeitig untersuchen: die Verbindung zwischen den physikalischen Teilen des Universums, deren Wechselwirkung mit seinen Sinnen, die Wechselwirkung dieser Sinne mit seinem Geist und die Wechselwirkung seines Geistes mit dem ganzen Universum.
Er erkannte: Da alle astronomischen Beobachtungen aus der Wechselwirkung zwischen Licht und menschlichem Auge folgten, würde ihm das Wissen der Gesetze von Licht und Sehen eine Verbindung zwischen dem kognitiven und dem physikalischen Bereich liefern. So schrieb er in der Einleitung seiner Optik:
„Was Wunder dann, wenn dieses Prinzip aller Zierde der Welt, welches der göttliche Moses unmittelbar am ersten Tag in die kaum geschaffene Materie einführte, eine Art Werkzeug des Schöpfers, allem Form und Wachstum zu geben. wenn dieses Prinzip, sage ich, das Herausragendste in der ganzen Körperwelt, die Grundsubstanz alles Belebten und die Kette zwischen der Körper- und Geisterwelt, in dieselben Gesetze übergegangen ist, nach denen die Welt eingerichtet werden sollte.“
In der Optik erläutert Kepler, wie diese Übereinstimmung zwischen den Gesetzen der Physik und der Erkenntnis sich im Ausdruck der elliptischen Planetenbahnen und den Eigenschaften von Licht und Sehvermögen als Sonderfällen einer einheitlichen Vorstellung einer Kegelfunktion widerspiegelt.
Es ist an dieser Stelle wichtig, eine weitverbreitete Legende, die an praktisch allen mathematischen Fachbereichen von höheren Schulen und Universitäten ständig wiederholt wird, als falsch zu entlarven. Die heutigen Mathematiker behaupten, die Griechen hätten die Kegelschnitte nur aus rein mathematischem Interesse untersucht, ohne jede Rücksicht auf ihre Bedeutung für die reale Welt. Als Kepler herausfand, daß die Planetenumlaufbahnen elliptisch sind, sei das deswegen eine große Überraschung gewesen, im Sinne der bloß mathematischen Erwägungen der Griechen rein zufällig.
Das ist völlig falsch. Die griechischen Untersuchungen der Kegelschnitte entstanden aus den Forschungen der Pythagoräer zur Verdoppelung des Würfels. Wie Platon im Timaios erklärt, erforschte man damit gleichzeitig die Eigenschaften des physikalischen Universums, die Art und Weise, wie sich diese Eigenschaften im menschlichen Geist widerspiegeln, und die Wechselwirkungen zwischen dem menschlichen Geist und dem Universum als ganzem. Insofern war Keplers Entdeckung, daß die Planetenbahnen eine andere Form derselben Kegelfunktion ausdrückten, nicht nur kein Zufall, sie war auch keine Überraschung – höchstens für die Mathematiker von heute.
Darüber hinaus wußte Kepler, als er die Kegelschnitte in Hinsicht auf die Planeten entdeckte, daß dies universelle Bedeutung hatte; wie Archytas’ Konstruktion der Verdoppelung des Würfels durch Torus, Zylinder und Kegel zeigte, ist die typische Wirkung im physikalischen Universum nicht einfach nur kugelförmig, sondern von einer höheren Art, welche Gauß und Riemann später hypergeometrisch nennen sollten.
Diese höhere Hypergeometrie taucht auf, wenn man die allgemeine Form einer einfachen Kegelfunktion untersucht, deren physikalische Manifestationen die elliptischen Umlaufbahnen und die Verdoppelung des Würfels sind. In seiner Optik erforschte Kepler diese Kegelfunktion aus dem Blickwinkel von Licht und Sehen.
Aus der einen Perspektive erzeugt man die Kegelschnitte durch die Bewegung einer Fläche, die einen Kegel schneidet (Abbildung 4).
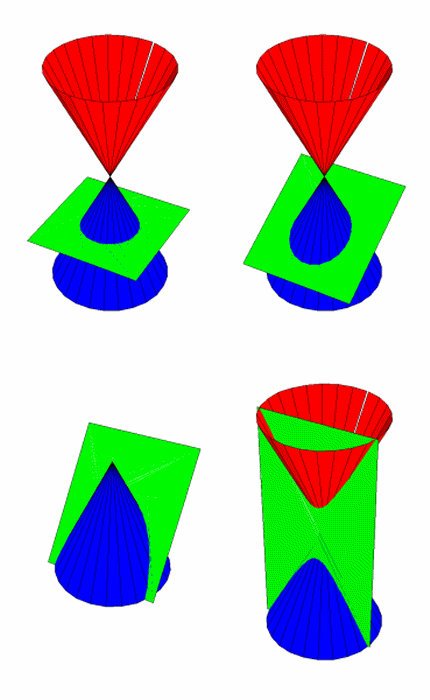
Betrachtet man aber die Projektion auf eine Fläche, so taucht beim Übergang vom Bereich der elliptischen Wirkung zu dem der hyperbolischen eine Diskontinuität auf (Abbildung 5).

Wie Kepler schreibt:
„Analog statt geometrisch gesprochen, gibt es unter diesen Linien aufgrund ihrer Eigenschaften die folgende Ordnung: Es verläuft von der Geraden über eine Unendlichkeit von Hyperbeln zur Parabel und von dort über eine Unendlichkeit von Ellipsen zum Kreis. Denn die stumpfwinkligste aller Hyperbeln ist eine Gerade, die spitzwinkligste eine Parabel. Ähnlich ist die spitzeste aller Ellipsen eine Parabel; die stumpfeste ein Kreis. So hat die Parabel auf der einen Seite zwei Dinge, die von ihrem Wesen her unendlich sind: die Hyperbel und die Gerade, und auf der anderen Seite zwei Dinge, die endlich sind und zu sich selbst zurückkehren: die Ellipse und den Kreis. Sie selbst hält sich mit einem mittleren Wesen in der Mitte. Denn sie ist auch unendlich, nimmt aber andererseits eine Begrenzung an, denn je ausgedehnter sie ist, desto mehr wird sie sich selbst parallel und streckt ihre Arme (sozusagen) nicht wie eine Hyperbel aus, sondern zieht sich von der Umarmung des Unendlichen zurück und sucht immer weniger, obwohl sie immer mehr einschließt. Bei der Hyperbel ist es so, daß sie umso mehr sucht, je mehr sie wirklich in den Armen einschließt. Deshalb sind die entgegengesetzten Grenzen der Kreis und die Gerade: ersterer ist reine Gekrümmtheit, letztere ist reine Geradheit. Hyperbel, Parabel und Ellipse stehen dazwischen und haben Anteil am Geraden und am Gekrümmten, die Parabel gleichmäßig, die Hyperbel mehr vom Geraden und die Ellipse mehr vom Gekrümmten.“
Kepler zeigte weiter, daß die epistemologische Bedeutung der elliptischen Natur der Planetenbahnen sich nicht nur im Verhältnis zu Licht und Sehen ausdrückt. Insbesondere in seiner Weltharmonik legte er dar, wie die Verhältnisse der bestimmenden minimalen und maximalen Geschwindigkeit entlang der elliptischen Bahnen mit den Verhältnissen in der wohltemperierten Polyphonie, die Johann Sebastian Bach später in seinen Kompositionen entfalten sollte, übereinstimmen. Auch hier tauchte eine Diskontinuität auf, die physikalische Bedeutung hatte – nämlich die Existenz der lydischen Intervalle zwischen den Bahnen von Mars und Jupiter und dem Asteroidengürtel, der damals noch gar nicht entdeckt war! Diese physikalische Diskontinuität als Punkt der Veränderung (eine Art Registerwechsel) spiegelt sich auch darin wider, daß die Planeten auf verschiedenen Seiten dieser Diskontinuität physikalisch unterschiedlich beschaffen sind. Diese harmonische Beziehung und die damit einhergehende Diskontinuität stammen im Kern noch von der harmonisch organisierten Plasmascheibe her, aus der sich das Sonnensystem entwickelt hat.
Die spätere Entdeckung der hyperbolischen Bahnen von Kometen sowie Gauß’ Bestimmung der Bahn des Asteroiden Ceres zeigten, daß Kepler mit seiner Auffassung, die elliptischen Umlaufbahnen seien ein Sonderfall einer allgemeineren Kegelfunktion, recht hatte. Dieses verallgemeinerte Verständnis von Keplers Astronomie hat Gauß in seiner Theorie der Bewegung der Himmelskörper, welche in Kegelschnitten die Sonne umlaufen, zusammengefaßt.
Gauß und sein Schüler Riemann gingen noch weiter und legten dar, daß Keplers allgemeine Kegelfunktion selbst ein Sonderfall einer allgemeineren, hypergeometrischen oder hyperkonischen Funktion war. Diese hypergeometrischen Funktionen drückten nicht die Eigenschaften des Sonnensystems an sich aus, sondern die Eigenschaften des Universums, die diese Eigenschaften des Sonnensystems erst hervorgebracht hatten.
Das nicht-unendliche Universum
Indem er die Kegelfunktionen als einheitliche Konzeption der physikalischen, biologischen und kognitiven Bereiche der Astronomie ansah, führte Kepler den von Cusa begonnenen Prozeß, die Wissenschaft auf die höhere Ebene der vor-euklidischen Griechen zurückzuführen, fort und bereitete den Weg für die späteren Erkenntnisse von Kästner, Gauß und Riemann. Das bedeutete, die Wissenschaft von den verderblichen Auswirkungen einer Kettung an die euklidische Geometrie zu befreien.
Ein einscheidender Ansatzpunkt für Cusa und Kepler war, den falschen und willkürlichen aristotelischen Begriff des mathematischen Unendlichen, wie er in Euklids Elementen überdauert hat, zu zerstören. Wenn der Raum, wie Euklid behauptete, unendlich in drei geradlinige Richtungen ausgedehnt wäre, dann wäre nur einheitliche kreisförmige oder geradlinige Bewegung möglich. In einem solchen Fantasiekonstrukt könnten die experimentell festgestellten ungleichförmigen elliptischen Planetenbahnen nur als eine willkürliche Abweichung in einer Welt vorkommen, in der keine Veränderung denkbar wäre.
Wie Abraham Kästner später feststellte, steht und fällt die formale Gültigkeit der euklidischen Geometrie mit dem Parallelenpostulat. Euklid war sich dieser Schwäche offenbar sehr bewußt und erwähnte daher in seiner Definition das Unendliche nicht direkt. Auch in den Beweisen der späteren Postulate benutzte er das Parallelenpostulat nur sehr sparsam. Nichtsdestotrotz, wie Gauß und Kästner betonten, gibt es ohne das Parallelenpostulat keine ähnlichen Dreiecke, und ohne ähnliche Dreiecke bricht das gesamte Gebäude der euklidischen Geometrie in sich zusammen. Gauß ging noch weiter als Kästner, indem er betonte, daß das Parallelenpostulat nur unter der Annahme wahr sein könne, daß die Krümmung des physischen Raumes null wäre – eine Tatsache, welche nur durch physische Messung, nicht durch den mathematischen Formalismus der euklidischen Geometrie bestimmt werden könnte.
Subjektiv gesehen erfordert der Glaube an eine der euklidischen Geometrie entsprechende physische Realität, Kants Axiom zu akzeptieren, wonach der menschliche Geist praktisch festverdrahtet sein muß, um sich das Universum nach euklidischen Maßstäben vorstellen zu können. Doch wie Archytas bereits in der Antike zeigte, ist die Verdopplung des „euklidischen“ Würfels von höheren Kegelfunktionen abhängig, was Kants Ehrerbietung für die euklidische Geometrie widerlegt. Keplers projektive Konstruktion der Kegelschnitte ist eine weitere Demonstration, daß solch eine Kantsche Sicht völlig illusorisch ist.
In Keplers Konstruktion taucht das Unendliche nicht als eine unerreichbare, unbestimmte Größe auf, sondern als Umschlagspunkt – als Übergang zwischen dem elliptischen und dem hyperbolischen Wirkungsbereich, verbunden durch eine einzige Kegelfunktion. Von Keplers Standpunkt aus liegt das Unendliche demnach in der Mitte und nicht am Ende einer nicht-unendlichen selbstbegrenzten Mannigfaltigkeit.
Die experimentellen und epistemologischen Argumente für ein solches nicht-unendliches Universum hatte Platon bereits in seinem Timaios dargestellt. Cusa und Kepler griffen diese Überlegungen wieder auf und führten sie weiter. In seinem Werk Über die belehrte Unwissenheit betont Nikolaus von Kues, daß das scheinbar Unendliche in der „entfalteten“ Form eines selbstbegrenzten, „eingefalteten“ Universums in Erscheinung tritt. In der entfalteten Form scheinen Gegensätze wie Maximum und Minimum unterschiedlich zu sein, aber in der eingefalteten Form stimmen solche Gegensätze überein. Im Jahre 1610 entwickelte Kepler ein physikalisches Argument für Cusas Vorstellung der Selbstbegrenztheit: Wenn das Universum unendlich wäre, wäre der Nachthimmel nicht dunkel, sondern vom Licht unendlich vieler Sterne erleuchtet. Die Darstellung dieses Paradoxes wird heute Wilhelm Olbers, dem engen Freund von Gauß, zugeschrieben, der es fast zweihundert Jahre nach Kepler in seiner Argumentation gegen Kant wieder aufgriff.
In seiner Habilitationsschrift äußerte sich auch Riemann über ein nicht-unendliches Universum:
„Bei der Ausdehnung der Raumkonstructionen in’s Unmeßbargroße ist Unbegrenztheit und Unendlichkeit zu scheiden; jene gehört zu den Ausdehnungsverhältnissen, diese zu den Maßverhältnissen. Daß der Raum eine unbegrenzte dreifach ausgedehnte Mannigfaltigkeit sei, ist eine Voraussetzung, welche bei jeder Auffassung der Außenwelt angewandt wird, nach welcher in jedem Augenblicke das Gebiet der wirklichen Wahrnehmung ergänzt und die möglichen Orte eines gesuchten Gegenstandes construirt werden und welche sich bei diesen Anwendungen fortwährend bestätigt. Die Unbegrenztheit des Raumes besitzt daher eine größere empirische Gewißheit, als irgend eine äußere Erfahrung. Hieraus folgt aber die Unendlichkeit keineswegs; vielmehr würde der Raum, wenn man Unabhängigkeit der Körper vom Ort voraussetzt, ihm also ein constantes Krümmungsmaß zuschreibt, nothwendig endlich sein, so bald dieses Krümmungsmaß einen noch so kleinen positiven Werth hätte.“
Wie Cusa hervorhob, entspricht diese antieuklidische Vorstellung eines selbst-begrenzten Universums sowohl der Natur der physischen Welt als auch der des Menschen. Wie die physische Welt ist das Leben des Menschen endlich, aber unbegrenzt. Es beginnt mit der Geburt und endet mit dem Tod. Vom Standpunkt der Sterblichkeit erscheint die Welt vor der Geburt und nach dem Tod unendlich weit entfernt. Aber durch die Übermittlung schöpferischer Entdeckungen durch die Kultur beeinflußt der Mensch in seinem endlichen Leben alles, was ihm vorherging und was ihm folgt, und wird davon beeinflußt. Die scheinbar unendlichen Bereiche, jenseits der zeitlichen Grenzen, liegen nicht außerhalb des sterblichen Lebens, sondern in seinem Mittelpunkt.
Das heißt, wenn man an die euklidische Geometrie glaubt, verneint man die Unsterblichkeit der menschlichen Seele.
Cusas und Keplers Ungültigkeitserklärung der euklidischen Geometrie bereitete den Weg für die Entwicklung eines neuen, physikalisch begründeten Konzeptes einer nicht-unendlichen Geometrie. Die ersten Schritte in diese Richtung unternahm Girard Desargues (1591–1661), der die euklidische Geometrie zugunsten von Keplers projektiven Beziehungen verwarf und so das aristotelische Konzept des Unendlichen vollständig aus der Wissenschaft verbannte.
Zur Verdeutlichung von Desargues’ Methode kann man ein einfaches Experiment durchführen. Man zeichne ein großes Rechteck an eine Tafel. Die gegenüberliegenden Seiten scheinen nach den Vorgaben der euklidischen Geometrie parallel zu sein und schneiden sich also nie, selbst wenn man sie unendlich verlängert. Jetzt nehme man eine durchsichtige Kunststoffscheibe und halte sie in einem Winkel an die Tafel. Mit einem geschlossenen Auge übertrage man die Umrisse des Rechtecks auf die Scheibe. Dadurch entsteht eine konische Projektion der Tafel auf die Ebene der Kunststoffscheibe mit dem Auge als Kegelspitze. Unter dieser Projektion schneiden sich auf der Scheibe die gegenüberliegenden Seiten des Rechtecks, welche auf der Tafel parallel zu sein scheinen. So wird mit einer einfachen Wendung des Kopfes das Unendliche ins Endliche gebracht!
Auf diese Weise begann Desargues Keplers Fortführung der Cusanischen Idee eines nicht-unendlichen Universums allgemeiner zu fassen, woraus viele wichtige Entdeckungen entstanden, die für die spätere Entwicklung der Wissenschaft entscheidend waren. Eine davon ist für unsere Argumentation hier von besonderer Bedeutung.
Desargues zeigte, daß, obwohl sich bei der Projektion Längen, Längenverhältnisse und Winkel im allgemeinen ändern, ein Merkmal unverändert bleibt. Dieses Merkmal ist das Verhältnis zweier Verhältnisse, die zwischen vier beliebigen Punkten gebildet werden – später auch Kreuzverhältnis genannt (Abbildung 6).
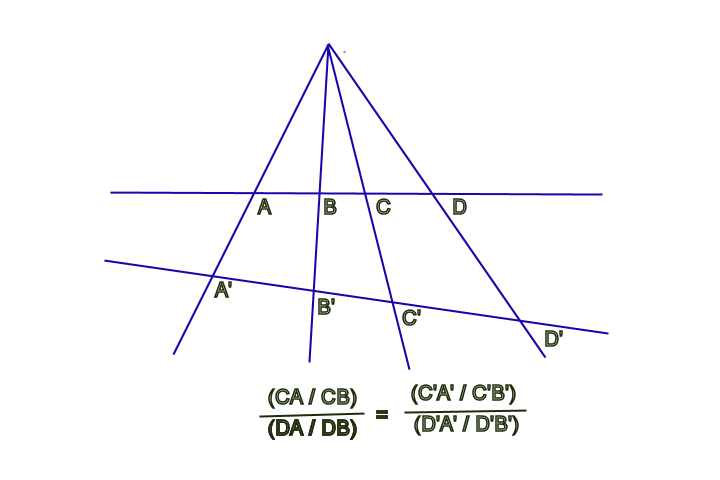
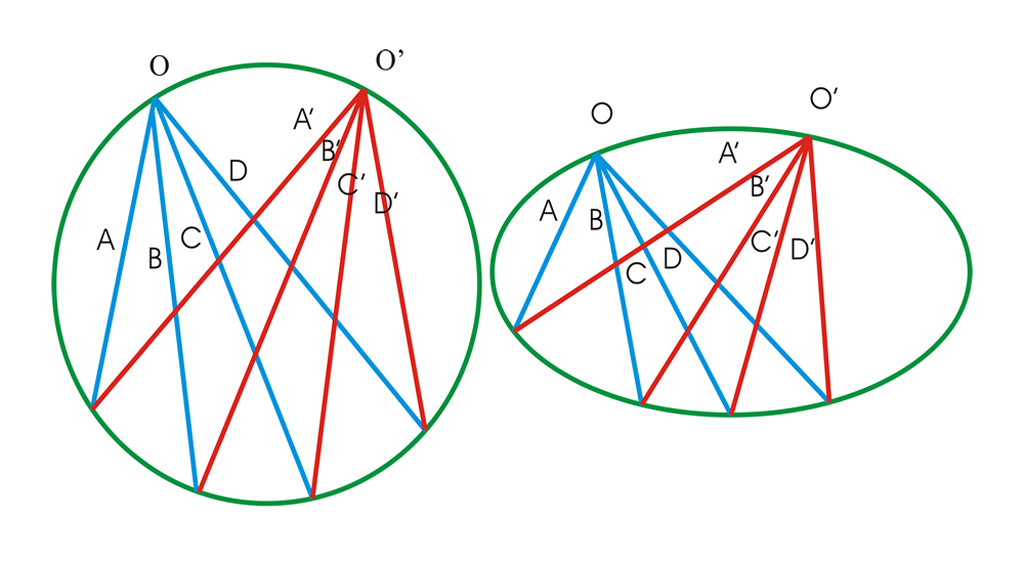
Da die Kegelschnitte in einem projektiven Verhältnis zueinander stehen, ist die Invarianz des Kreuzverhältnisses ein Kennzeichen der Kegelfunktion (Abbildung 7).
Eine weitere Illustration des gleichen Prinzips läßt sich einer anderen Entdeckung von Desargues entnehmen – dem vollständigen Viereck. Desargues bewies, daß die Schnittpunkte der verlängerten Seiten und Diagonalen eines beliebigen Vierecks eine projektive Konfiguration bilden, in der die Kreuzverhältnisse erhalten bleiben (Abbildung 8).
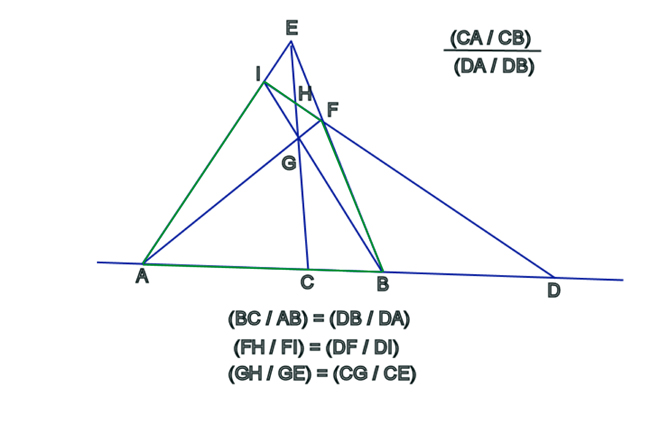
Diese Art Kreuzverhältnis ist ein Sonderfall, den man harmonisch nennt, da C die Strecke AB im selben Verhältnis teilt wie B die Strecke AD. Betrachtet man sich das vollständige Viereck nun dynamisch und stellt sich in der Tradition Keplers vor, daß der Punkt D sich in Richtung des Unendlichen zu einer Seite hin bewegt, dann müssen sich die Punkte A, B und C ebenfalls bewegen, um das harmonische Verhältnis zwischen allen vier Punkten zu erhalten. Diese Bewegung verändert auch die Winkel des Vierecks.
Wenn die Seiten des Vierecks parallel werden, erreicht Punkt D das Unendliche, oder umgekehrt, wenn D das Unendliche erreicht, werden die Seiten des Vierecks parallel. An diesem Punkt ist das harmonische Kreuzverhältnis mit den Punkten A, B und C immer noch erhalten (Abbildung 9).
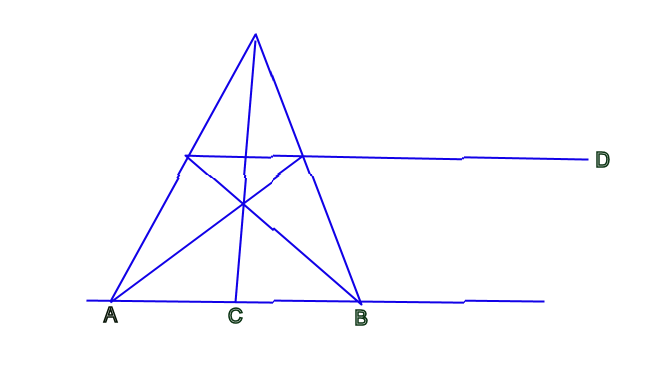
Neigt man nun die Seiten des Vierecks ein wenig mehr, erscheint Punkt D aus dem Unendlichen auf der anderen Seite von Punkt A wieder, während die harmonischen Verhältnisse der Punkte A, B und C weiter erhalten bleiben (Abbildung 10).
Vom Standpunkt der euklidischen Geometrie scheint die harmonische Charakteristik des vollständigen Vierecks mystisch, weil in der euklidischen Geometrie das Unendliche keinen Effekt auf das Endliche haben kann. Aber wie Desargues’ Konstruktion zeigt, ist das „Unendliche“ im vollständigen Viereck, wie in Keplers projektiven Kegelschnitten, nur ein Umschlagspunkt, der – wie jeder „endliche“ Punkt auch – ein harmonisches Verhältnis zu den endlichen Teilen behält.
Derlei Paradoxe offenbaren das Dilemma der euklidischen Sophisten: entweder man behält die euklidische Geometrie bei und behauptet einfach, daß die harmonischen Eigenschaften des vollständigen Vierecks magisch sind, oder man erkennt, wie Kepler es tat, daß die physikalischen Prinzipien nach den experimentellen Beobachtungen derartige harmonische Verhältnisse ausdrücken, und gibt damit zu, daß die euklidische Geometrie Betrug ist.
Das vollständige Viereck ist eigentlich ein frühes Beispiel für das, was Riemann später das „Dirichlet-Prinzip“ nannte. Zwischen den Positionen der Punkte A, B, C und D und den Winkeln und Längen der Seiten und Diagonalen des Vierecks gibt es eine einfach zusammenhängende Beziehung, welche eine Wirkung des harmonischen Prinzips ist, das sich in der Invarianz des Kreuzverhältnisses widerspiegelt. Dieses harmonische Prinzip ist das Primäre, und die Positionen der sichtbaren Objekte sind Funktionen dieses harmonischen Prinzips.
Die harmonische Beziehung bleibt auch dann bestehen, wenn ein Punkt scheinbar unendlich weit entfernt ist, denn der Punkt im Unendlichen liegt nicht außerhalb, sondern innerhalb des Prozesses. Was unendlich zu sein scheint, ist lediglich ein Umschlagspunkt innerhalb einer ansonsten nicht-unendlichen selbstbegrenzten Mannigfaltigkeit.
Das vollständige Viereck und Keplers Kegelschnitte können in einem euklidischen unendlich ausgedehnten Raum nicht bestehen; sie gibt es nur in einer Cusanisch-Keplerischen nicht-unendlichen Mannigfaltigkeit. In einer solchen Mannigfaltigkeit ist Veränderung eine wesentliche Eigenschaft, und was als mathematisch unendlich erscheint, wird als Ausdruck dieser Veränderung aufgefaßt.
Der Weg zum Hyperkonischen
Im Anschluß an Desargues wurden Keplers Kegelfunktionen durch Blaise Pascal und Leibniz weiter ausgearbeitet. In seiner Entwicklung des Infinitesimalkalküls zeigte Leibniz, daß Kegelfunktionen drei verschiedene, aber verwandte Formen haben: exponentiell, kreisförmig und hyperbolisch. In Zusammenarbeit mit Bernoulli zeigte Leibniz, daß die Kettenlinie ein physischer Ausdruck der drei Formen von Kegelfunktionen ist. Damit war einmal mehr belegt, daß sich die physischen Eigenschaften des Universums mit dem Cusanisch- Keplerischen Konzept einer nicht-unendlichen selbstbegrenzten Mannigfaltigkeit decken. Doch bereits in Keplers Astronomie selbst war der experimentelle Beweis enthalten, daß diese Kegelfunktionen durch einen höheren Typ von Hyperkegelfunktionen ersetzt werden müssen. Dies kam in dem sogenannten „Kepler-Problem“ zum Ausdruck, dessen Untersuchung Gauß die sogenannten elliptischen Transzendentalen entdecken ließ.
Das „Kepler-Problem“ entstand aus dem Versuch, die Bewegung eines Planeten in einem elliptischen Orbit zu bestimmen. Kepler hatte schon gezeigt, daß es unmöglich war, das dieser Bewegung zugrundliegende Prinzip mit Funktionen kreisförmiger Bewegung vollständig zu beschreiben. Die späteren Arbeiten von Leibniz bestätigten dies nicht nur, sondern zeigten zudem, daß auch die anderen Funktionen, die mit Kegelwirkungen zusammenhingen – hyperbolische und exponentielle – ungeeignet waren, die Bewegung eines Planeten in einem elliptischen Orbit zu beschreiben. Bereits 1797 erkannte Gauß, daß dies daher stammte, daß elliptische Bewegung durch elliptische Transzendentale bestimmt wird, welche eine andere und höhere Form als die einfachen kreisförmigen, exponentiellen und hyperbolischen Funktionen darstellten.
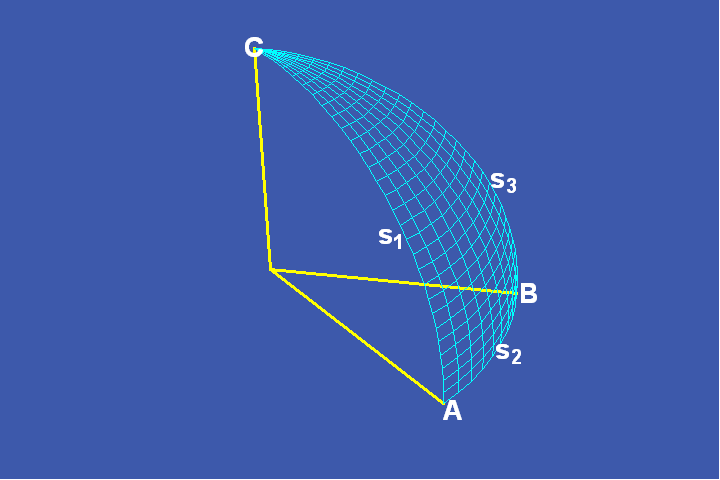
Später untersuchte Gauß die Beziehung zwischen diesen beiden transzendentalen Bereichen weiter. Eine seiner verblüffendsten Einsichten zeigte sich bei seiner Untersuchung des Pentagramma Mirificum. Das Pentagramma Mirificum war von John Napier, einem Zeitgenossen Keplers, in Verbindung mit seinen Untersuchungen über sphärische Trigonometrie entdeckt worden. Napier hatte erkannt, daß sich die selbstbegrenzende Natur der Kugel in der verbundenen Beziehung zwischen den Seiten und Winkeln eines sphärischen Dreiecks widerspiegelt. In einem solchen sphärischen Dreieck sind die Längen der Seiten eine Funktion der Winkel und umgekehrt. Im Spezialfall eines rechtwinkligen sphärischen Dreiecks zeigt sich dieses Verhältnis im Pentagramma Mirificum.
Anders als im euklidischen Dreieck, in welchem die Seiten als Längen gemessen werden, mißt man im sphärischen Dreieck sowohl die Seiten als auch die Winkel als Winkel (Abbildung 11).
Napier zeigte, daß in einem rechtwinkligen Kugeldreieck die drei Seiten und die beiden übrigen Winkel über eine Beziehung zwischen ihren Sinus und Kosinus miteinander zusammenhängen (Abbildung 12).
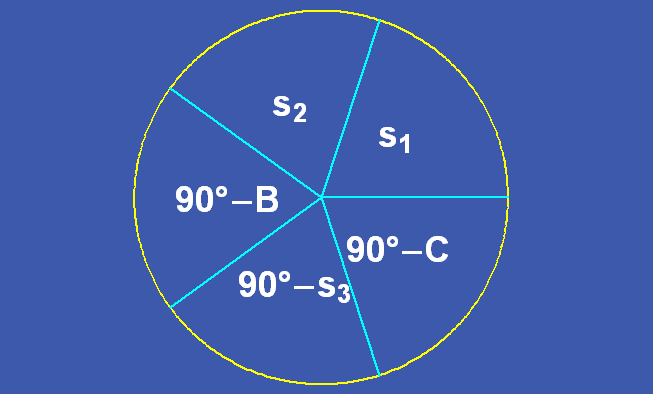
Zum Beispiel: sin s1 = tan s2 ∙ tan(90° – C) ; cos s1 = cos(90° – B) ∙ cos(90° – s3)
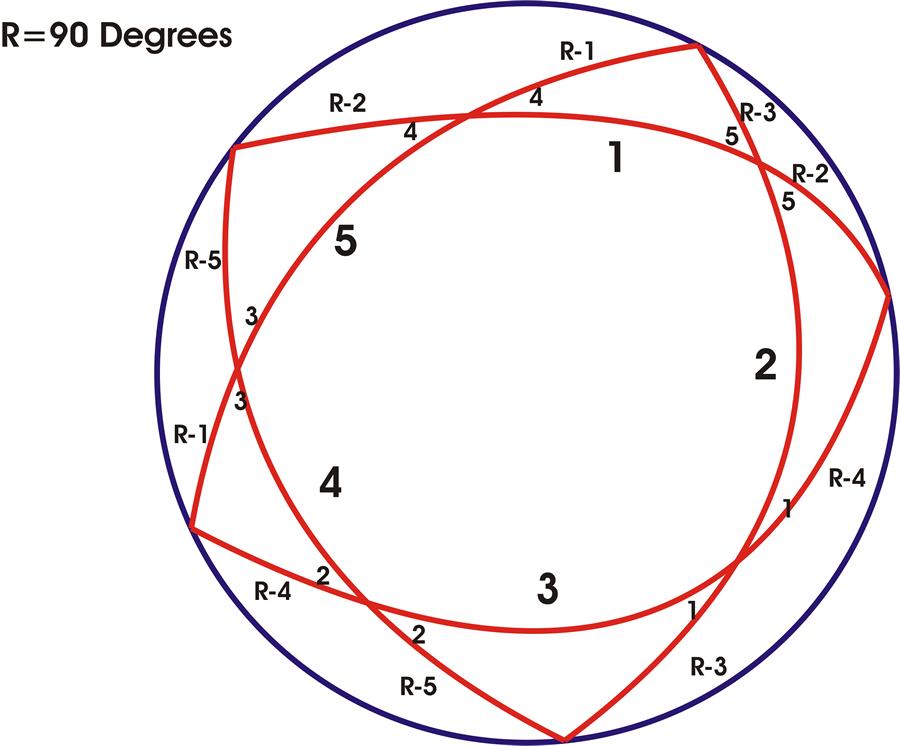
Die Beziehung zwischen diesen fünf Komponenten kann so geordnet werden, daß sie ein selbstpolares sphärisches Fünfeck bilden, das Napier das Pentagramma Mirificum nannte (Abbildung 13).
Gauß war von der Beziehung zwischen Napiers sphärischem Fünfeck und seinen elliptischen Transzendentalen fasziniert. Er erkannte aufgrund von Napiers Pentagramma Mirificum, daß eine Kugeloberfläche im Prinzip eine fünffache Periodizität besitzt. Und er sah diese fünffache Periodizität im Lichte der bekannten Entdeckung des Apollonius, daß fünf Punkte notwendig sind, um einen Kegelschnitt eindeutig zu bestimmen. Dies unterscheidet den allgemeinen Kegelschnitt von einem Kreis, der nur drei Punkte benötigt, und von einer Linie, die nur zwei Punkte benötigt. Gauß erkannte, daß die fünffache Periodizität der Kugel und die fünfpunktige Definition von Kegelschnitten den Unterschied zwischen der höheren Form von elliptischen Transzendentalen und der niederen Form der Transzendentalen, die mit Kreis-, Hyperbel- oder Exponentialfunktionen zusammenhängen, widerspiegelt.
Die einfachen Transzendentalen, wie sie bei Keplers Kegelfunktionen auftreten, entstehen in Verbindung mit physi scher Bewegung infolge eines einzigen Änderungsprinzips, wie zum Beispiel der Inkommensurabilität zwischen Bogen und Sinus bei gleichförmiger Kreisbewegung. Bei elliptischen Transzendentalen geht es aber, wie Gauß zeigte, um zwei Änderungsprinzipien, wie zum Beispiel bei einer Ellipse um die doppelte Inkommensurabilität zwischen Sinus und Bogen und Sinus und Winkel. Eine ähnliche elliptische Doppelinkommensurabilität tritt bei einem kreisförmigen Pendel zwischen Winkel und Sinus und Winkel und Zeit auf.
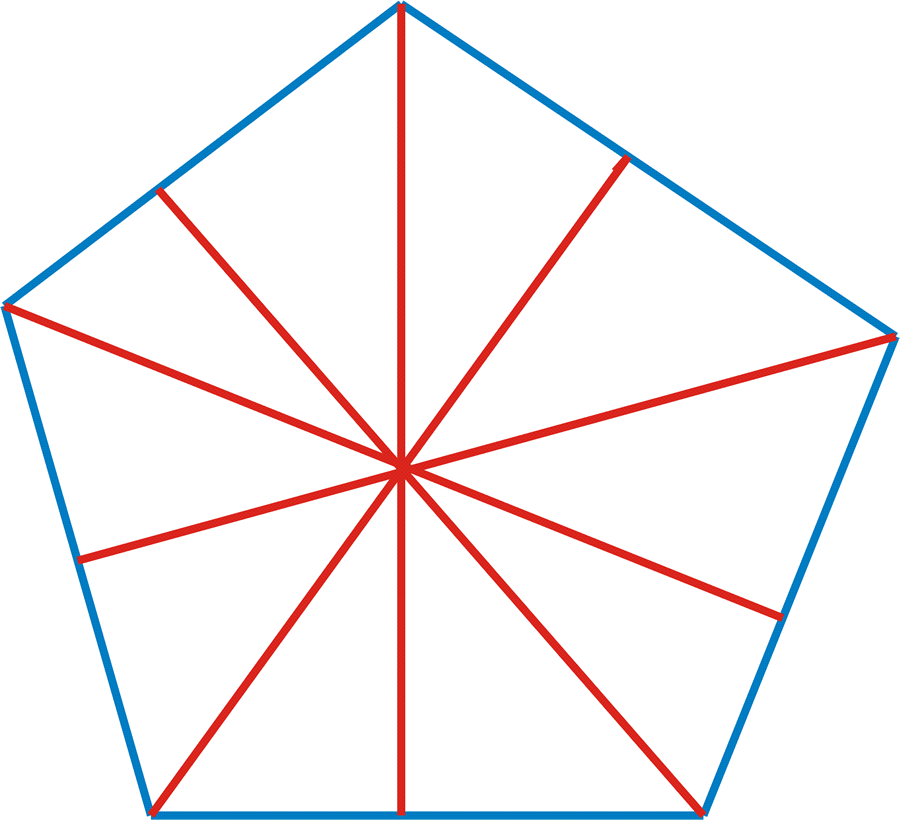
Die Verbindung zwischen dem sphärischen Fünfeck und den elliptischen Funktionen wird daran deutlich, daß, wie Gauß zeigte, ein geradliniges ebenes Fünfeck entsteht, wenn ein selbstpolares sphärisches Fünfeck durch einen Kegel, dessen Spitze im Zentrum der Kugel liegt, auf eine Tangentialebene der Kugel projiziert wird (Abbildung 14).
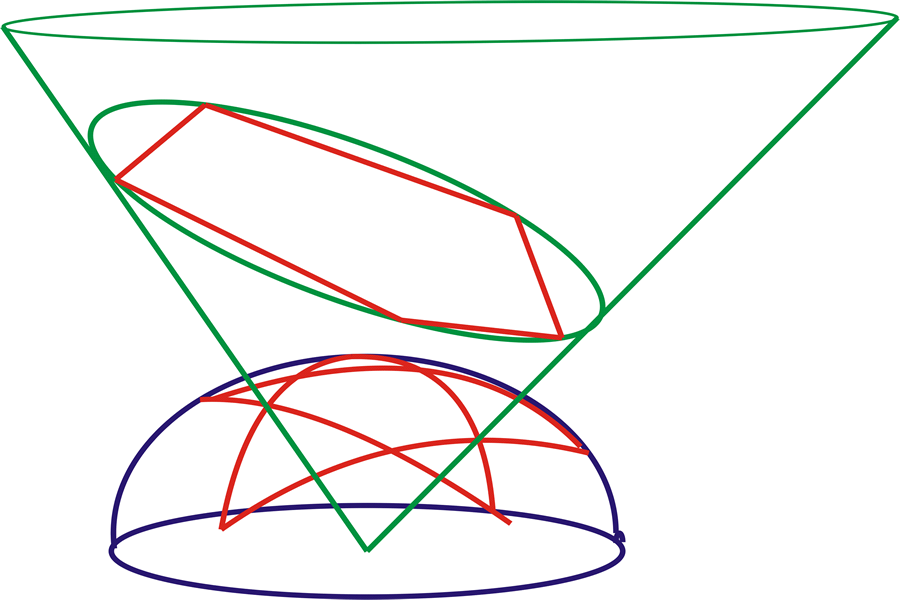
Die fünf Spitzen dieses ebenen Fünfecks definieren eine eindeutige Ellipse. Die Höhen dieses ebenen Fünfecks schneiden sich alle in einem Punkt, welcher ein Abbild des Berührungspunktes der Tangentialebene mit der Kugel ist (Abbildung 15).
Gauß zeigte, daß diese Eigenschaft Ausdruck der Tatsache ist, daß die Ecken und gegenüberliegenden Seiten des ebenen Fünfecks Abbilder der Pole und des Äquators des sphärischen selbstpolaren Fünfecks sind (Abbildung 16).
Dies ist eine Art „Dirichlet-Prinzip“ – nämlich die Höhenlinien des Kugelfünfecks können sich an jedem beliebigen Punkt innerhalb des Kugelfünfecks schneiden. Im ebenen Fünfeck gibt es aber nur eine Menge von Höhenlinien. Das heißt, das sphärische selbstpolare Fünfeck spiegelt eine ganze Mannigfaltigkeit ebener Fünfecke wider, wovon ein jedes elliptische Aktion darstellt. Die Be ziehungen zwischen diesen ebenen Fünfecken können nur durch eine elliptische Transzendentale ausgedrückt werden. Somit ist das sphärische
Pentagramma Mirificum die entfaltete Form einer elliptischen Funktion.
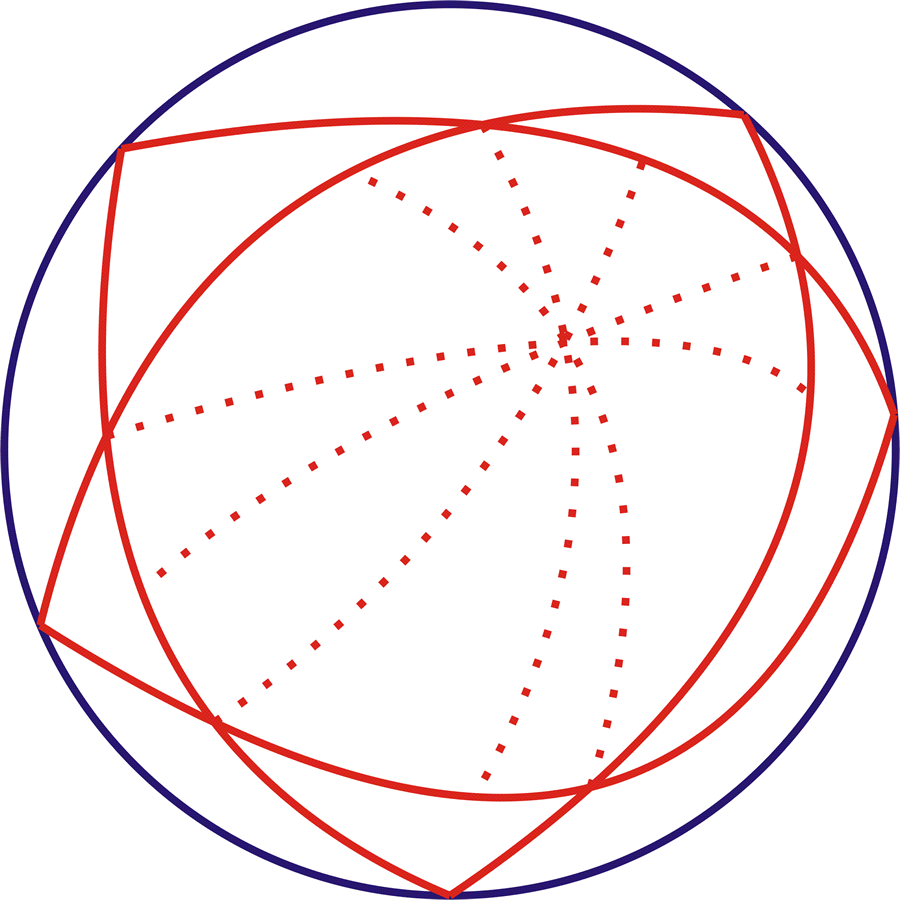
In seiner Arbeit über das Pentagramma Mirificum untersuchte Gauß dann dieses einer Ellipse einbeschriebene Fünfeck im Lichte von Keplers Positionsbestimmung eines Planeten auf einer elliptischen Bahn (Abbildung 17).
Er zeigte, daß die Beziehung zwischen dem sphärischen Fünfeck und dessen Projektion durch seine neue elliptische Transzendentale ausgedrückt wurde. Daraus wurde deutlich, daß die sphärische Aktion implizit elliptische Eigenschaften hat und nicht vollständig durch Kreisfunktionen ausgedrückt werden kann, wie aus der einfachen Sinneswahrnehmung geschlossen werden könnte. Da umgekehrt die Beobachtungen zeigten, daß die Planetenbahn elliptisch und nicht kreisförmig ist, wie Aristoteles dogmatisch behauptete, war es erforderlich, die naive Auffassung von einer Kugel zugunsten von höheren Erkenntnisformen abzulehnen, wie sie in Gauß’ und Riemanns hypergeometrischen Funktionen deutlich werden.
Der sich selbst entwickelnde Riemannsche Bereich
So wie Keplers Methode, angeregt durch die experimentell bestimmten elliptischen Bahnen, das Konzept einer nicht-unendlichen selbstbegrenzten Kegelfunktion erzeugte, so veranlaßte dieselbe Methode Gauß dazu, über Kepler hinaus zu gehen (wie Kepler selbst es gefordert hatte) und den Begriff einer höheren elliptischen Transzendentalen zu erzeugen. Solche elliptischen Transzendentalen sind jedoch ungeeignet, die höheren Formen physischer Aktion auszudrücken, welche Riemann als „vielfach zusammenhängende stetige Mannigfaltigkeiten“ bezeichnete. Eine geeignete Methode, diese Arten physischer Aktion zu verstehen, wurde erst erreicht, als Riemann die Gaußschen Arbeiten über hypergeometrische Funktionen vereinheitlichte und fortsetzte. Genauso wie Keplers elliptische Bahnen und ihre Untersuchung durch Gauß Konzepte von universeller Bedeutung hervorbrachten, produzierte Riemanns Untersuchung physischer Prozesse, die von hypergeometrischen Funktionen bestimmt werden, ein größeres Verständnis des Universums als Ganzem.
Dieses Konzept wurde in seiner Theorie der Abelschen Funktionen und in seinen Vorlesungen über Gaußens hypergeometrische Funktionen ausgearbeitet. Hier entwickelte Riemann die Mächtigkeit der Riemannschen Flächen, um so Konzepte darzustellen, die mit vielfach zusammenhängender hypergeometrischer Aktion verbunden sind. Da die Konstruktion von Riemannschen Flächen bereits in früheren Teilen dieser Serie dargestellt wurde, soll hier nur eine kurze Zusammenfassung folgen.
Riemann erkannte, daß die nicht-unendliche, selbstbegrenzte Mannigfaltigkeit, die bereits in Keplers Kegelfunktionen oder Desargues’ projektiver Geometrie angedeutet waren, der stereographischen Abbildung einer Ebene auf eine Kugelfläche entspricht. Diese „Riemannsche Kugel“ ist eine nicht-unendliche, selbstbegrenzte Fläche, deren Nordpol der Umschlagspunkt ist, welcher in der Ebene scheinbar im Unendlichen liegt. Projiziert man Keplers Kegelfunktion auf die Riemannsche Kugel, wird diese scheinbar unstetige Kegelfunktion zu einer stetigen Funktion. (Abbildung 18).
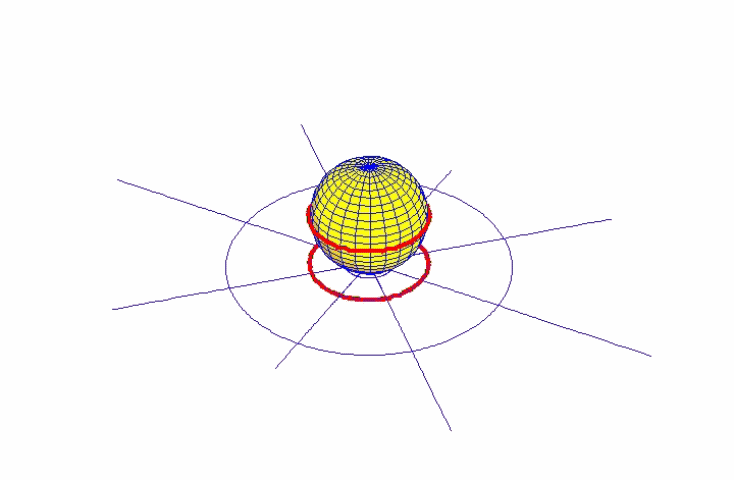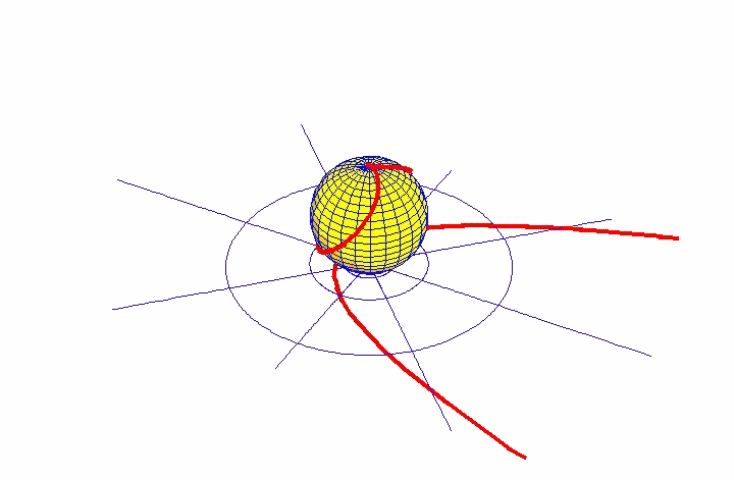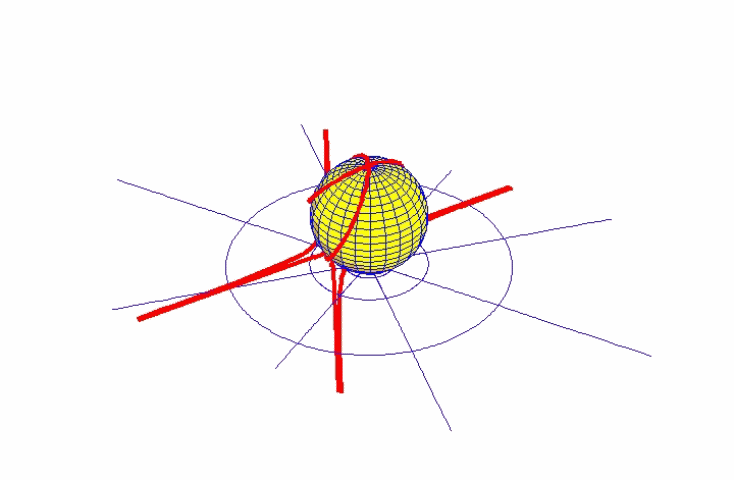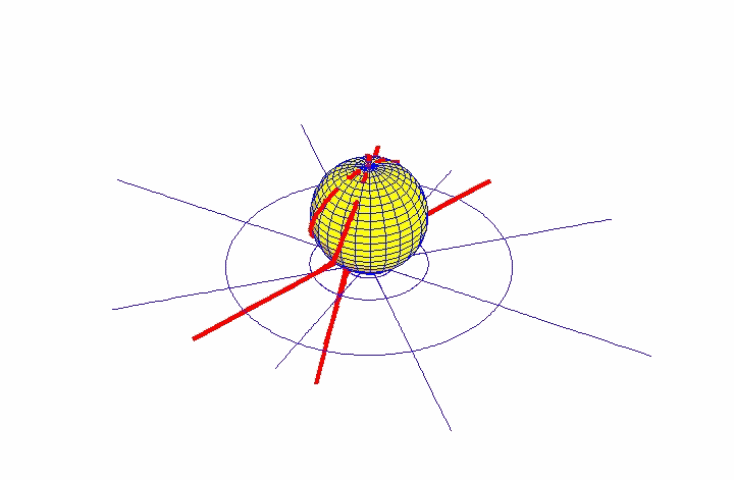
Die Unstetigkeit zwischen der elliptischen und der hyperbolischen Aktion bleibt zwar bestehen, aber auf der Riemannschen Kugel ist sie klar als singulärer Umschlagspunkt, nicht als eine mathematische Unendlichkeit vom euklidischen Typ dargestellt. Eine ähnliche Konstruktion kann man sich für Desargues’ vollständiges Viereck vorstellen.
Riemann zeigte, daß die einfach periodischen, kreisförmigen, hyperbolischen und exponentiellen Transzendentalen einer nicht-unendlichen, selbstbegrenzten Mannigfaltigkeit entsprechen, ausgedrückt durch eine Riemannsche Kugel.
Allerdings bewiesen Gauß, Jacobi, Abel und Riemann alle, daß die doppelt periodischen elliptischen Transzendentalen vier Punkte in der Unendlichkeit erzeugen.
Riemann betonte, daß eine nicht-unendliche, selbstbegrenzte Mannigfaltigkeit mit vier Unstetigkeiten nicht in Form einer Kugel dargestellt werden kann. Ihre geometrischen Charakteristiken entsprechen vielmehr der Gestalt eines Torus.
In seinen späteren Untersuchungen über die hyperelliptischen und Abelschen Funktionen zeigte Riemann, daß jede weitere Gradierung transzendentaler Funktionen eine steigende Anzahl von Unstetigkeiten enthält. Demzufolge ist eine steigende Anzahl von Unstetigkeiten mit einer Änderung in der Charakteristik („Genus“) der entsprechenden nicht-unendlichen, selbstbegrenzten Mannigfaltigkeit verbunden (Abbildung 19).

Die geometrische Darstellung von Änderungen zwischen Mannigfaltigkeiten verschiedener Genera stimmt mit dem topologischen Unterschied zwischen einer Kugel und einem Torus überein. Diese topologische Verschiedenheit drückt sich in der Fähigkeit der Mannigfaltigkeit aus, eine größere Anzahl unterschiedlicher Aktionswege zuzulassen. Das heißt, jede weitere Art nicht-unendlicher, selbstbegrenzter Mannigfaltigkeiten ist in der Lage, eine physische Aktion von immer größerer Komplexität auszudrücken.
Aber genauso wie Keplers Kegelschnitte von einem projektiven Standpunkt aus die zugrundeliegende epistemologische Bedeutung elliptischer Bewegung offenbart, so eröffnet auch erst die projektive Sicht dieser Abfolge selbstbegrenzter Riemannscher Mannigfaltigkeiten deren wirkliche Schönheit.
Gehen wir vom einfachsten Fall aus, der selbstbegrenzten sphärischen Mannigfaltigkeit. Die Projektion dieser Mannigfaltigkeit drückt sich durch Keplers und Desargues’ projektive Beziehung aus. Nun der nächste Fall: der selbstbegrenzte Torus in Verbindung mit den elliptischen Transzendentalen. Seine projektive Form ist ein Parallelogramm mit vier anscheinend unendlichen Größen (Abbildung 20).
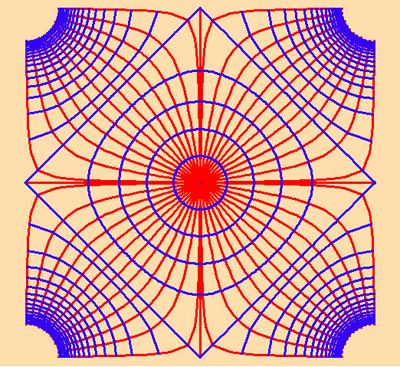
Man betrachte diese Mannigfaltigkeit, wie Riemann, als eine Mannigfaltigkeit des physischen Potentials. In dieser Hinsicht werden die Beziehungen zwischen den rechtwinkligen Pfaden minimaler und maximaler Potentialänderungen durch die vier scheinbar unendlichen Größen bestimmt. Genau wie der „Fernpunkt“ zum Beispiel die harmonischen Eigenschaften des vollständigen Vierecks bestimmt, so bestimmen die vier „Fernpunkte“ einer elliptischen Transzendentalen die harmonischen Eigenschaften dieser Mannigfaltigkeit. Dies drückt sich zum Beispiel dadurch aus, daß sich die Potentialeigenschaften von einer kreisförmigen Begrenzung in der Nähe des Zentrums der Mannigfaltigkeit in eine quadratische Begrenzung in Richtung der Ecken verwandelt.
Dennoch darf man die scheinbar unendlichen Größen in den elliptischen Transzendentalen nicht als „Unendlichkeiten“ auffassen, sondern als Unstetigkeiten innerhalb eines ansonsten selbst- begrenzten stetigen Prozesses. Mit anderen Worten, genauso wie Keplers Kegelfunktion die scheinbar unendliche Grenze zwischen dem Elliptischen und dem Hyperbolischen in eine Unstetigkeit innerhalb einer ansonsten stetigen, selbst- begrenzten Mannigfaltigkeit transformierte, muß ein ähnliches Mittel „zur Fortsetzung jenseits des Unendlichen“ für die elliptischen Transzendentalen gefunden werden.
Hierzu benutzte Riemann die Entdeckung eines anderen Gauß-Schülers, Ferdinand Möbius, der Gauß’ Abhandlung über komplexe Funktionen weiterführte. Möbius untersuchte die Eigenschaften des scheinbar einfachsten Typus komplexer Funktionen: einfache lineare Transformationen der Form
(a ∙ z + b)/(c ∙ z + d) ,
wobei z eine Variable und a, b, c, d beliebige komplexe Zahlen sind. Diese Möbius-Transformationen spielen für die höheren transzendentalen Funktionen eine ähnliche Rolle wie die Exponentialfunktionen im Hinblick auf Leibniz’ Kettenlinie und die einfachen Transzendentalen.
Beispiele für einfache Transformationen sind Translation, Inversion, Rotation und Kombinationen von allen dreien (siehe Abbildungen 21 a–f).
Möbius entdeckte, daß diese einfachen Typen komplexer Transformationen eigentlich Verallgemeinerungen von Keplers und Desargues’ projektiver Geometrie sind. Unter diesen Möbius-Transformationen ist das Doppelverhältnis vier beliebiger komplexer Zahlen invariant. Wenn das Doppelverhältnis eine nicht-komplexe Zahl ist, liegen die vier Punkte entweder auf einem Kreis oder auf einer Linie. Um bei Cusa zu bleiben, muß eine Linie als ein Kreis angesehen werden, dessen Mittelpunkt „im Unendlichen“ liegt.
Es läßt sich immer eine eindeutige Möbius-Transformation finden, die beliebige drei Punkte auf null, eins und unendlich abbildet. Das heißt, es ist geometrisch sehr einfach, in bezug auf Möbius- Transformationen das Doppelverhältnis zu definieren, wenn drei der Punkte, die das Doppelverhältnis bilden, null, eins und unendlich sind. Auf einer Riemannschen Kugel heißt das, daß die Punkte den Südpol, den Nordpol und den Äquator bilden (Abbildung 22).
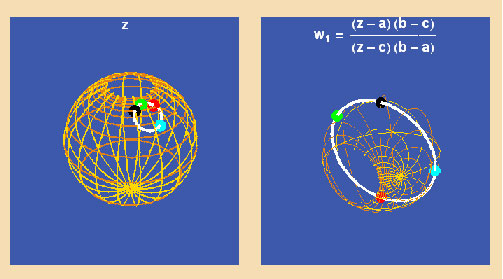
Bei elliptischen Transzendentalen gibt es jedoch vier Punkte, die im Unendlichen, und vier Punkte, die in Eins abgebildet werden. Dennoch führt eine einfache Reihe von Möbius-Transformationen diese Projektionen jenseits des Unendlichen fort (Abbildung 23).
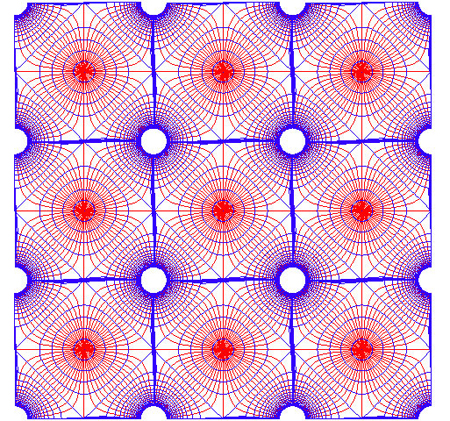
Daraus ergibt sich das projizierte Bild eines selbstbegrenzten Torus mit einer größeren Dichte von Unstetigkeiten, als dies in einer sphärischen Mannigfaltigkeit möglich ist (siehe Abbildungen 24 a, b).


Bei der Hyperellipse ist das projizierte Bild der Riemannschen Fläche eine Art Achteck mit acht „Fernpunkten“ und acht Punkten, die auf die Eins abgebildet werden. Wie bei den elliptischen Funktionen bestimmen diese acht Fernpunkte die harmonische Charakteristik der Mannigfaltigkeit, aber anders als bei der Ellipse sind acht Fernpunkte mit einem Wechsel zu negativer Krümmung verbunden. Eine andere Art von Möbius-Transformation setzt diese Projektion über das Unendliche fort. Das heißt, die hyperelliptische Funktion kann nur in einer negativ gekrümmten, nicht-unendlichen, selbstbegrenzten Mannigfaltigkeit existieren.
Eine solche Mannigfaltigkeit läßt sich nicht vollständig im sichtbaren Raum darstellen. Daher können wir eine solche Mannigfaltigkeit nur als Projektion auf die Höhlenwand der sinnlichen Wahrnehmung „beobachten“.
Dennoch ist es wichtig, die Bedeutung des Wechsels in der charakteristischen Krümmung zwischen Ellipse und Hyperellipse zu betonen. Das Kennzeichen sphärischer Mannigfaltigkeiten ist die positive Krümmung. Der Torus kombiniert positive und negative Krümmung zu einer Gesamtkrümmung von null. Die selbstbegrenzten Mannigfaltigkeiten der Hyperellipse und jenseits davon werden durch negative Krümmung charakterisiert.
Von diesem Standpunkt aus erscheint die Unstetigkeit, die in Keplers Kegelfunktion zwischen dem elliptischen und dem hyperbolischen Bereich auftritt, in einem neuen Licht. Sie entspricht dem Wechsel der Charakteristik zwischen den im allgemeinen positiv gekrümmten Mannigfaltigkeiten der einfachen und elliptischen Transzendentalen zu den negativ gekrümmten Mannigfaltigkeiten der hyperelliptischen (hyperbolischen) Art.
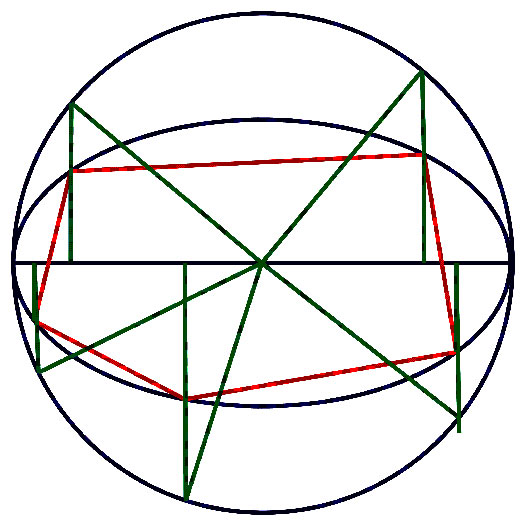
Riemann erkannte die Bedeutung dieses Wechsels und war überzeugt, daß nur ein Raumbegriff, der alle drei Krümmungstypen umfaßt, universelle Prinzipien geeignet repräsentieren könne. In seiner Habilitationsschrift schlug er als Bild für eine solche Mannigfaltigkeit die zusammentreffenden Flächen von Kugel, Zylinder und dem negativ gekrümmten inneren Teil eines Torus vor (Abbildung 25).
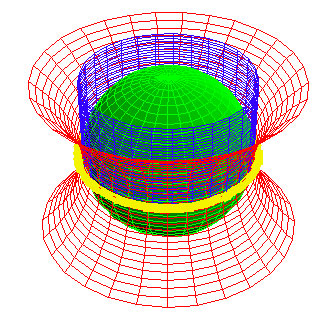
Alle drei Flächen werden von einem Kreis umfaßt, der das Bild des sichtbaren Raumes darstellt.
Auch hier existiert die euklidische Ebene ohne Krümmung nur im Geist von Aristotelikern und Narren. Sie ist nur die begrenzte Sicht einer Mannigfaltigkeit, die positiv wie negativ gekrümmt ist. Eine Mannigfaltigkeit, wie sie durch den Torus der Riemannschen Flächen oder metaphorisch durch den Zylinder in der obigen Konstruktion dargestellt wird, ist lediglich ein Übergang zwischen dem überwiegend positiv gekrümmten Bereich des sichtbaren Raumes und dem überwiegend negativ gekrümmten Bereich des sehr Großen und sehr Kleinen.
Das heißt, das Universum läßt sich nicht durch eine einzige Krümmungsart kennzeichnen. Vielmehr muß es als dynamischer Prozeß gedacht werden, in dem alle drei Krümmungstypen wechselwirken.
Auf diese Weise entsteht aus Riemanns Abhandlung der Abelschen und hypergeometrischen Funktionen ein Konzept, das nicht in einer einzigen nicht-unendlichen, selbstbegrenzten Mannigfaltigkeit, sondern in einer verschachtelten Folge solcher Mannigfaltigkeiten besteht, einer Art Mannigfaltigkeit von Mannigfaltigkeiten. Solch eine Mannigfaltigkeit von Mannigfaltigkeiten – welche in Riemanns Darstellung mit einer einfachen selbstbegrenzten Kugel anfängt, weiter zum Torus und dann zu den hyperelliptischen und höheren Funktionen führt – läßt eine Vorstellung über die Form eines nicht-unendlichen, sich selbst entwickelnden, selbst- begrenzten Universums entstehen.
Ein letzter Blick auf Kepler, Riemann und Einstein
Einstein beendete seine Schrift über Kepler 1930 so:
„Es scheint, daß die menschliche Vernunft die Formen erst selbständig konstruieren muß, ehe wir sie in den Dingen nachweisen können. Aus Keplers wunderbarem Lebenswerk erkennen wir besonders schön, daß aus bloßer Empirie allein die Erkenntnis nicht erblühen kann, sondern aus dem Vergleich des Gedachten mit dem Beobachteten.“
Diese Schlußworte machen Einsteins Ablehnung des Positivismus deutlich und lassen, wenn auch in abgeschwächter Form, auf den Einfluß von Kepler und Riemann auf sein Denken schließen. Doch sie verdeutlichen auch sein Scheitern. Fortschritt in der Wissenschaft hängt vom Aufbau einer starken Bindung an Kepler und Riemann ab. Der menschliche Geist konstruiert nicht erst unabhängig Formen, bevor er sie in den Dingen findet, denn er ist nie unabhängig von dem Universum, in dem er existiert. Die Wechselwirkung des Geistes mit den beobachteten Fakten ist keine Wechselwirkung zweier getrennter Bereiche. Sie ist eine Wechselwirkung, die die sich selbst entwickelnden, vielfach zusammenhängenden Bereiche der Physik, das Lebens und das Denkens verändert.
Keplers wunderbare Errungenschaften sind ein schönes Beispiel für diese Art des Denkens. Heute ist mehr als bloße Bewunderung für Kepler nötig. Wir brauchen eine ganze Armee von neuen Keplers, die mit Hilfe von Riemanns Konzepten und LaRouches Entdeckungen das tun, was Kepler während des kurzen Zeitabschnitts getan hat, der vor 375 Jahren endete: die sich in der Natur stellenden Paradoxe aufgreifen und in ihnen ein tieferes Verständnis der menschlichen Natur finden.
