Was mich anbetrifft, so schätze ich die Mathematik nur, weil ich darin die Spuren der Erfindungskunst im allgemeinen wiederfinde, und mir scheint, ich habe am Ende entdeckt, daß selbst Descartes nicht in das Geheimnis dieser großen Wissenschaft eingedrungen ist. Ich erinnere mich, daß er einmal gesagt hat, die Vorzüglichkeit seiner Methode, die bloß in seiner Physik glaubhaft erscheine, werde in seiner Geometrie bewiesen. Aber ich muß sagen, daß ich gerade in Descartes‘ Geometrie die prinzipielle Unvollkommenheit seiner Methode erkannt habe… Ich behaupte, es gibt eine vollkommen andere Methode der geometrischen Analyse als die von Vieta und Descartes [d. h. Algebra, Anm d. Verf.], die nicht weit genug gingen, weil die wichtigsten Probleme überhaupt nicht von den Gleichungen abhängen, auf die Descartes seine Geometrie reduziert.
Eines der berühmtesten Probleme der antiken Geometrie war die Aufgabe, die Seitenlänge eines Würfels zu konstruieren, dessen Volumen genau dem doppelten Volumen eines gegeben Würfels entspricht. Interessanterweise läßt sich diese Aufgabe nicht mit Hilfe von Zirkel und Lineal allein, d. h. nicht mit den gewöhnlichen Konstruktionsmitteln der Geometrie lösen. Die Lösung erfordert andere Mittel, sprengt damit den Rahmen der einfachen Euklidischen Geometrie und zeigt die Notwendigkeit einer anderen, höheren physikalischen Geometrie, die nicht auf aprioristische, formallogische Weise wie die Euklidische oder später die algebraische Geometrie von Descartes, sondern aus der experimentellen Entdeckung neuer physikalischen Prinzipien abgeleitet wird.
Unter den verschiedenen klassischen Lösungen für die Verdoppelung eines Würfels ist jene des platonischen Philosophen und Mathematikers Archytas besonders lehrreich. Nach Archytas wird die gesuchte Seitenlänge an Hand des Schnittpunktes dreier Flächen erzeugt: eines Torus, eines Zylinders und eines Kegels. Jede dieser Flächen wird wiederum durch die Rotation als Wirkungsprinzip erzeugt. Mit seiner Arbeit nahm Archytas die spätere Entwicklung der physikalischen Geometrie durch Leonardo, Kepler, Leibniz, Gauß und Riemann vorweg.
Betrachtet man sich aber jüngste Darstellungen jener berühmten Konstruktion, so wird deutlich, wie tief die heutige Mathematik unter das Denken der Kreise um Platon vor über 2.300 Jahren zurückgefallen ist. Typisch hierfür ist eine Darstellung der Verdoppelung des Würfels auf einer Internetseite von J. J. O’Connor und E. F. Robertson. Der Text enthält zwar einige interessante Zitate und Verweise, aber wenn die Autoren die tatsächliche Konstruktion des Archytas behandeln, verfallen sie in simple Schuljungenweisheiten: „Versuchen wir doch einfach, mit der üblichen Koordinatengeometrie nachzuprüfen, ob Archytas recht hat!“ Im Rahmen eines kartesischen Koordinatensystems schreiben sie für jede der drei Flächen (Kegel, Zylinder und Torus) algebraische Gleichungen in x, y, z auf und kombinieren die Gleichungen, um zu zeigen, daß die gewünschten Proportionalitäten „irgendwie herauskommen“. Magie! Wer sich solchen formalen Übungen unterzieht, wird nicht nur weniger als nichts über Archytas‘ tatsächliche Entdeckung gelernt haben, schlimmer noch, die kognitiven Denkprozesse werden insgesamt abgeschaltet worden sein.
Angesichts der erstaunlichen Reichweite von Archytas‘ synthetisch-geometrischem Ansatz wird deutlich, daß die gängigen Darstellungen der antiken griechischen Mathematik völlig unzureichend sind und daß die tatsächlichen physikalischen Konzepte seiner Arbeit unterdrückt wurden. Bekanntlich sind die meisten der wichtigsten Originaldokumente der griechischen Wissenschaft verloren gegangen, und die lebende Kontinuität der griechischen Wissenschaft brach im Zuge des vom Römischen Reich erzwungenen „finsteren Zeitalters“ ab. Auf diese Weise wurde die erhalten gebliebene Version von Euklids berühmten Elementen – eine Sammlung, deren axiomatisch-deduktive Darstellungsweise die wesentlichen Ideen und historischen Entwicklungsprozesse der griechischen Wissenschaft unterdrückt – zur nahezu ausschließlichen Quelle für die klassische griechische Geometrie sowie seit vielen Jahrhunderten zur Grundlage des elementaren Mathematikunterrichts. So wird in Euklids Elementen u. a. die natürliche Entwicklungsordnung selbst in der visuellen Geometrie umgeworfen, indem die ebene Geometrie und die angeblich selbstevidenten Begriffe von „Punkt“ und „Gerade“ als nicht weiter zerlegbare Einheiten an den Anfang gestellt werden und erst in den Schlußkapiteln zu den Konstruktionen der Stereometrie (d. h. der dreidimensionalen Geometrie) übergegangen wird. Hingegen ist die erste und elementarste visuelle Geometrie keineswegs „eben“, sondern sphärisch – entsprechend jener Geometrie, die auf die Astronomie als die älteste menschliche Wissenschaft zurückgeht.
Aus diesen und ähnlichen Umständen wird erklärlich, warum die größten wissenschaftlichen Denker von der Renaissance bis Kepler und Leibniz einen Großteil ihrer Bemühungen darauf verwandten, die wirkliche Methode und „Seele“ der klassischen griechischen Mathematik wiederherzustellen, so wie sie bestenfalls „zwischen den Zeilen“ der euklidischen und anderer, meist fragmentarisch überlieferter Texte gelesen werden konnte. Die überlieferten Platon-Dialoge waren hierfür der allerwichtigste Referenzpunkt.
Entscheidend hierfür war, daß in der Renaissance das isoperimetrische Prinzip der Kreis- und Kugelgeometrie sowie die Bedeutung der fünf regelmäßigen Körper wiederbelebt wurden. Bahnbrechend war, wie es Pacioli und Leonardo da Vinci in ihrem berühmten Buch über die „göttlichen Proportion“ gelang, Euklid gewissermaßen „auf den Kopf“ zu stellen, indem sie Euklids berühmtes 13. Buch an die erste Stelle stellten. Kepler führte die Polemik noch weiter, indem er vom Standpunkt der entscheidenden Rolle der regelmäßigen Körper eine erste Annäherung an eine wirkliche physikalische Geometrie entwickelte. Dies führte direkt zu Fermats, Pascals und Leibniz‘ Neubearbeitung von Fragen wie Apollonios‘ Abhandlung über Kegelschnitte, wobei die Vorstellung höher geordneter, mehrfach zusammenhängender Mannigfaltigkeiten immer mehr in Mittelpunkt rückte, worum sich offenbar auch die Diskussionen unter Platons Wissenschaftskollegen drehten. Somit verläuft eine direkte Linie von Archytas und Apollonios zu den Arbeiten von Gauß und Riemann.
Von dieser Sicht empfehle ich allen, die sich in diese Materie vertiefen wollen, die folgenden Beobachtungen über Archytas‘ Konstruktion der Verdoppelung des Würfels. Die Darstellung ist zwar etwas technisch und soll auch keineswegs seine gesamte Entdeckung beleuchten, aber zumindest kann sie eine fruchtbare Diskussion in Gang setzen und einige der Schäden der heutigen verzerrten Sichtweise reparieren.
Mittlere Proportionalen und die Verdoppelung des Würfels
Im Anschluß an die Entdeckung des Hippokrates von Chios näherte sich Archytas dem Problem der Würfelverdoppelung, indem er das allgemeine Problem der Konstruktion zweier „mittlerer Proportionalen“ zwischen den gegebenen Längen a und b löste.
Zur kurzen Erläuterung: Unter „zwei mittleren Proportionalen“ versteht man zwei Größen x und y zwischen zwei gegebenen Größen a und b (wobei a größer sein soll als b), so daß b : x = x : y = y : a. Die Verdoppelung des Würfels entspricht hierbei dem Sonderfall a = 2 und b = 1.Das erste der beiden geometrischen Mittel, x, entspricht der Seite eines Würfels mit der doppelten Fläche des Ausgangswürfels. Das zwei Mittel, y, entspricht der Fläche einer Seite des neuen Würfels.
Um zu verstehen, woher das doppelte Mittel kommt, stelle man sich einen Einheitswürfel vor, der durch folgenden Prozeß in einen doppelt so großen Würfel verwandelt wird. Zuerst „ziehe“ man den Würfel an seiner Breite (d. h. horizontal), ohne seine Tiefe und Höhe zu verändern, so daß seine Breite gleich x (der Seitenlänge des Doppelwürfels) wird. Hierdurch vergrößert sich sein Volumen um einen Faktor x im Verhältnis zu dem Ausgangsvolumen. Nun strecke man den Körper um den gleichen Faktor in der Tiefe, wobei die Breite gleich x und die Höhe gleich 1 bleibt. Schließlich strecke man den Körper in der Höhe um den Faktor x, wobei Breite und Tiefe gleich x bleiben. Daraus ergibt sich ein Würfel der Seitenlänge x – d. h. ein Würfel mit doppeltem Volumen.
Da jede dieser drei Transformationen das Volumen um den gleichen Faktor erhöht, steht jedes Volumen zu dem vorherigen jeweils im gleichen Verhältnis (nämlich x). Da das Ausgangsvolumen 1 und das Endvolumen 2 ist, bilden die Zwischenvolumina N und M eine Reihe geometrischer Mittel 1 : N = N : M = M : 2. Da jede der beschriebenen Streckungen das Volumen um einen Faktor x erhöht, gilt:
N = x · 1 = x
und
M = x · N = x2
Daraus ergibt sich die folgende Proportion:
1 : x = x : x2= x2 : 2 .
Die Seitenlänge x des Doppelwürfels ist also die erste der zwei mittleren Proportionalen zwischen 1 und 2.
Die Geometrie physikalischer Ereignisse
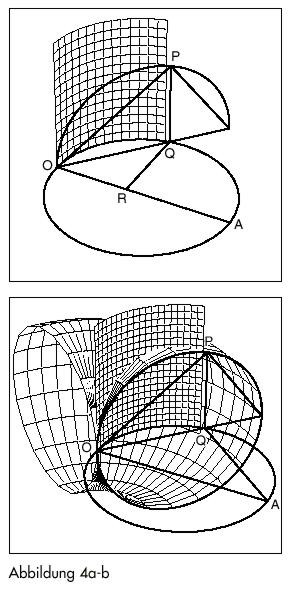
Man beachte vor allem: Indem Archytas die zwei mittleren Proportionalen durch den Schnitt zwischen einem Torus, Kegel und Zylinder ableitet, behandelt er das Problem ausdrücklich im Bereich der mehrfach zusammenhängenden, „polyphonen“ Kreiswirkung. In der klassischen Darstellung von Archytas‘ Konstruktion durch den Geometer Eudemus kommt vor allem der Idee der Bewegung und Erzeugung eine große Bedeutung zu:
„Zwei gegebene Linien seien OA [= a] und b; es ist erforderlich, zwei Mittel zwischen a und b zu konstruieren. Man schlage den Kreis mit OA als Durchmesser, wobei OA der größere Teil [der beiden] ist, und beschreibe OB [als Sehne an den Kreis] mit der Länge b ein und verlängere sie, damit sie bei C die an den Kreis bei A gelegte Tangente trifft… Man stelle sich einen Halbzylinder vor, der sich auf dem Halbkreis OBA senkrecht erhebt, und daß weiter auf OA ein senkrechter Halbkreis aufgerichtet wird, der auf [der Basis] des Halbzylinders steht. Wenn man diesen Halbkreis von A nach B bewegt, wobei der Endpunkt O des Durchmessers fest bleibt, schneidet er bei seiner Bewegung die Zylinderfläche und zeichnet darauf eine bestimmte Kurve. Wenn dann OA fest bleibt und wenn sich das Dreieck OCA mit einer Bewegung entgegen der des Halbkreises um OA dreht, erzeugt es eine Kegelfläche mit Hilfe der Linie OC, die im Laufe ihrer Bewegung die auf den Zylinder gezeichnete Kurve an einem bestimmten Punkt P trifft…“
P und seine Projektion R auf die horizontale Ebene liefern die gesuchten Mittel zwischen a und b; wie wir unten zeigen werden, gilt die doppelte Proportion: b : OR = OR : OP = OP : a. In Falle a = 2, b = 1 entspricht OR der Seitenlänge jenes Würfels, dessen Volumen genau das Doppelte des Einheitswürfels ist.
Was für ein Gegensatz zwischen dem polyphonen Geometriekonzept von Archytas und der heutigen geisttötenden „Mengenlehre“! In Archytas‘ Konstruktion entsteht P nicht als „Schnittmenge“ statischer „Punktmengen“, sondern als Ort eines physischen Ereignisses, dessen Erzeugungsprozeß drei (bzw. sogar sechs) gleichzeitige Aktionsgrade beinhaltet. Archytas plante den Prozeß auf eine Weise, daß das so erzeugte Ereignis genau die erforderlichen Beziehungen besitzt.
Bevor wir versuchen wollen, Archytas‘ Konstruktion selbst herzuleiten, wollen wir uns mit der einfacheren Frage der Beziehung zwischen geometrischem Mittel und Kreisprozeß beschäftigen.
Harmonische Proportionen und Kreisprozeß
Mit Hilfe der Kreisdrehung lassen sich auf einfachste Weise harmonische Proportionen zwischen scheinbar skalaren Größen (Linienabschnitte beispielsweise) als „projiziertes“ Ergebnis eines Vorgangs höherer Ordnung erzeugen.
Man konstruiere einen Kreis mit einem gegebenen Durchmesser OA. Ein Punkt P, der sich zwischen O und A auf dem Kreis entlangbewegt, läßt harmonische Proportionen kontinuierlich entstehen (Abbildung 1 a–c).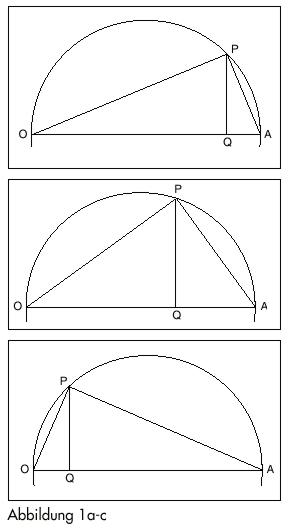
Verbindet man P mit den Endpunkten des Durchmessers O und A, entsteht ein Dreieck OPA, dessen Gestalt sich mit der Position von P ändert, dessen Winkel bei P aber immer ein rechter ist. Projizieren wir nun P senkrecht zur Linie OA und nennen den Projektionspunkt Q. Das Dreieck OPQ ist offenbar auch ein rechtwinkliges Dreieck (mit dem rechten Winkel bei Q), und es hat bei O einen gemeinsamen Winkel mit dem rechtwinkligen Dreieck OPA. Die beiden Dreiecke sind somit bei der gesamten Bewegung von P beständig ähnlich, und die entsprechenden Seitenverhältnisse sind gleich, besonders OQ : OP = OP : OA .
Die Strecke OP stellt also das geometrische Mittel zwischen OQ und OA dar. Durch Umkehr der Konstruktionsanordnung kann man mit Hilfe des Kreises das geometrische Mittel jeder beliebigen Längen OQ und OA erzeugen. Man fälle nur das Lot von Q auf den Kreisumfang, um den Punkt P zu erhalten.
Das geometrische Mittel war im antiken Griechenland auch als „einzelnes Mittel zwischen zwei Extremen“ bekannt. Zur Verdoppelung eines Quadrats muß ein solches einzelnes (geometrisches) Mittel zwischen 1 und 2 konstruiert werden. Um einen Würfel zu verdoppeln, braucht man jedoch zwei Mittel zwischen 1 und 2, oder, anders gesagt, eine Reihe gleichzeitiger Proportionen der Form
1 : OQ = OQ : OP = OP : 2
Die eben beschriebene Kreiskonstruktion, angewendet auf einen Kreis mit dem Radius OA = 2, erzeugt bereits die „Hälfte“ der gewünschten Proportion, nämlich OQ : OP = OP : 2 .
Denkt man darüber nach, bietet sich die folgende Strategie für die Verdopplung des Würfels an: Man führe einen zweiten Rotationsgrad aus, um die „andere Hälfte“ der Doppelproportion zu erzeugen, nämlich:
1 : OQ = OQ : OP
Man müßte dazu lediglich die beiden Kreisprozesse irgendwie miteinander kombinieren, um ein Ereignis zu erzeugen, an dem beide Bedingungen gleichzeitig verwirklicht werden. Daraus ergäbe sich das gewünschte doppelte Mittel: 1 : OQ = OQ : OP und gleichzeitig OQ : OP = OP : 2 .
Verfolgt man diese Strategie, kommt man zwar zu einer Konstruktion des doppelten Mittels, aber daran läßt sich bestimmte Kritik üben. Ich stelle sie kurz dar, da sie bereits in die Richtung eines „polyphonen“ Prozesses weist.
Ein vorläufiger Vorstoß
Um die Proportion 1 : OQ = OQ : OP in der genannten Weise zu erhalten, braucht man einen zweiten Kreis mit dem Durchmesser OP, und die folgenden Bedingungen müssen erfüllt sein (Abbildung 2 a–c):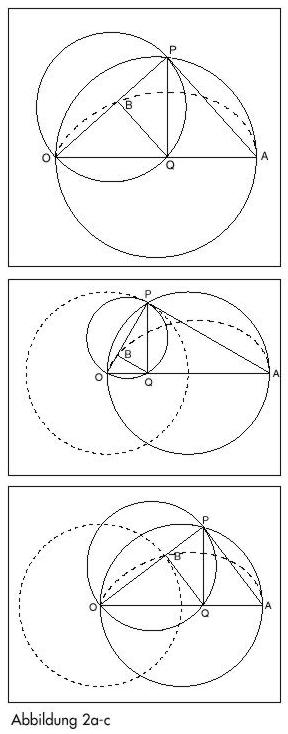
- der Punkt Q (die Projektion von P auf den Durchmesser des ersten Kreises) liegt ebenfalls auf dem zweiten Kreis, und
- Q projiziert sich auf einen Punkt B auf dem Durchmesser OP des zweiten Kreises, wobei die Strecke OB die Länge 1 haben muß.
Mit ein wenig Geometrie läßt sich zeigen, daß Bedingung 1 für alle Positionen von P auf dem ersten Kreis erfüllt ist; Bedingung 2 ist jedoch nur für eine Position von P (und sein symmetrisches Abbild) erfüllt. Wie läßt sich dieser Ort als konstruierbares Ereignis erzeugen?
Im Prinzip ganz einfach! Man vergegenwärtige sich, daß für jede Position von P bei dessen Bewegung entlang des ersten Kreises ein entsprechender Kreis um OP als Durchmesser konstruiert wird. Bei diesem Prozeß entsteht eine kontinuierliche Familie von Kreisen, deren Durchmesser OP sich mit jeder Bewegung von P winkel- und längenmäßig ändern.2 Für jeden dieser Kreise erzeuge man die entsprechenden Punkte Q und B, wie oben unter 1. und 2. angedeutet. Wenn P den Umfang des ersten Kreises umwandert, durchläuft der Punkt B eine bestimmte Kurve im Inneren des Kreises. Nun trage man einen dritten Kreis mit dem Radius 1 um den Punkt O ein. Leicht läßt sich sehen, daß die von B gezeichnete Kurve den dritten Kreis an einem bestimmten Punkt schneidet. An diesem Punkt (OB = 1) sind die Bedingungen 1 und 2 erfüllt, und für die entsprechenden Positionen P und Q gilt die gewünschte Proportion 1 : OQ = OQ : OP . Zusammen mit der Proportion OQ : OP = OP : 2 ergeben sich damit OQ und OP als die beiden mittleren Proportionalen zwischen 1 und 2. Das Problem ist gelöst!
Man könnte hier jedoch mit einigem Recht einwenden, daß damit keine wirkliche Methode aufgezeigt wurde, wie die als Ort der Punkte B definierte Kurve – die kein Kreis ist! – tatsächlich gezeichnet wurde. Es reicht offensichtlich nicht, einfach zu verlangen: „Trage auf jeder einzelnen der unendlichen Kreisfamilie einen entsprechenden Punkt B auf.“ Denn wenn man einzelne Kreise und Punkte nacheinander aufzutragen begänne, erhielte man nie mehr als eine diskrete Menge und gelangte nie zu einer durchgehenden Kurve.3
Andererseits ist es mit ein wenig Findigkeit möglich, einen relativ einfachen physikalischen Mechanismus zu entwerfen, mit dem sich die gewünschte Kurve als Produkt der Bewegung von P auf dem Umfang des ursprünglichen Kreises aufzeichnen läßt. Diese Methode ähnelt der Taktik des Nikomedes, der eine mechanisch erzeugte Kurve, die sogenannte Konchoide, benutze, um einen Würfel zu verdoppeln.
Zurück zu Archytas
Von diesem Standpunkt läßt sich der einzigartige Durchbruch von Archytas besser würdigen, der weit über die obigen „Ad-hoc-Methoden“ hinausging. Er entdeckte einen höheren Lösungsansatz für das Problem, womit er über zwei Jahrtausende vor Gauß dessen Begründung der komplexen Zahlen 1799 vorwegnahm.
Ausgehend von dem ursprünglichen Kreis mit dem Durchmesser OA verwendet Archytas einen neuen Bewegungsgrad, um einen Torus zu erzeugen. Dadurch führt uns Archytas in gewisser Weise in ein ganz neues Universum. Anstatt nämlich die Lösung „von unten nach oben“ anzugehen, wie wir es oben versucht haben, kann man nunmehr „von oben nach unten“ vorgehen.
Man erhält den fraglichen Torus, indem man den Ausgangskreis (vom Durchmesser OA = 2) zuerst in die senkrechte Ebene (bei festem OA) und dann den sich ergebenen vertikalen Kreis um die senkrechte Achse durch O dreht. An jedem Punkt P auf dem Torus ist der senkrechte Querschnitt durch die Torusachse ein Kreis mit dem Durchmesser 2; wenn Q die Projektion von P auf den horizontalen Durchmesser dieses Kreises bezeichnet, gilt das Verhältnis OQ : OP = OP : 2 – jetzt als invariante Beziehung für die gesamte Fläche des Torus (Abbildung 3 a–c).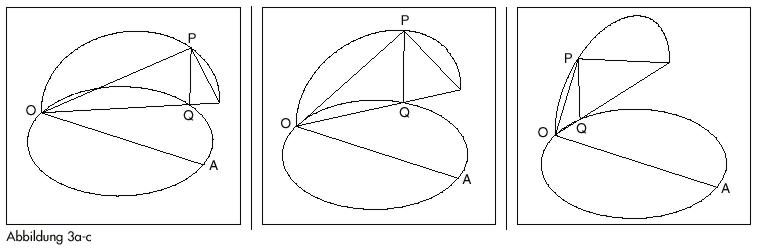
Man beachte, daß Q in der waagerechten Ebene des ursprünglichen Kreises liegt und mit der senkrechten Projektion von P auf diese Ebene übereinstimmt.
Jetzt lassen sich leicht weitere Drehungsgrade anwenden, um andere harmonische Beziehungen herzustellen. Ein Weg, den Archytas für seine Lösung wählte, besteht darin, den Torus mit dem senkrechten Zylinder, dessen Basis aus dem Ausgangskreis mit dem Durchmesser OA (oder Länge 2) besteht, zu schneiden. Jeder Punkt P, der auf der Schnittfläche von Torus und Zylinder liegt, gehört automatisch zwei Kreisen an:
- dem senkrechten Torusquerschnitt durch P, der, wie bereits erwähnt, die Beziehung OQ : OP = OP : 2 entstehen läßt, und
- dem waagerechten Querschnitt des Zylinders bei P (Abbildung 4)

Wenn man den Querschnitt des Zylinders auf die ursprüngliche waagerechte Ebene projiziert, bildet sich P auf dem bereits erwähnten Punkt Q ab, und der Zylinderquerschnitt projiziert sich auf den ursprünglichen Kreis in der Ebene mit Q auf seinem Umfang. Nun können wir mit Q so verfahren, wie früher mit P: Q erzeugt im ursprünglichen Kreis eine zweite Serie harmonischer Beziehungen der Form OR : OQ = OQ : 2 , wobei R die Projektion von Q auf OA ist (Abbildung 5 a–c).
Zur Erinnerung: Wir versuchen ein Ereignis zu erzeugen, für das die Beziehung 1:OQ = OQ:OP zutrifft. Wäre es mit einem dritten Erzeugungsgrad möglich, OR mit OP in einer Weise zu verbinden, daß sich letztere Beziehung automatisch aus der ersteren ergibt?
Man beachte zunächst, daß OR : OQ = OQ : 2 der Umkehrbeziehung 2 : OQ = OQ : OR entspricht. Was sagt das über die Beziehung 1 : OQ ? Offenbar ist der Proportionalitätsfaktor, der erforderlich ist, um die Einheitslänge 1 in die Länge OQ zu transformieren, doppelt so groß wie der Faktor, der 2 in OQ transformiert. Wendet man diesen doppelten Faktor auf OQ an, ergibt sich 2 ∙ OR anstatt OR. Somit wird aus 2 : OQ = OQ : OR das Verhältnis:
1 : OQ = OQ : (2 · OR)
Um das gewünschte Verhältnis 1 : OQ = OQ : OP zu bekommen, müßte OP gleich 2 · OR sein. Welche Art Ereignis zusätzlich zu den anderen würde diese Beziehung erzeugen?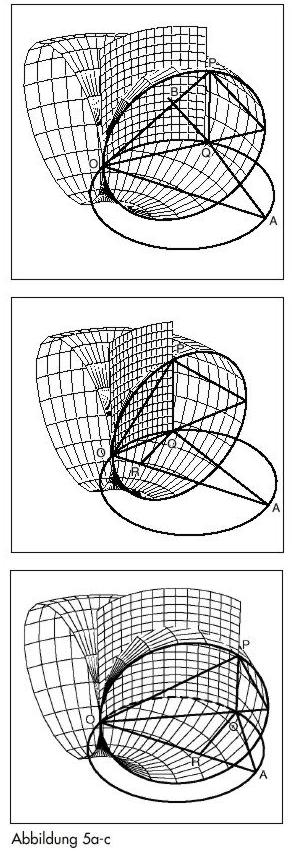
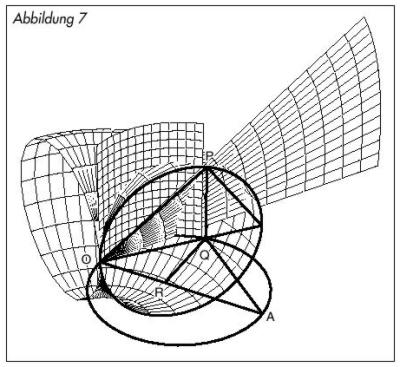
Betrachten wir, wie OP und OR in unserer Konstruktion bisher miteinander in Beziehung standen. Ganz einfach: R ist sowohl die Projektion von Q auf OA als auch die direkte senkrechte Projektion von P auf die Achse OA, d. h. den Punkt, an dem die Ebene P, senkrecht zu der Achse OA gezeichnet, diese Achse schneidet. Ungeachtet der anderen Einschränkungen für P bedeutet die Bedingung, daß OP zweimal OR sei, nichts anderes, als daß P auf einem bestimmten Kegel mit der Spitze O und der Achse OA liegt (Abbildung 6). Der gesuchte Kegel läßt sich leicht konstruieren; das ist wiederum der vorläufige Schritt, den Eudemus beschreibt. Das gewünschte Ereignis ist somit der dreifache Schnitt von Torus, Zylinder und Kegel (Abbildung 7).
Damit sind wir bei Archytas‘ Konstruktion angelangt. Diesmal nicht, um sie zu bestätigen, sondern um sie eigenständig zu erzeugen.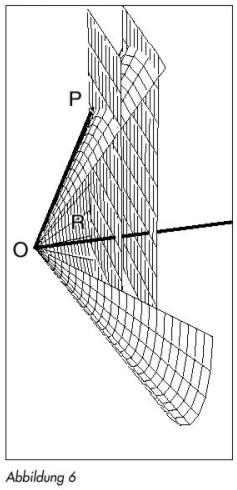
Fußnote(n)
- Die Kettenlinie beispielsweise, die zu ihrer Erzeugung physikalische Substanz erfordert, könnte in der Welt von Descartes, Lagrange und Euler gar nicht existieren![↩]
- Aufmerksame Leser werden hier bereits Andeutungen von Kegelprozessen bemerkt haben, die bei Archytas noch deutlicher werden und in ganzer Klarheit dann bei Gauß‘ komplexen Zahlen auftauchen. [↩]
- Aus ähnlichen Gründen kann die Mathematik, wie sie gewöhnlich verstanden wird, keine wirkliche Stetigkeit repräsentieren, sondern bestenfalls bestimmte Ergebnisse eines stetigen Prozesses beschreiben. Nur die Entwicklungsrichtung der Mathematik, wie sie von Leibniz in seiner ursprünglichen Konzeption des Kalküls angelegt und von Riemann fortgesetzt wurde, bietet der Mathematik einen Ausweg, um die Realität stetiger Prozesse im Universum immer angemessener darstellen zu können. Die Frage der Kettenlinie ist hierfür beispielhaft.[↩]