Warum heute immer noch die gleiche fehlerhafte Mathematik in der Tradition Eulers und Lagranges gelehrt wird, die Gauß schon vor zwei Jahrhunderten eindeutig widerlegt hat?
Schüler und Studenten auf der ganzen Welt wird es interessieren zu erfahren, daß das Lehrgebäude der Mathematik, wie es heute an Schulen und Universitäten gelehrt wird, grundlegende Mängel aufweist. Der entscheidende Beweis dafür wurde von einem jungen Studenten namens Carl Friedrich Gauß schon vor über 200 Jahren geführt.
In seiner Doktorarbeit mit dem ersten vollständigen Beweis des Fundamentalsatzes der Algebra 1799 legte Gauß die grundlegenden Irrtümer in den Arbeiten der führenden akademischen Größen seiner Zeit, Leonhard Euler und Jean-Louis Lagrange, offen und demonstrierte die eindeutige Überlegenheit seiner eigenen revolutionären wissenschaftlicher Entdeckungsmethode – eine Methode, die auf Johannes Kepler und Gottfried Wilhelm Leibniz zurückgeht.
Warum, so muß man sich fragen, wird heute in Schulen und Universitäten immer noch die gleiche fehlerhafte Mathematik in der Tradition Eulers und Lagranges gelehrt, die Gauß vor zwei Jahrhunderten so eindeutig widerlegt hat? Kaum etwas anderes enthüllt so offenkundig den Bankrott der derzeit akzeptierten Bildungsnormen und den kläglichen Zustand des herrschenden Systems im allgemeinen. Tatsächlich macht dieser Skandal deutlich, daß unser Bildungssystem auf einem Betrug basiert; es soll jungen Menschen gar nicht beibringen, die Wahrheit zu entdecken! Statt dessen sollen sie als gehorsame Geistes-Sklaven an ein System gefesselt werden, das seinem Untergang zustrebt.
Zum Glück ist jedoch eine neue, revolutionäre politische Kraft entstanden, die sich um diese fundamentalen Probleme unserer Zivilisation kümmern will: Die von Lyndon LaRouche geschaffene internationale Jugendbewegung, die sich vor allem in den USA ausbreitet, aber jetzt auch in Iberoamerika und Europa Fuß faßt. Aus wohlüberlegten Gründen entschloß sich LaRouche, die Denkmethode von Carl Friedrich Gauß hinter dessen Widerlegung der gängigen Lehrbuchmathematik zur Grundlage dieser Bewegung zu machen.
Die Durcharbeitung der gesamten Beweisführung von Gauß’ Arbeit von 1799 erfordert zwar bestimmte fachliche Voraussetzungen, aber die Grundfrage, um die es dabei geht, ist sehr alt und kann von jedem verstanden werden, der sich ernsthaft mit dieser Frage befaßt. Es geht um den Konflikt zwischen zwei diametral entgegengesetzten Zahlenvorstellungen, Vorstellungen, die ihrerseits zwei völlig unterschiedliche Sichten vom Menschen und dem Universum verkörpern.
Auf der einen Seite steht eine weitverbreitete, aber widersinnige Vorstellung, die sich historisch auf die Angriffe des Aristoteles auf Platon zurückverfolgen läßt. Auf der anderen Seite steht die Vorstellung von Pythagoras und Platon, deren eindeutige Überlegenheit Gauß erneut bewies. Sie war jedesmal im Spiel, als in den letzten 2500 Jahren revolutionäre Fortschritte in Mathematik und Physik erzielt worden sind.
Um den Unterschied klar zu machen, wollen wir uns zunächst mit der falschen Konzeption beschäftigen.
Die empiristische Zahlentheorie
Die heutige verbreitete Meinung über „Zahlen“ – wie sie jedem in der Schule beigebracht wird – leitet sich von der unsinnigen Lehre des Aristoteles ab, die später John Locke aufgriff, welche behauptet, daß sämtliche unserer Ideen auf sinnlicher Wahrnehmung beruhen. So wird beispielsweise angenommen, daß die Zahl 2 in prähistorischer Zeit aus dem wiederholten Seheindruck von zwei Bäumen, zwei Steinen, zwei Hunden usw. entstanden sei, woraus sich die 2 als gemeinsames Merkmal herausbildete. Zusammen mit der sich entwickelnden Fertigkeit, Gegenstände zu zählen und Längen, Flächen, Volumen, Gewichte usw. zu messen, soll dieser Abstraktionsvorgang letztlich zum modernen mathematischen Begriff der „realen Zahlen“ geführt haben.
Allein schon die Wahl des Begriffs „reale Zahlen“ drückt auf seiten von Aristoteles, Locke, Euler u. a. die Absicht aus, jeden Zahlenbegriff, der sich nicht letztlich auf das Zählen und Messen greifbarer Gegenstände zurückführen läßt, als „unmöglich“ oder „imaginär“ abzulehnen. So erging es in der Tat den sogenannten negativen Zahlen, die jahrhundertelang als „unmöglich“ galten. Das gleiche wiederholte sich bei der berühmten √–1 (Quadratwurzel von –1), deren physische Realität von Gauß bewiesen wurde, die aber bis auf den heutigen Tag „imaginär“ genannt wird.
Nach Eulers Meinung könnte √–1 in der Realität gar nicht existieren, da damit eine Länge ausgedrückt würde, deren Quadrat kleiner als Null wäre. Offenbar müsse aber die Fläche eines Quadrats immer eine positive Größe sein. Entsprechend sei √–1 „unmöglich“!
Genau dieses Eulersche Argument und die irrige Vorstellung von „Realität“, die dahinter steht, widerlegte der junge Carl Gauß in seiner Arbeit von 1799, und zwar grundlegend.1
Das Problem, um das es hier geht, ist das folgende. Aus unserer Sinneswahrnehmung – oder zumindest dem, was gemeinhin unter Sinneswahrnehmung verstanden wird – scheinen wir schließen zu können, daß das Universum aus einer Vielzahl physischer Gegenstände unterschiedlicher Art, besteht, die sich im Prinzip mittels der sogenannten „realen Zahlen“ zählen und messen lassen. Was wäre aber, wenn sich die wahre Realität des physischen Universums von einer solchen Ansammlung von sich im Raum bewegenden Gegenständen völlig unterscheidet? Was wäre, wenn Atome, Moleküle oder sogenannte „Elementarteilchen“ lediglich Erscheinungen, physische Effekte, sind, die durch einen grundlegenderen Prozeß erzeugt werden? Was wäre, wenn sich herausstellte, daß sich die grundlegenden Erzeugungs- oder Schöpfungsprozesse im Universum aufgrund ihrer Eigenart gar nicht durch die gewöhnlichen sogenannten „realen Zahlen“ beschreiben lassen, sondern eine ganz andere „Zahlengattung“ erfordern? In diesem Fall müßten wir eine solche Zahlengattung als „real“ betrachten, und gerade nicht die von den Nachfolgern des Aristoteles als „real“ bezeichneten Zahlen.
Daß dem so ist, hat Carl Gauß in seiner Arbeit von 1799 sowie in seiner späteren Beschäftigung mit den sogenannten „komplexen Zahlen“ gezeigt. Unter anderem bewies Gauß die physische Realität von Zahlen wie √–1, die Euler und Lagrange als „imaginär“ abgetan hatten.
Platon und die „Potenzzahlen“
Um Gauß‘ Argumentation wirklich zu verstehen, muß man zunächst etwas von dem zweiten, pythagoräisch-platonischen Zahlenbegriff begriffen haben, der dem von Aristoteles und Euler diametral entgegengesetzt ist.
Im pythagoräisch-platonischen Denken kommen Zahlen nicht von Sinneswahrnehmungen; sie bilden vielmehr im Geist eine besondere Art Idee. Das Wesen solcher Ideen ist es, daß sie der menschlichen Vernunft zumindest indirekt eine wachsende Kraft über das sichtbare Universum verleihen.
Diese Vorstellung mag vielen Lesern, die nur mit dem aristotelischen Zahlenbegriff vertraut sind, merkwürdig und ungewohnt erscheinen, aber sie läßt sich mit Hilfe einer berühmten Problemstellung der klassischen griechischen Geometrie, die in dem Prozeß zu Gauß‘ Arbeit von 1799 eine entscheidende Rolle spielte, einfach verstehen: der Verdoppelung einer Geraden, der Verdoppelung eines Quadrats und der Verdoppelung eines Würfels.
I. Man stelle sich eine gegebene Gerade AB vor. Wie kann man eine Gerade konstruieren, die genau die doppelte Länge der gegebenen hat? Mit Hilfe der Methoden der klassischen griechischen Geometrie läßt sich das leicht lösen (Abbildung 1): Man muß nur mit einem Zirkel einen Kreis mit dem Radius AB um B schlagen; dann verlängert man die Strecke AB mit einem Lineal über B hinaus, bis diese den Kreis bei C erneut schneidet. Dann ist AC genau doppelt so lang wie AB. Auf ähnliche Weise läßt sich eine gegebene Strecke mit Lineal und Zirkel nach beliebigen ganzzahligen Proportionen vervielfachen oder teilen.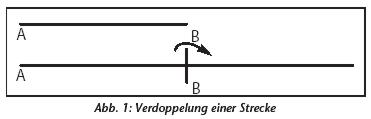
In diesem Fall ist die Lösung zwar sehr leicht, aber man beachte, daß man dabei aus der kleinen eindimensionalen „Welt“ der Strecke selbst heraustreten muß: Eine Drehung (beim Schlagen des Kreises um B) ist erforderlich.
II. Das nächste Problem, mit dem sich Platon in den berühmten Dialogen Menon und Theaitet beschäftigt hat, ist die Verdoppelung eines Quadrats, d. h. es soll ein Quadrat konstruiert werden, dessen Fläche doppelt so groß ist wie das Ausgangsquadrat. Hier ist die Lösung keineswegs so offensichtlich wie bei der Verdoppelung des Streckenabschnitts. Wenn man z. B. die Seiten des Quadrats verdoppelt, erhält man ein Quadrat, das viermal und nicht zweimal so groß ist wie die Ausgangsfläche. Welche Seitenlänge ergibt genau die doppelte Fläche?
Einige zusätzliche Überlegungen sind erforderlich, die über die bisherigen hinausgehen. Im Menon bringt Sokrates einen ungebildeten Sklavenjungen nur durch Fragestellungen dazu, die Lösung zu entdecken, wie sie in Abbildung 2 dargestellt ist. Die doppelte Quadratfläche wird erzeugt, indem man die Diagonalen der vier sich ergebenen Quadrate zeichnet. Man beachte, daß die Diagonale und das darauf konstruierte Quadrat gegenüber dem Ausgangsquadrat um 45 Grad gedreht ist.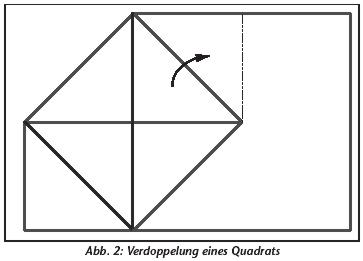
An dieser Stelle wird der charakteristische Unterschied zwischen den beiden Zahlenbegriffen besonders deutlich. Vom Standpunkt der „realen Zahlen“ von Euler und Aristoteles ist die Diagonale eine Länge wie jede andere. Vom Standpunkt des Pythagoras und Platon verkörpert die Erzeugung der Diagonalen jedoch eine höhere Potenz („Kraft“) als die vorherige Konstruktion. Die Verdoppelung des Quadrats erfordert demnach eine zusätzliche Entdeckung, deren Idee sich weder auf einfache logische Weise aus der Problemstellung als solcher noch aus der Lösung des früheren Problems (I) ableiten läßt. Dieser Umstand wurde noch durch einen den Anhängern des Pythagoras zugeschriebenen Beweis unterstrichen, daß die Länge der Diagonale eines Quadrats nicht zu der gleichen Klasse von Längen gehört, die sich durch bloße Multiplikation oder Division der Ausgangsseite nach ganzzahligen Proportionen erzeugen läßt (d. h. Diagonale und Seite sind „inkommensurabel“).
III. Das Problem, einen Würfel zu verdoppeln, gehört zu den berühmtesten der klassischen griechischen Geometrie. Erneut stellt sich das Paradox, daß man die Methode der Verdoppelung des Quadrats nicht einfach auf die Verdoppelung des Würfels anwenden kann. Es stellt sich in der Tat heraus, daß man die Seite eines Würfels mit dem doppelten Volumen eines Ausgangswürfels mit Zirkel und Lineal gar nicht konstruieren kann. Die Lösungen, die Platons Freund Archytas und andere griechische Geometer entwickelten, gründen sich auf ganz unterschiedliche Überlegungen und Methoden als die unter I. und II. angewendeten Konstruktionen. Die Konstruktion des Archytas (Abbildung 3) erzeugt die gewünschte Seitenlänge durch den Schnitt dreier Flächen im Raum, die jeweils wiederum durch Drehungen erzeugt werden: Torus, Zylinder und Kegel! Aus Platzgründen können die Prinzipien von Archytas‘ brillanter Konstruktion hier nicht ausgeführt werden, aber es sollte deutlich werden, daß sie wiederum eine höhere „Kraft“ als die beiden vorhergehenden darstellen.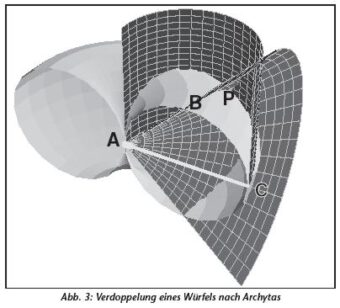
Betrachten wir nun die drei Konstruktionen als geordnete Reihe: Der Prozeß der Verdoppelung von Linie, Quadrat und Würfel. Man halte fest:
- Jede Lösung hängt von Überlegungen ab, die den ursprünglichen Rahmen sprengen, in dem das Problem gestellt wurde.
- Jede Lösung hängt von Prinzipien ab, die über jene hinausgehen, die für das vorherige Problem angemessen waren.
- Die Rotationswirkung ist ein gemeinsames charakteristisches Merkmal aller drei Konstruktionen.
Nimmt man diese drei Aspekte zusammen, ergibt sich eine erste Annäherung des pythagoräisch-platonischen Begriffs einer geordneten, der Potenz (der „Kraft“) nach ansteigenden Reihe. Das ist der zentrale Ausgangspunkt für Gauß‘ Entdeckungen. Ist es nicht ein Verbrechen, daß diese Reihe im normalem Mathematikunterricht nicht einmal erwähnt wird?
Der Ursprung der Algebra
Wie Gauß‘ Lehrer Abraham Kästner in seiner unübertroffenen Geschichte der Mathematik schrieb, entwickelte sich aus dem Wunsch nach der Erforschung dieser „höheren Potenzen“ später das, was wir heute „Algebra“ nennen – angefangen mit der islamischen Renaissance. Der Begriff „Algebra“ selbst stammt von dem arabischen Wort Al Jabr her, was soviel wie „Vervollständigung“ oder „Heilung“ bedeutet; in seinem berühmten Buch Hisab Al Jabr w’al Muqalaba (Buch über die Vervollständigung und Ausgleichung) zeigte der große Bagdader Astronom und Mathematiker Al Khwarizmi (780–850) erstmals Methoden zur Aufstellung und Berechnung von Gleichungen zur Lösung geometrischer Probleme. Später benutzte man für die unbekannten Größen, die Al Khwarizmi noch in Worten beschrieben hatte, Buchstaben in den Gleichungen. In dieser formellen Welt der Algebra oder „Buchstabenrechnung“ führt beispielsweise das Problem der Verdoppelung des Quadrats zu der Gleichung:
x · x = 2 oder x2 = 2
Wenn wir die Seite des Ursprungsquadrats als Längeneinheit und seine Fläche als Flächenmaß nehmen und die Größe der Seite eines anderen Quadrats – als Proportion oder Vielfaches dieser Einheit – durch den Buchstaben x ausdrücken, wird die Fläche des zweiten Quadrats x mal x oder x2 sein. Wenn das zweite Quadrat die doppelte Fläche des ersten Quadrats haben soll, dann muß x2 = 2 ergeben. In gleicher Weise führt das Problem der Verdoppelung des Würfels zu der Gleichung:
x · x · x = 2 ,
da das Volumen eines Würfels der Seitenlänge x gleich x · x · x ist, was man auch x3 schreiben kann.
Die formale Analogie zwischen den beiden Gleichungen x2 = 2 und x3 = 2 verschleiert die schon erwähnte Tatsache, daß ihre Lösungen ganz verschiedene geometrische Methoden oder „Potenzen“ erfordern. Diese Diskrepanz zwischen der formalen Algebra und der Wirklichkeit nahm mit der Zeit monströse Ausmaße an, als Descartes und später Euler und Lagrange aus der Algebra ein „vollständiges“ mathematisches System zu machen und alle Geometrie und letztlich sogar die Physik der algebraischen Mathematik unterzuordnen versuchten. Im Vorwort zu seiner berühmten Mechanique analytique von 1788 schrieb Lagrange: „Sie werden in diesem Werk keine Diagramme finden. Die Methode, die ich präsentiere, erfordert weder Konstruktionen noch geometrische oder mechanische Begründungen, sondern nur algebraische Operationen, die in regelmäßiger und einheitlicher Weise durchgeführt werden. Wer die Analysis liebt, wird mit Freude bemerken, wie die Mechanik auf diese Weise eine ihrer Zweige wird, und wird mir dankbar sein, daß ich den Bereich der Analysis auf diese Weise erweitert habe.“
Es war dann Gauß, der 1799 demonstrierte, daß dieser Ansatz sogar im Bereich der Algebra selbst völlig falsch ist! Um darzustellen, wie Gauß das gelang, muß man zunächst etwas mehr darüber sagen, wie Lagrange und Euler versuchten, aus der Algebra ein „vollkommenes“ System zu machen.
Das Lösen von Gleichungen
Schon lange vorher hatten die Mathematiker die Sprache der „Buchstabenrechnung“ durch Einführung bestimmter Symbole erweitert, mit denen man die Quadratwurzel (QWZ), die Kubikwurzel (KWZ) etc. bezeichnete. Heute lernen die Algebraschüler beispielsweise: „Die Lösung der Gleichung x · x = 2 lautet x = √2.“ Damit hat man aber eigentlich gar nichts gelöst, denn der Ausdruck „√2“ ist keine Antwort, sondern eine Frage, nämlich nach der Seite des Quadrats mit der Fläche 2 (oder welche Zahl auch immer unter dem Wurzelzeichen steht). Um sie zu finden, braucht man eine geometrische Konstruktion.
Interessanter ist, daß Al Khwarizmi entdeckte, daß sich noch viele andere Probleme darauf reduzieren lassen, Quadratwurzeln zu finden. So stellte er beispielsweise die Aufgabe: „Finde ein Quadrat, das, wenn man das Zehnfache seiner Seite hinzufügt, 39 ergibt.“ In algebraischer Sprache ausgedrückt hat das Problem die Form der Gleichung:
Al Khwarizmi selbst kam auf die heute übliche Methode zur Lösung solcher Gleichungen, man nennt sie „Vervollständigung des Quadrats“ (Abbildung 4). Sie führt zu einer allgemeinen „Formel“ zur Lösung aller Gleichungen dieses Typs:
x2 + b * x + c = 0
(im genannten Fall ist b = 10 und c = 39), wobei b und c beliebige Größen sind.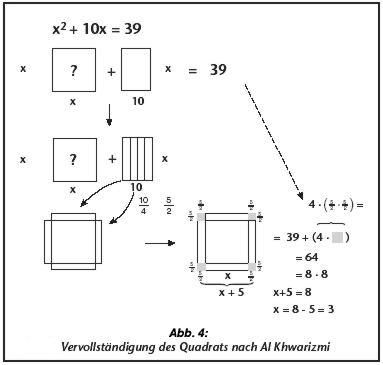
Die „Formel“ für die Lösung – die vielleicht auf den ersten Blick seltsam anmutet, die sich aber aus einer einfachen geometrischen Konstruktion ergibt – lautet:
x = 1/2 (– b +/– √(b2 – 4c)
Um den Wert für x zu finden, müssen wir wieder die Quadratwurzel finden. In dem genannten konkreten Beispiel ergibt die Formel x = 1/2 (– 10 + √(100 + 156)), was 3 ergibt, und das ist tatsächlich die Lösung des ursprünglichen Problems.
In ähnlicher Weise führten die Algebraiker ein Symbol für die „Kubikwurzel“ ein. „KWZ 2″ beispielsweise bedeutet „die Seite eines Würfels, dessen Volumen 2 ist“, oder in anderen Worten die Lösung der Gleichung x3 = 2. Wie wir oben festgestellt haben, braucht man eine umfangreiche Konstruktion, um den tatsächlichen Wert für die „Kubikwurzel“ von 2 oder irgendeiner anderen Zahl zu finden. Aber sobald wir einmal wissen, wie das geht, können wir praktisch jedes Problem mit einer Mischung von Würfeln, Quadraten und Vielfachen einer unbekannten Größe lösen. Tatsächlich haben die italienischen Geometer Tartaglia und Cardan im 16. Jahrhundert eine allgemeine Formel für die Lösung einer Gleichung dieser Art entwickelt:
Cardans Formel enthält sowohl Kubikwurzeln als auch Quadratwurzeln und ist beträchtlich komplizierter als Al Khwarizmis Formel (Abbildung 5). Später entdeckte Ferrari eine noch kompliziertere Formel zur Lösung aller Gleichungen „vierten Grades“, d. h. Gleichungen mit x4, x3, x2 und x.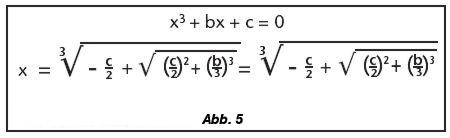
Die Algebra wird zum Imperium
Diese Entwicklungen in der Algebra oder „Buchstabenrechnung“ waren an sich nützlich, aber das formale Rechnen mit Gleichungen verschleierte tendenziell die Geometrie und damit implizit auch die Physik, welche die Realität der Längen, Flächen, Volumen usw. und deren Beziehungen bestimmen. Descartes beispielsweise schlug vor, jedes Problem der Geometrie in Algebra zu „übersetzen“, indem man einen beliebigen Punkt auf einer Ebene durch seine Koordinaten x und y, oder einen beliebigen Punkt im Raum durch seine Koordinaten x, y und z und die verschiedenen geometrischen Formen (Linien, Kreise, Ebenen, Oberflächen, Körper etc.) durch Gleichungen darstellt, in denen diese Koordinaten als unbekannte oder variable Größen enthalten sind. Unter der Rubrik der „analytischen Geometrie“ wurden und werden damit Generationen von Schülern gequält. Sie lernen beispielsweise, daß die Gleichung
x2 + y2 = 1
einen Kreis mit dem Radius 1 um den Ursprung (x = 0 , y = 0) einer Ebene beschreibt. Diese Gleichung ist aus dem Satz des Pythagoras abgeleitet und entspricht der Aussage, daß der Punkt (x,y) den Abstand 1 vom Punkt (0,0) hat.
Aber hier stellt sich ein schrecklicher Fehler ein: Wenn man in den modernen Lehrbüchern Descartes nachfolgend versucht, einen Kreis durch diese Gleichung zu definieren – indem man z. B. sagt, der Kreis sei die Menge aller Punkte (x,y), für die die oben aufgestellte Gleichung gilt – dann unterschlägt man völlig die reale physische Wirkung, die Kreise erzeugt: die Rotation!
Tatsächlich können Algebra und formale Mathematik Dinge wie Bewegung, Änderung oder Wirkung, also die entscheidenden Dinge im realen Universum, nicht ausdrücken. Doch Euler und Lagrange ignorierten dies und betrieben fanatisch ihren Versuch, aus der Algebra ein alles umfassendes „mathematisches Imperium“ zu machen, in dem man alle Probleme lösen kann.
Insbesondere glaubten sie, es müsse zur Lösung jeder beliebigen algebraischen Gleichung formale Ausdrücke oder Formeln geben – analog zu den Formeln von Al Khwarizmi, Cardan-Tartaglia und Ferrari für Gleichungen zweiten, dritten und vierten Grades. Sie dachten, dazu müsse man nur die Methoden der formalen algebraischen Rechnung, die in diesen Fällen ausreichend schien, weiter ausarbeiten.
Das Märchen der „imaginären Zahlen“
Es war aber schon vor Gauß‘ vernichtender Kritik deutlich geworden, daß die Algebra voller Paradoxe und Anomalien steckt; vor allem tauchten in den Formeln zur Lösung algebraischer Gleichungen immer wieder sogenannte „imaginäre Zahlen“ auf. Betrachten wir beispielsweise die Gleichung
x2 + 1 = 0 , oder anders ausgedrückt x2 = –1 .
Die „Lösung“ wäre nach den Begriffen der formalen Algebra x = √–1. Aber was bedeutet das? Ihrer Natur nach sind Längen, Flächen oder Volumen immer entweder Null oder eine positive Größe. Es kann also kein Quadrat der Fläche – 1 geben, und somit auch keine Quadratwurzel von – 1, jedenfalls nicht, solange man unter „Zahl“ etwas versteht, was aus dem Zählen oder Messen sichtbarer Größen abgeleitet ist.
Aus diesem Grund bezeichnete man bis zur Zeit von Euler und Lagrange die Gleichung x2 + 1 = 0 gewöhnlich als „unmögliche Gleichung“, da x2 + 1 offensichtlich immer größer oder gleich 1 sein mußte, und √–1 nannte man eine „unmögliche“ oder „imaginäre“ Zahl, die aus der Mathematik ausgeklammert werden sollte.
Diese „Apartheid“ konnte jedoch nur funktionieren, solange man den Bereich der „unmöglichen“ Gleichungen und „imaginären“ Zahlen und den der „möglichen“ Gleichungen und „reellen“ Zahlen total voneinander trennen konnte. Diese klare Trennung erwies sich jedoch bereits bei der Cardanschen Formel zur Lösung von Gleichungen dritten Grades als unmöglich. So schrieb Cardan bereits 1539 an seinen Kollegen Tartaglia, die Gleichung x3 = 15x + 4 habe zwar die völlig „reale“ Lösung x = 4 , der formale Ausdruck für diese Lösung nach der allgemeinen Formel, die er und seine Kollegen entwickelt hatten, enthalte aber die „imaginäre Zahl“ √(–124). Dieses Phänomen wurde als „Cardans Paradox“ bekannt. Viele Mathematiker wie Newton und Euler versuchten dann eine andere Formel ohne diesen unangenehmen Mangel der Cardanschen Formel zu finden – ohne Erfolg: Immer wieder tauchten in den Formeln zur Lösung von Gleichungen, die völlig „reale“ Lösungen hatten, „imaginäre Zahlen“ auf!
In einem Versuch des „Krisenmanagements“ schuf Euler die folgende „Sprachregelung“: Ausdrücke wie √–1 sind unmöglich und ohne Bedeutung in der realen Welt; aber man soll sie trotzdem in der Algebra als unverzichtbare, doch sonst bedeutungslose formale Symbole zulassen, mit denen man nach bestimmten Regeln rechnen kann. Euler sagte damit praktisch, was seither den armen Schülern immer wieder erklärt wird: „Fragt nicht, was √–1 bedeutet. Seid still und lernt, wie man damit rechnet, dann besteht ihr die Prüfung!“
Genauso wie bei Staatsmännern in Krisenzeiten zeigt sich erst genau dann, wenn ein scheinbar unlösbares Paradox auftritt, wie gut ein Wissenschaftler denken kann. Während Euler und andere versuchten, das Problem mit sophistischen Tricks unter den Teppich zu kehren, suchte der junge Carl Gauß die Wahrheit.
Fußnote(n)
- Der Fehler, der Eulers Denken zugrundeliegt, wurde bereits von Gauß‘ Lehrer Abraham Kästner in dessen Vorwort zur ersten Veröffentlichung von Leibniz‘ philosophischen Schriften 1764 erwähnt. Kästner beginnt mit den Worten: „Daß das wirkliche Universum ganz anders ist als das scheinbare, ist eine Wahrheit, die nicht länger in Zweifel gezogen werden sollte.“[↩]
